Batch Normalization

概念

Batch Normalization：批标准化
批：一批数据，通常为mini-batch
标准化：0均值，1方差

参考文献：《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》
文中提出了BN的五个优点：

  1. 可以用更大学习率，加速模型收敛
  2. 可以不用精心设计权值初始化
  3. 可以不用dropout或较小的dropout
  4. 可以不用L2或者较小的weight decay
  5. 可以不用LRN（local response normalization）

计算方式

image.png
注意该算法最后一步，被称作affine transform：它可以让模型更灵活地调整数据的分布。如何调整分布的超参数BN、LN、IN and GN - 图2都是通过模型学习得到的。这样就增强了模型的Capacity。

然而如此简单的BN算法能有上述那么多的优点，其实是无心插柳柳成荫。BN最先被提出来是为了解决Internal Covariate Shift（ICS，数据尺度变化）。

Internal Covariate Shift

该问题在权重初始化章节介绍过，其实就是当权重的方差如果有增大或者缩小的趋势，那么当网络层层数增多时，就会造成梯度爆炸或者梯度消失的问题。

而BN算法一开始就是解决这个问题，只是后面发现它还能带来一系列的好处。

_BatchNorm（基类）

image.png

  • nn.BatchNorm1d
  • nn.BatchNorm2d

  • nn.BatchNorm3d

    基类的参数

  • num_features：一个样本特征数量（最重要）

  • eps：分母修正项，一般是1e-5
  • momentum：指数加权平均估计当前mean/var
  • affine：是否需要affine transform，默认是true
  • track_running_stats：是训练状态，还是测试状态
    • 如果是训练状态，会根据每个batch的data采用加权平均计算mean和std
    • 如果是测试状态，则会根据当前的统计信息，固定mean和std

主要属性

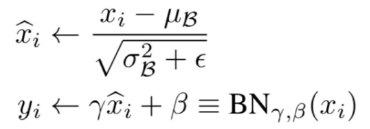
image.png

  • running_mean：均值μ。
    • 计算公式为：running_mean=(1-momentum) pre_running_mean + momentum mean_t
  • running_Var：方差σ
    • 计算公式为：running_var=(1-momentum) pre_running_var + momentum var_t
  • weight：affine transform中的γ（可学习）
  • bias：affine transform中的β（可学习）

注意：这里running_mean和running_Var都是在特征数量的维度上进行计算。即一个特征有多少个特征数量num_features，最后running_mean和running_Var的长度就有多少。

举个例子理解running_mean和running_Var的加权平均计算：
构造数据tensor([[[1.], [2.], [3.], [4.], [5.]],
[[1.], [2.], [3.], [4.], [5.]],
[[1.], [2.], [3.], [4.], [5.]]])
假设初始化时参数是0均值1标准差，
则在iteration0时，第2个特征的running_mean = (1-0.3)0+0.32=0.6
running_Var = (1-0.3)1+0.30=0.7
在iteration1时，第2个特征的running_mean = (1-0.3)0.6+0.32=1.02
running_Var = (1-0.3)0.7+0.30=0.49
running_Var同理。

代码实现

  1. class MLP(nn.Module):
  2.     def __init__(self, neural_num, layers=100):
  3.         super(MLP, self).__init__()
  4.         self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
  5.         self.bns = nn.ModuleList([nn.BatchNorm1d(neural_num) for i in range(layers)])
  6.         self.neural_num = neural_num
  8.     def forward(self, x):
  10.         for (i, linear), bn in zip(enumerate(self.linears), self.bns):
  11.             x = linear(x)
  12.             x = bn(x)
  13.             x = torch.relu(x)
  15.             if torch.isnan(x.std()):
  16.                 print("output is nan in {} layers".format(i))
  17.                 break
  19.             print("layers:{}, std:{}".format(i, x.std().item()))
  21.         return x
  23.     def initialize(self):
  24.         for m in self.modules():
  25.             if isinstance(m, nn.Linear):
  27.                 # method 1
  28.                 # nn.init.normal_(m.weight.data, std=1)    # normal: mean=0, std=1
  30.                 # method 2 kaiming
  31.                 nn.init.kaiming_normal_(m.weight.data)
  34. neural_nums = 256
  35. layer_nums = 100
  36. batch_size = 16
  38. net = MLP(neural_nums, layer_nums)
  39. # net.initialize()
  41. inputs = torch.randn((batch_size, neural_nums))  # normal: mean=0, std=1
  43. output = net(inputs)
  44. print(output)

通过实验发现：当单独使用BN时，参数就能保持在很好的尺度，所以不需要精心设计权重初始化，例如使用Kaiming初始化等方法。

nn.BatchNorm1d

input = Bs 特征数 1d特征

nn.BatchNorm2d

input = Bs 特征数 2d特征
**

nn.BatchNorm3d

input = Bs 特征数 3d特征
**

代码示例

  1.     batch_size = 3
  2.     num_features = 4
  3.     momentum = 0.3
  5.     features_shape = (2, 2, 3)
  7.     feature = torch.ones(features_shape)                                                # 3D
  8.     feature_map = torch.stack([feature * (i + 1) for i in range(num_features)], dim=0)  # 4D
  9.     feature_maps = torch.stack([feature_map for i in range(batch_size)], dim=0)         # 5D
  11.     print("input data:\n{} shape is {}".format(feature_maps, feature_maps.shape))
  13.     bn = nn.BatchNorm3d(num_features=num_features, momentum=momentum)
  15.     running_mean, running_var = 0, 1
  17.     for i in range(2):
  18.         outputs = bn(feature_maps)
  20.         print("\niter:{}, running_mean.shape: {}".format(i, bn.running_mean.shape))
  21.         print("iter:{}, running_var.shape: {}".format(i, bn.running_var.shape))
  23.         print("iter:{}, weight.shape: {}".format(i, bn.weight.shape))
  24.         print("iter:{}, bias.shape: {}".format(i, bn.bias.shape))

这里构造了一个shape为torch.size([3，4，3，2，2])的input，运行结果为：
image.png
即对数据的特征维度，每个特征分别计算一组running_mean，running_Var，weight和bias。

Layer Normalization（LN）

起因：BN不适用于变长的网络，如RNN，网络层神经元个数每次不一样。
思路：逐层计算均值和方差

注意事项：

  1. 不再有running_mean和running_var
  2. gamma和beta为逐元素计算的，即每个神经元都计算一组BN、LN、IN and GN - 图6

nn.LayerNorm

image.png
主要参数：

  • normalized_shape：该层特征形状（最重要）
  • eps：分母修正项（公式里面的ϵ）
  • elementwise_affine：是否需要逐元素的affine transform

参考文献：《Layer Normalization》

代码实现

  1.     batch_size = 2
  2.     num_features = 3
  4.     features_shape = (2, 2)
  6.     feature_map = torch.ones(features_shape)  # 2D
  7.     feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0)  # 3D
  8.     feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0)  # 4D
  10.     # feature_maps_bs shape is [2, 3, 2, 2],  B * C * H * W
  11.     ln = nn.LayerNorm(feature_maps_bs.size()[1:], elementwise_affine=True)
  12.     # ln = nn.LayerNorm(feature_maps_bs.size()[1:], elementwise_affine=False)
  13.     # ln = nn.LayerNorm([3, 2, 2])
  15.     output = ln(feature_maps_bs)
  17.     print("Layer Normalization")
  18.     print(ln.weight.shape)
  19.     print(feature_maps_bs[0, ...])
  20.     print(output[0, ...])

注意在输入LayerNorm的参数normalized_shape时，可以用input.size()[1: ]来取，得到C H W

Instance Normalization

起因：在图像生成任务中（如下图），每个batch的风格是不一样的，把不同batch的特征来求均值明显是不好的。所以BN在图像生成（lmage Generation）中不适用。
image.png

思路：我们认为数据的每个channel的风格是不同的，所以这里逐Instance（channel）计算均值和方差
参考文献：

  1. 《Instance Normalization:The Missing Ingredient for Fast Stylization》
  2. 《Image Style Transfer Using Convolutional Neural Networks》

nn.InstanceNorm

image.png
主要参数：（和bn一样，InstanceNorm也有1d，2d，3d，这里就不赘述了）：

  • num_features：一个样本特征数量（最重要）
  • eps：分母修正项
  • momentum：指数加权平均估计当前mean/var
  • affine：是否需要affine transform
  • track_running_stats：是训练状态，还是测试状态

代码实现

  1.     batch_size = 3
  2.     num_features = 3
  3.     momentum = 0.3
  5.     features_shape = (2, 2)
  7.     feature_map = torch.ones(features_shape)    # 2D
  8.     feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0)  # 3D
  9.     feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0)  # 4D
  11.     print("Instance Normalization")
  12.     print("input data:\n{} shape is {}".format(feature_maps_bs, feature_maps_bs.shape))
  14.     instance_n = nn.InstanceNorm2d(num_features=num_features, momentum=momentum)
  16.     for i in range(1):
  17.         outputs = instance_n(feature_maps_bs)
  19.         print(outputs)

Group Normalization

起因：大模型在训练时会占用很多内存，这时batchsize只能设置很小。然而在小batch样本中，BN估计的值不准。
思路：数据不够，通道来凑。
例如，假设特征数有256个，就将一个样本的256个feature map分为两组，每组128个feature map。然后对每组计算一个均值和标准差。

注意事项（与LN类似）：

  1. 不再有running_mean和running_var
  2. gamma和beta为逐通道（channel）的

应用场景：大模型（小batch size）任务
参考文献：《Group Normalization》

nn.GroupNorm

image.png
主要参数：

  • num_groups：分组数，通常为2.4.8.16.32
  • num_channels：通道数（特征数），如果通道数（特征数）为256，分组数为4，那么每组的通道数为：64
  • eps：分母修正项
  • affine：是否需要affine transform

代码实现

  1.     batch_size = 2
  2.     num_features = 4
  3.     num_groups = 3   # 3 Expected number of channels in input to be divisible by num_groups
  5.     features_shape = (2, 2)
  7.     feature_map = torch.ones(features_shape)    # 2D
  8.     feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0)  # 3D
  9.     feature_maps_bs = torch.stack([feature_maps * (i + 1) for i in range(batch_size)], dim=0)  # 4D
  11.     gn = nn.GroupNorm(num_groups, num_features)
  12.     outputs = gn(feature_maps_bs)
  14.     print("Group Normalization")
  15.     print(gn.weight.shape)
  16.     print(outputs[0])