集合 - HashMap 面试常见的6连问 - 《Java 面试题整理》

问题 1：table 的初始化
- table 的初始化时机是什么时候
问题 2 ：table 的扩容
问题 3、4 ：2 的 n 次幂
- table 的 length 为什么是 2 的 n 次幂
- 求索引的时候为什么是：h&(length-1)，而不是 h&length，更不是 h%length
问题 5：指定 initialCapacity
- Map map = new HashMap(1000); 当存入多少个元素时会触发map的扩容
- Map map1 = new HashMap(10000); 存入第 10001个元素时会触发 map1 扩容吗
问题6：加载因子
总结

Java HashMap
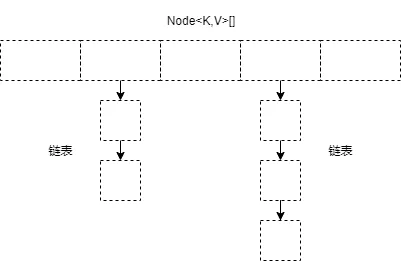
JDK1.8 中 HashMap 的底层实现，底层数据结构数组 + 链表（或红黑树），源码如下

/**  
 * 数组  
 */  
transient Node<K,V>[] table;  
/**  
 * 链表结构  
 */  
static class Node<K,V> implements Map.Entry<K,V> {  
    final int hash;  
    final K key;  
    V value;  
    Node<K,V> next;  
    Node(int hash, K key, V value, Node<K,V> next) {  
        this.hash = hash;  
        this.key = key;  
        this.value = value;  
        this.next = next;  
    }  
    public final K getKey()        { return key; }  
    public final V getValue()      { return value; }  
    public final String toString() { return key + "=" + value; }  
    public final int hashCode() {  
        return Objects.hashCode(key) ^ Objects.hashCode(value);  
    }  
    public final V setValue(V newValue) {  
        V oldValue = value;  
        value = newValue;  
        return oldValue;  
    }  
    public final boolean equals(Object o) {  
        if (o == this)  
            return true;  
        if (o instanceof Map.Entry) {  
            Map.Entry<?,?> e = (Map.Entry<?,?>)o;  
            if (Objects.equals(key, e.getKey()) &&  
                Objects.equals(value, e.getValue()))  
                return true;  
        }  
        return false;  
    }  
}  
/**  
 * 红黑树结构  
 */  
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {  
    TreeNode<K,V> parent;  // red-black tree links  
    TreeNode<K,V> left;  
    TreeNode<K,V> right;  
    TreeNode<K,V> prev;    // needed to unlink next upon deletion  
    boolean red;  
    ...

HashMap 面试常见的6连问 - 图1
但面试往往会问的比较细，例如下面的容量问题，能答上来几个？
1、table 的初始化时机是什么时候，初始化的 table.length 是多少、阀值（threshold）是多少，实际能容下多少元素
2、什么时候触发扩容，扩容之后的 table.length、阀值各是多少？
3、table 的 length 为什么是 2 的 n 次幂
4、求索引的时候为什么是：h&(length-1)，而不是 h&length，更不是 h%length
5、 Map map = new HashMap(1000); 当存入多少个元素时会触发map的扩容；Map map1 = new HashMap(10000); 存入第 10001个元素时会触发 map1 扩容吗
6、为什么加载因子的默认值是 0.75，并且不推荐修改

问题 1：table 的初始化

HashMap 的构造方法有如下 4 种

/**  
 * 构造方法 1  
 *  
 * 通过 指定的 initialCapacity 和 loadFactor 实例化一个空的 HashMap 对象  
 */  
public HashMap(int initialCapacity, float loadFactor) {  
    if (initialCapacity < 0)  
        throw new IllegalArgumentException("Illegal initial capacity: " +  
                                           initialCapacity);  
    if (initialCapacity > MAXIMUM_CAPACITY)  
        initialCapacity = MAXIMUM_CAPACITY;  
    if (loadFactor <= 0 || Float.isNaN(loadFactor))  
        throw new IllegalArgumentException("Illegal load factor: " +  
                                           loadFactor);  
    this.loadFactor = loadFactor;  
    this.threshold = tableSizeFor(initialCapacity);  
}  
/**  
 * 构造方法 2  
 *  
 * 通过指定的 initialCapacity 和 默认的 loadFactor(0.75) 实例化一个空的 HashMap 对象  
 */  
public HashMap(int initialCapacity) {  
    this(initialCapacity, DEFAULT_LOAD_FACTOR);  
}  
/**  
 * 构造方法 3  
 *  
 * 通过默认的 initialCapacity 和 默认的 loadFactor(0.75) 实例化一个空的 HashMap 对象  
 */  
public HashMap() {  
    this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted  
}  
/**  
 *  
 * 构造方法 4  
 * 通过指定的 Map 对象实例化一个 HashMap 对象  
 */  
public HashMap(Map<? extends K, ? extends V> m) {  
    this.loadFactor = DEFAULT_LOAD_FACTOR;  
    putMapEntries(m, false);  
}

构造方式 4 和构造方式 1 实际应用的不多，构造方式 2 直接调用的 1（底层实现完全一致），构造方式 2 和构造方式 3 比较常用，而最常用的是构造方式 3；此时以构造方式 3 为前提来分析，而构造方式 2 则在问题 5 中来分析
使用方式 1 实例化 HashMap 的时候，table 并未进行初始化，那 table 是何时进行初始化的了？平时是如何使用 HashMap 的，先实例化、然后 put、然后进行其他操作，如下

Map<String,Object> map = new HashMap();  
map.put("name", "张三");  
map.put("age", 21);  
// 后续操作  
...

既然实例化的时候未进行 table 的初始化，那是不是在 put 的时候初始化的了，来确认下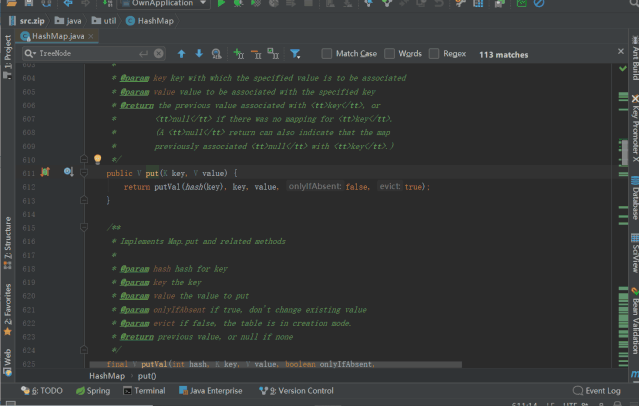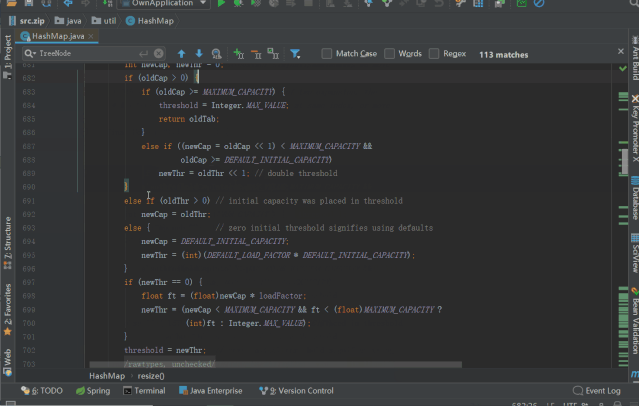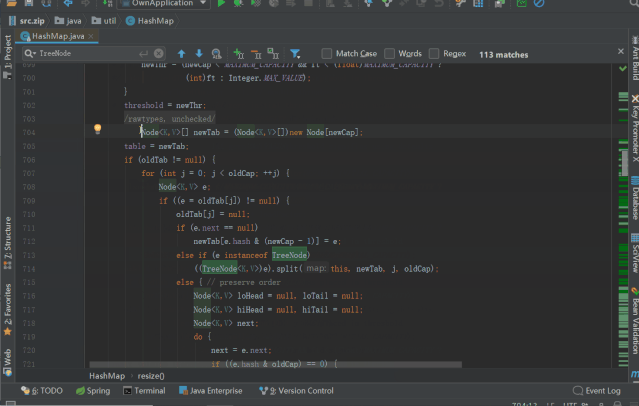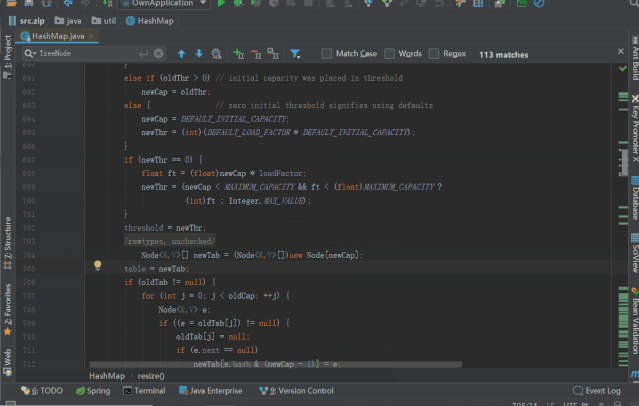
HashMap 面试常见的6连问 - 图2
resize() 初始化 table 或对 table 进行双倍扩容，源码如下（注意看注释）

/**  
 * Initializes or doubles table size.  If null, allocates in  
 * accord with initial capacity target held in field threshold.  
 * Otherwise, because we are using power-of-two expansion, the  
 * elements from each bin must either stay at same index, or move  
 * with a power of two offset in the new table.  
 *  
 * @return the table  
 */  
final Node<K,V>[] resize() {  
    Node<K,V>[] oldTab = table;                    // 第一次 put 的时候，table = null  
    int oldCap = (oldTab == null) ? 0 : oldTab.length; // oldCap = 0  
    int oldThr = threshold;                        // threshold=0, oldThr = 0  
    int newCap, newThr = 0;  
    if (oldCap > 0) {    // 条件不满足，往下走  
        if (oldCap >= MAXIMUM_CAPACITY) {  
            threshold = Integer.MAX_VALUE;  
            return oldTab;  
        }  
        else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&  
                 oldCap >= DEFAULT_INITIAL_CAPACITY)  
            newThr = oldThr << 1; // double threshold  
    }  
    else if (oldThr > 0) // initial capacity was placed in threshold  
        newCap = oldThr;  
    else {               // zero initial threshold signifies using defaults 走到这里，进行默认初始化  
        newCap = DEFAULT_INITIAL_CAPACITY;    // DEFAULT_INITIAL_CAPACITY = 1 << 4 = 16, newCap = 16;  
        newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);    // newThr = 0.75 * 16 = 12;  
    }  
    if (newThr == 0) {    // 条件不满足  
        float ft = (float)newCap * loadFactor;  
        newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?  
                  (int)ft : Integer.MAX_VALUE);  
    }  
    threshold = newThr;        // threshold = 12; 重置阀值为12  
    @SuppressWarnings({"rawtypes","unchecked"})  
        Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];     // 初始化 newTab, length = 16;  
    table = newTab;            // table 初始化完成, length = 16;  
    if (oldTab != null) {    // 此时条件不满足，后续扩容的时候，走此if分支 将数组元素复制到新数组  
        for (int j = 0; j < oldCap; ++j) {  
            Node<K,V> e;  
            if ((e = oldTab[j]) != null) {  
                oldTab[j] = null;  
                if (e.next == null)  
                    newTab[e.hash & (newCap - 1)] = e;  
                else if (e instanceof TreeNode)  
                    ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);  
                else { // preserve order  
                    Node<K,V> loHead = null, loTail = null;  
                    Node<K,V> hiHead = null, hiTail = null;  
                    Node<K,V> next;  
                    do {  
                        next = e.next;  
                        if ((e.hash & oldCap) == 0) {  
                            if (loTail == null)  
                                loHead = e;  
                            else  
                                loTail.next = e;  
                            loTail = e;  
                        }  
                        else {  
                            if (hiTail == null)  
                                hiHead = e;  
                            else  
                                hiTail.next = e;  
                            hiTail = e;  
                        }  
                    } while ((e = next) != null);  
                    if (loTail != null) {  
                        loTail.next = null;  
                        newTab[j] = loHead;  
                    }  
                    if (hiTail != null) {  
                        hiTail.next = null;  
                        newTab[j + oldCap] = hiHead;  
                    }  
                }  
            }  
        }  
    }  
    return newTab;    // 新数组  
}

自此，问题 1 的答案就明了了

table 的初始化时机是什么时候

一般情况下，在第一次 put 的时候，调用 resize 方法进行 table 的初始化（懒初始化，懒加载思想在很多框架中都有应用！）
初始化的 table.length 是多少、阀值（threshold）是多少，实际能容下多少元素

默认情况下，table.length = 16; 指定了 initialCapacity 的情况放到问题 5 中分析
默认情况下，threshold = 12; 指定了 initialCapacity 的情况放到问题 5 中分析

默认情况下，能存放 12 个元素，当存放第 13 个元素后进行扩容

问题 2 ：table 的扩容

putVal 源码如下

/**  
* Implements Map.put and related methods  
*  
* @param hash hash for key  
* @param key the key  
* @param value the value to put  
* @param onlyIfAbsent if true, don't change existing value  
* @param evict if false, the table is in creation mode.  
* @return previous value, or null if none  
*/  
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,  
             boolean evict) {  
  Node<K,V>[] tab; Node<K,V> p; int n, i;  
  if ((tab = table) == null || (n = tab.length) == 0)  
      n = (tab = resize()).length;  
  if ((p = tab[i = (n - 1) & hash]) == null)  
      tab[i] = newNode(hash, key, value, null);  
  else {  
      Node<K,V> e; K k;  
      if (p.hash == hash &&  
          ((k = p.key) == key || (key != null && key.equals(k))))  
          e = p;  
      else if (p instanceof TreeNode)  
          e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);  
      else {  
          for (int binCount = 0; ; ++binCount) {  
              if ((e = p.next) == null) {  
                  p.next = newNode(hash, key, value, null);  
                  if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st  
                      treeifyBin(tab, hash);  
                  break;  
              }  
              if (e.hash == hash &&  
                  ((k = e.key) == key || (key != null && key.equals(k))))  
                  break;  
              p = e;  
          }  
      }  
      if (e != null) { // existing mapping for key  
          V oldValue = e.value;  
          if (!onlyIfAbsent || oldValue == null)  
              e.value = value;  
          afterNodeAccess(e);  
          return oldValue;  
      }  
  }  
  ++modCount;  
  if (++size > threshold)             // 当size（已存放元素个数） > thrshold（阀值），进行扩容  
      resize();  
  afterNodeInsertion(evict);  
  return null;  
}

还是调用 resize() 进行扩容，但与初始化时不同（注意看注释）

/**  
* Initializes or doubles table size.  If null, allocates in  
* accord with initial capacity target held in field threshold.  
* Otherwise, because we are using power-of-two expansion, the  
* elements from each bin must either stay at same index, or move  
* with a power of two offset in the new table.  
*  
* @return the table  
*/  
final Node<K,V>[] resize() {  
  Node<K,V>[] oldTab = table;                    // 此时的 table != null，oldTab 指向旧的 table  
  int oldCap = (oldTab == null) ? 0 : oldTab.length; // oldCap = table.length; 第一次扩容时是 16  
  int oldThr = threshold;                        // threshold=12, oldThr = 12;  
  int newCap, newThr = 0;  
  if (oldCap > 0) {    // 条件满足，走此分支  
      if (oldCap >= MAXIMUM_CAPACITY) {  
          threshold = Integer.MAX_VALUE;  
          return oldTab;  
      }  
      else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&    // oldCap左移一位; newCap = 16 << 1 = 32;  
               oldCap >= DEFAULT_INITIAL_CAPACITY)  
          newThr = oldThr << 1; // double threshold            // newThr = 12 << 1 = 24;  
  }  
  else if (oldThr > 0) // initial capacity was placed in threshold  
      newCap = oldThr;  
  else {               // zero initial threshold signifies using defaults  
      newCap = DEFAULT_INITIAL_CAPACITY;    // DEFAULT_INITIAL_CAPACITY = 1 << 4 = 16, newCap = 16;  
      newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);  
  }  
  if (newThr == 0) {    // 条件不满足  
      float ft = (float)newCap * loadFactor;  
      newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?  
                (int)ft : Integer.MAX_VALUE);  
  }  
  threshold = newThr;        // threshold = newThr = 24; 重置阀值为 24  
  @SuppressWarnings({"rawtypes","unchecked"})  
      Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];     // 初始化 newTab, length = 32;  
  table = newTab;            // table 指向 newTab, length = 32;  
  if (oldTab != null) {    // 扩容后，将 oldTab(旧table) 中的元素移到 newTab（新table）中  
      for (int j = 0; j < oldCap; ++j) {  
          Node<K,V> e;  
          if ((e = oldTab[j]) != null) {  
              oldTab[j] = null;  
              if (e.next == null)  
                  newTab[e.hash & (newCap - 1)] = e;        //   
              else if (e instanceof TreeNode)  
                  ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);  
              else { // preserve order  
                  Node<K,V> loHead = null, loTail = null;  
                  Node<K,V> hiHead = null, hiTail = null;  
                  Node<K,V> next;  
                  do {  
                      next = e.next;  
                      if ((e.hash & oldCap) == 0) {  
                          if (loTail == null)  
                              loHead = e;  
                          else  
                              loTail.next = e;  
                          loTail = e;  
                      }  
                      else {  
                          if (hiTail == null)  
                              hiHead = e;  
                          else  
                              hiTail.next = e;  
                          hiTail = e;  
                      }  
                  } while ((e = next) != null);  
                  if (loTail != null) {  
                      loTail.next = null;  
                      newTab[j] = loHead;  
                  }  
                  if (hiTail != null) {  
                      hiTail.next = null;  
                      newTab[j + oldCap] = hiHead;  
                  }  
              }  
          }  
      }  
  }  
  return newTab;  
}

自此，问题 2 的答案也就清晰了
什么时候触发扩容，扩容之后的 table.length、阀值各是多少

当 size > threshold 的时候进行扩容
扩容之后的 table.length = 旧 table.length * 2,
扩容之后的 threshold = 旧 threshold * 2
问题 3、4 ：2 的 n 次幂
table 是一个数组，那么如何最快的将元素 e 放入数组？当然是找到元素 e 在 table 中对应的位置 index ，然后 table[index] = e; 就好了；如何找到 e 在 table 中的位置了？
只能通过数组下标（索引）操作数组，而数组的下标类型又是 int ，如果 e 是 int 类型，那好说，就直接用 e 来做数组下标（若 e > table.length，则可以 e % table.length 来获取下标），可 key - value 中的 key 类型不一定，所以需要一种统一的方式将 key 转换成 int ，最好是一个 key 对应一个唯一的 int (目前还不可能, int有范围限制，对转换方法要求也极高)，所以引入了 hash 方法
```
static final int hash(Object key) {  
  int h;  
  return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);  // 这里的处理，有兴趣的可以琢磨下；能够减少碰撞  
}
```
实现 key 到 int 的转换。拿到了 key 对应的 int h 之后，最容易想到的对 value 的 put 和 get 操作也许如下 ```java // put
table[h % table.length] = value;

// get
e = table[h % table.length];

直接取模是最容易想到的获取下标的方法，但是最高效的方法吗 ？<br />计算机中的四则运算最终都会转换成二进制的位运算<br />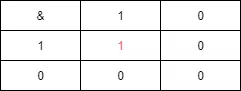![](https://cdn.nlark.com/yuque/0/2022/webp/396745/1642657524852-ecbd3a6b-845c-4d85-80cc-0b35eda446fe.webp#clientId=u9f741eb0-04fb-4&crop=0&crop=0&crop=1&crop=1&from=paste&id=ud447cab3&margin=%5Bobject%20Object%5D&originHeight=91&originWidth=241&originalType=url&ratio=1&rotation=0&showTitle=false&status=done&style=none&taskId=u31cf04b5-f558-44f0-a621-8a59ed8a7ab&title=)<br />可以发现，只有 & 数是1时，& 运算的结果与被 & 数一致
```java
1&1=1;  
0&1=0;  
1&0=0;  
0&0=0;

这同样适用于多位操作数

1010&1111=1010;      => 10&15=10;  
1011&1111=1011;      => 11&15=11;  
01010&10000=00000;   => 10&16=0;  
01011&10000=00000;   => 11&16=0;

是不是又有所发现：10 & 16 与 11 & 16 得到的结果一样，也就是冲突（碰撞）了，那么 10 和 11 对应的 value 会在同一个链表中，而 table 的有些位置则永远不会有元素，这就导致 table 的空间未得到充分利用，同时还降低了 put 和 get 的效率（对比数组和链表）；由于是 2 个数进行 & 运算，所以结果由这两个数决定，如果把这两个数都做下限制，那得到的结果是不是可控制在想要的范围内了？
需要利用好 & 运算的特点，当右边的数的低位二进制是连续的 1 ，且左边是一个均匀的数（需要 hash 方法实现，尽量保证 key 的 h 唯一），那么得到的结果就比较完美了。低位二进制连续的 1，很容易想到 2^n - 1; 而关于左边均匀的数，则通过 hash 方法来实现，这里不做细究了。
自此，2 的 n 次幂的相关问题就清楚了

table 的 length 为什么是 2 的 n 次幂

为了利用位运算 & 求 key 的下标

求索引的时候为什么是：`h&(length-1)`，而不是 `h&length`，更不是 `h%length`

h%length 效率不如位运算快
h&length 会提高碰撞几率，导致 table 的空间得不到更充分的利用、降低 table 的操作效率

问题 5：指定 initialCapacity
当指定了 initialCapacity，HashMap的构造方法有些许不同，如下所示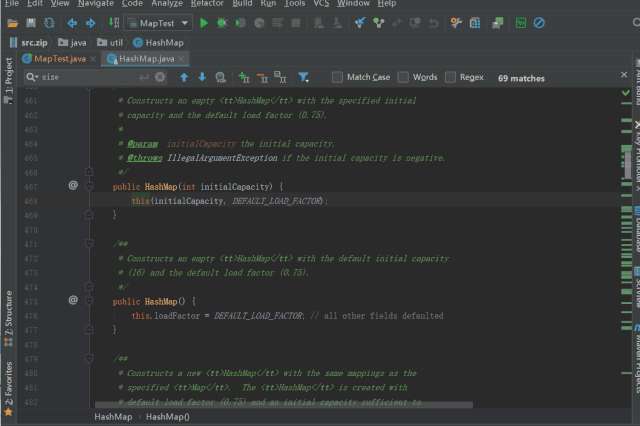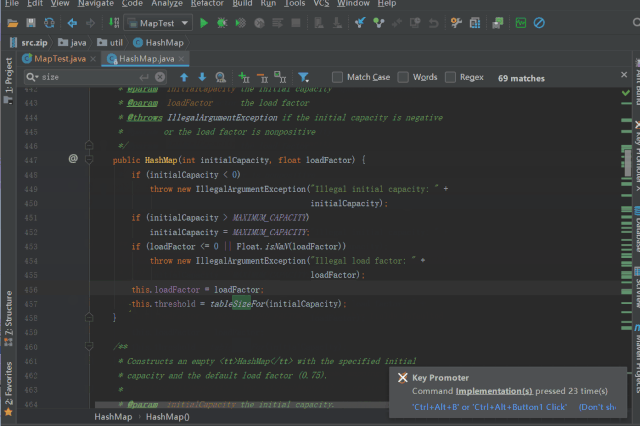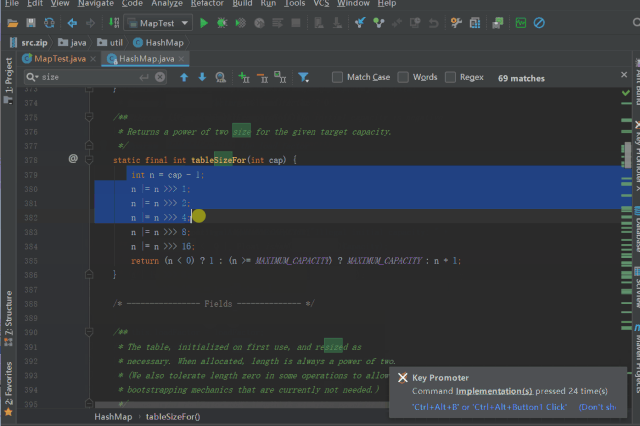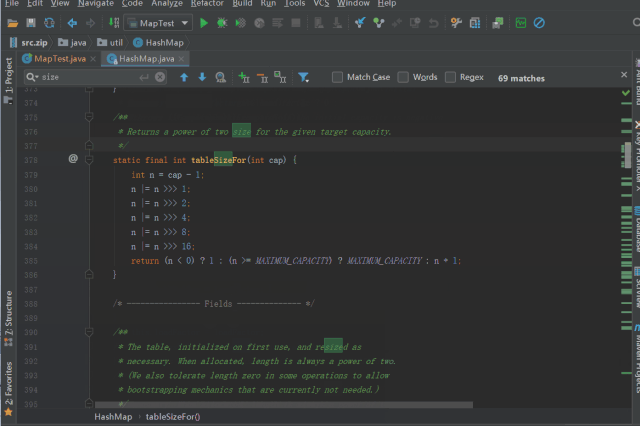

调用 tableSizeFor 进行 threshold 的初始化
```
/**  
* Returns a power of two size for the given target capacity.  
* 返回 >= cap 最小的 2^n  
* cap = 10, 则返回 2^4 = 16;  
* cap = 5, 则返回 2^3 = 8;  
*/  
static final int tableSizeFor(int cap) {  
  int n = cap - 1;  
  n |= n >>> 1;  
  n |= n >>> 2;  
  n |= n >>> 4;  
  n |= n >>> 8;  
  n |= n >>> 16;  
  return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;  
}
```
虽然此处初始化的是 threshold，但后面初始化 table 的时候，会将其用于 table 的 length，同时会重置 threshold 为 table.length * loadFactor
自此，问题 5 也就清楚了

Map map = new HashMap(1000); 当存入多少个元素时会触发map的扩容
此时的 table.length = 2^10 = 1024; threshold = 1024 * 0.75 = 768; 所以存入第 769 个元素时进行扩容

Map map1 = new HashMap(10000); 存入第 10001个元素时会触发 map1 扩容吗
此时的 table.length = 2^14 = 16384; threshold = 16384 * 0.75 = 12288; 所以存入第 10001 个元素时不会进行扩容

问题6：加载因子
为什么加载因子的默认值是 0.75，并且不推荐修改
如果loadFactor太小，那么map中的table需要不断的扩容，扩容是个耗时的过程
如果loadFactor太大，那么map中table放满了也不不会扩容，导致冲突越来越多，解决冲突而起的链表越来越长，效率越来越低
而 0.75 这是一个折中的值，是一个比较理想的值
总结
1、table.length = 2^n，是为了能利用位运算（&）来求 key 的下标，而 h&(length-1) 是为了充分利用 table 的空间，并减少 key 的碰撞
2、加载因子太小， table 需要不断的扩容，影响 put 效率；太大会导致碰撞越来越多，链表越来越长（转红黑树），影响效率；0.75 是一个比较理想的中间值
3、table.length = 2^n、hash 方法获取 key 的 h、加载因子 0.75、数组 + 链表（或红黑树），一环扣一环，保证了 key 在 table 中的均匀分配，充分利用了空间，也保证了操作效率，环环相扣的，而不是心血来潮的随意处理；缺了一环，其他的环就无意义了！
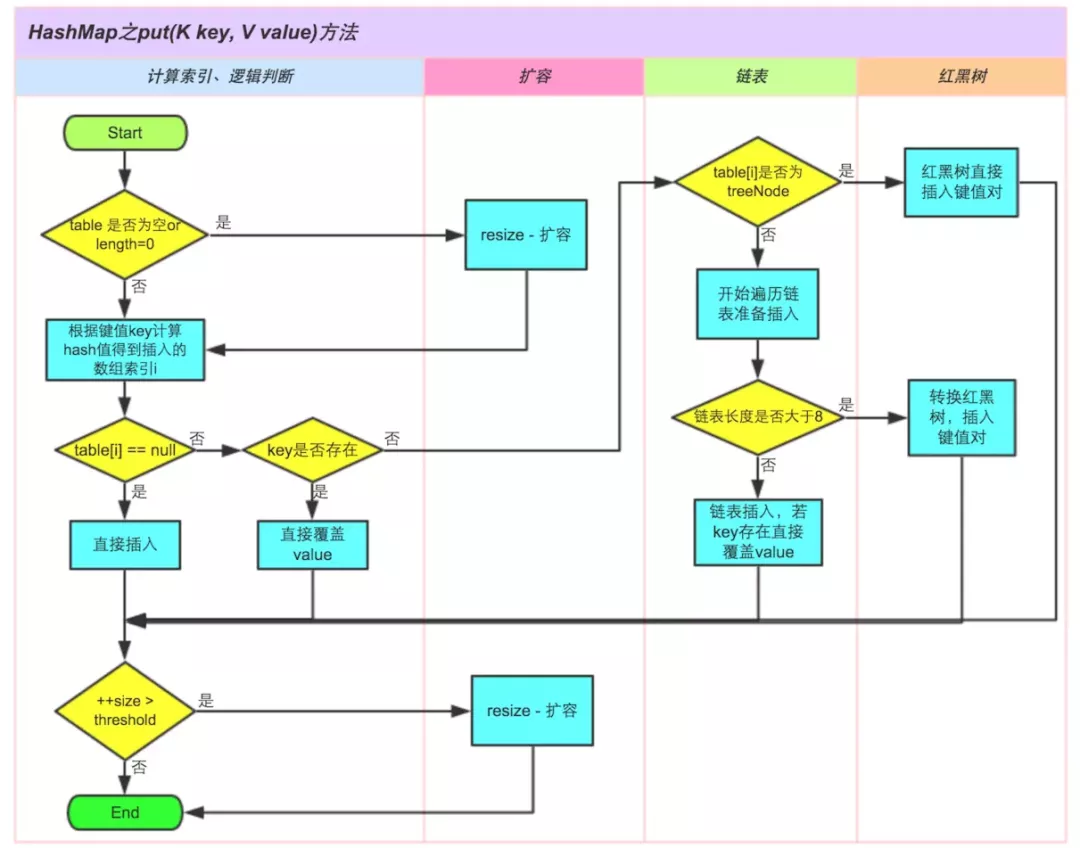
4、put 方法的流程图画

Java 面试题整理

HashMap 面试常见的6连问

问题 1：table 的初始化

table 的初始化时机是什么时候

问题 2 ：table 的扩容

问题 3、4 ：2 的 n 次幂

table 的 length 为什么是 2 的 n 次幂

求索引的时候为什么是：`h&(length-1)`，而不是 `h&length`，更不是 `h%length`

问题 5：指定 `initialCapacity`

`Map map = new HashMap(1000);` 当存入多少个元素时会触发map的扩容

`Map map1 = new HashMap(10000);` 存入第 10001个元素时会触发 map1 扩容吗

问题6：加载因子

总结

HashMap 面试常见的6连问

问题 1：table 的初始化

table 的初始化时机是什么时候

问题 2 ：table 的扩容

问题 3、4 ：2 的 n 次幂

table 的 length 为什么是 2 的 n 次幂

求索引的时候为什么是：h&(length-1)，而不是 h&length，更不是 h%length

问题 5：指定 initialCapacity

Map map = new HashMap(1000); 当存入多少个元素时会触发map的扩容

Map map1 = new HashMap(10000); 存入第 10001个元素时会触发 map1 扩容吗

问题6：加载因子

总 结

求索引的时候为什么是：`h&(length-1)`，而不是 `h&length`，更不是 `h%length`

问题 5：指定 `initialCapacity`

`Map map = new HashMap(1000);` 当存入多少个元素时会触发map的扩容

`Map map1 = new HashMap(10000);` 存入第 10001个元素时会触发 map1 扩容吗

总结