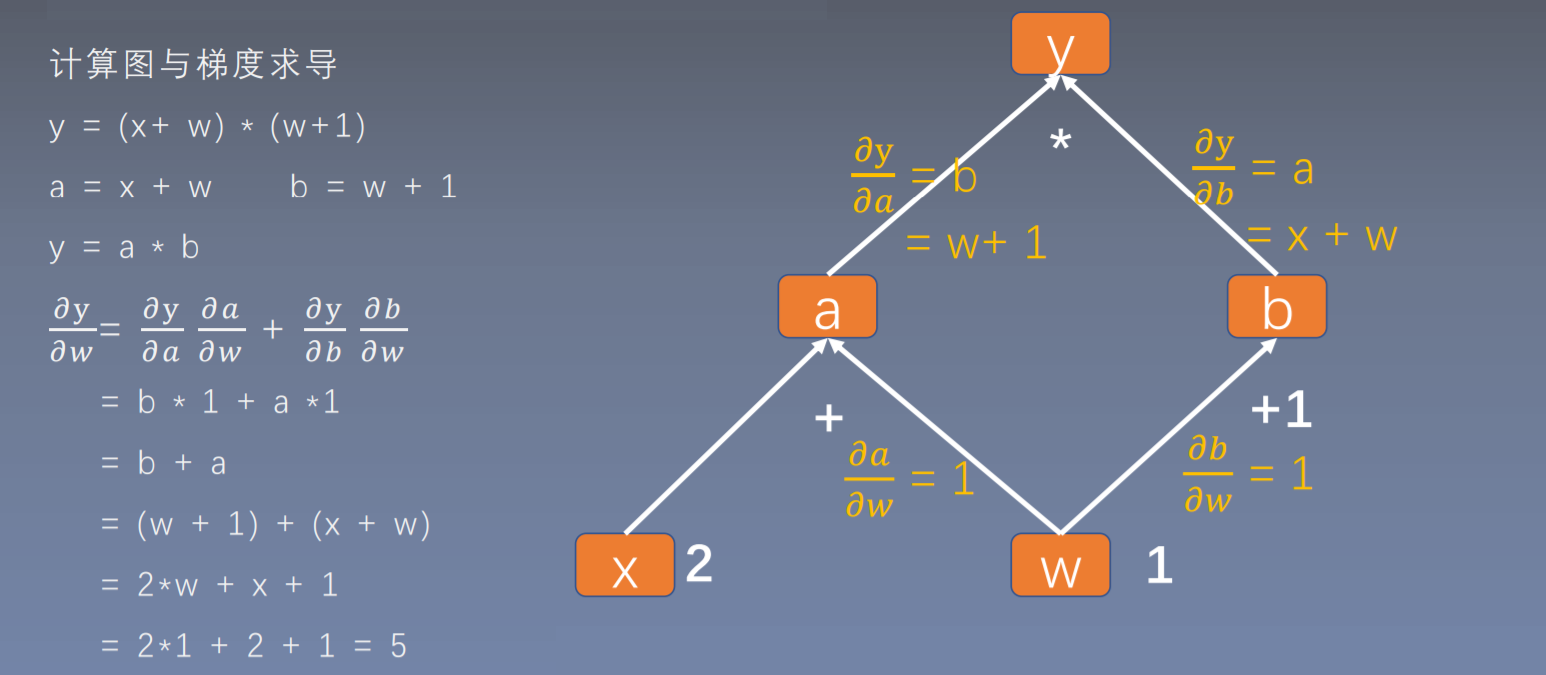
- 计算图
- PyTorch的动态图机制
一、计算图
1.1 计算图的表示
- 计算图是用来描述运算的有向无环图
- 计算图有两个主要元素:结点(Node)和 边(Edge)
- 结点表示数据,如向量,矩阵,张量
- 边表示运算,如加、减、乘、除、卷积等
- 用计算图表示:
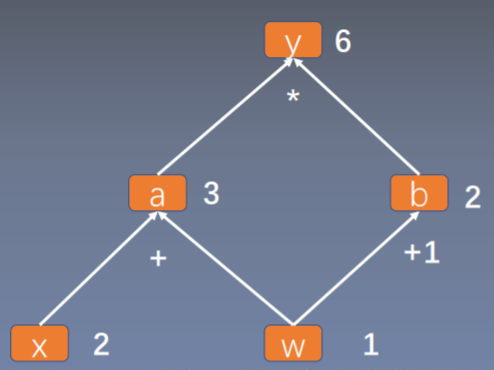
- 叶子结点:用户创建的结点称为叶子结点,如
X
与
W
- 叶子节点是整个计算图的根基,例如前面求导的计算图,在前向传导中的a、b和y都要依据创建的叶子节点x和w进行计算的。同样,在反向传播过程中,所有梯度的计算都要依赖叶子节点。
- 设置叶子节点主要是为了节省内存,在梯度反向传播结束之后,非叶子节点的梯度都会被释放掉。可以根据代码分析一下非叶子节点a、b和y的梯度情况。
is_leaf: 指示张量是否为叶子结点- 所有的梯度计算都需要叶子节点
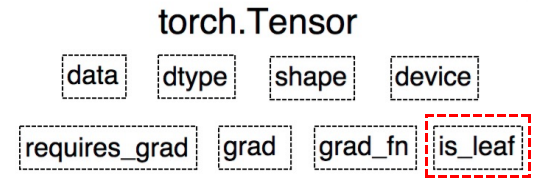
grad_fn: 记录创建该张量时所用的方法(函数)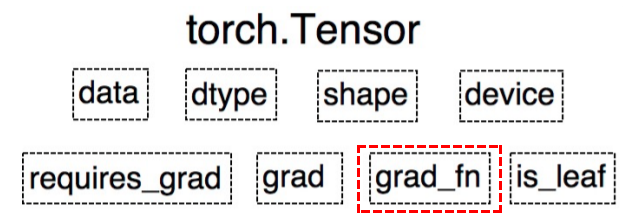
```python import torchy.grad_fn = <MulBackward0>a.grad_fn = <AddBackward0>b.grad_fn = <AddBackward0>
w = torch.tensor(1, dtype=float, requires_grad=True) x = torch.tensor(2, dtype=float, requires_grad=True)
a = torch.add(w, x) a.retain_grad() # 在反向传播之后,仍然保留非叶子节点的梯度 b = torch.add(w, 1) y = torch.mul(a, b)
y.backward() print(w.grad)
查看叶子结点
print(“is_leaf:\n”, w.is_leaf, x.is_leaf, a.is_leaf, b.is_leaf, y.is_leaf)
查看梯度
print(“gradient:\n”, w.grad, x.grad, a.grad, b.grad, y.grad) # 反向传播之后,会将非叶子节点释放掉,节省内存开销
查看 grad_fn
print(“grad_fn:\n”, w.grad_fn, x.grad_fn, a.grad_fn, b.grad_fn, y.grad_fn) # 记录创建该张量时所用的方法

<a name="pRQA6"></a>
# 二、动态图机制
<br />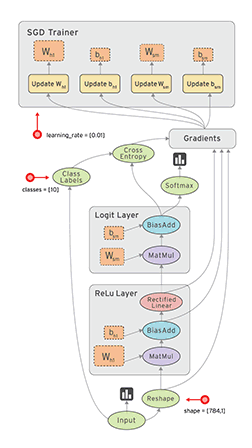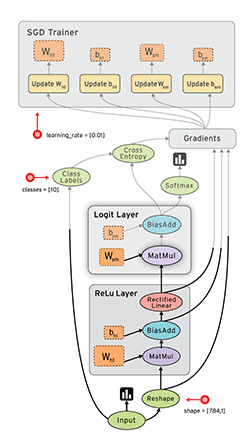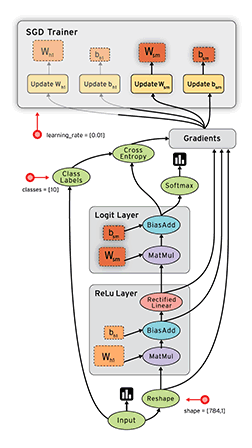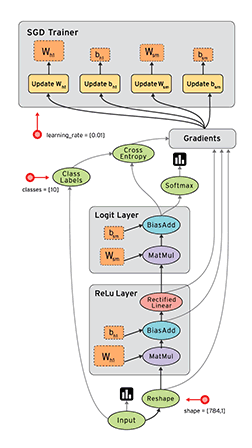<br />**TensorFlow静态图演示**
> 在上面这个图中,框代表的就是节点,带箭头的线代表边。tensorflow使用的是静态图,是先将图搭建好之后,再input数据进去。
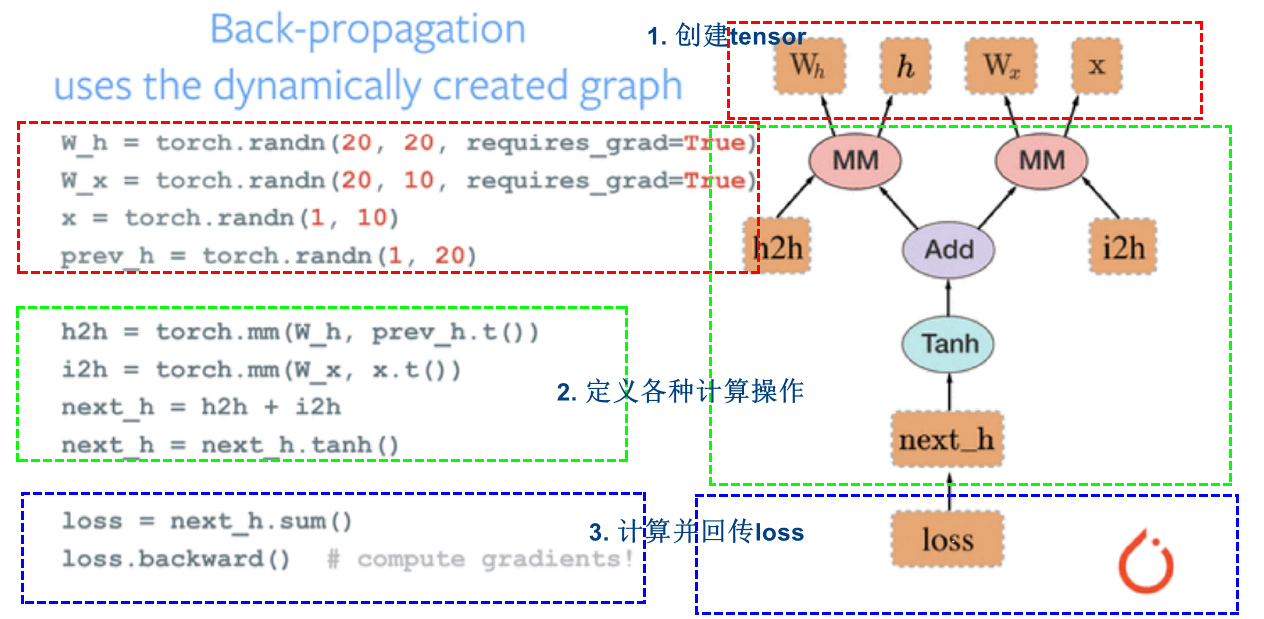<br />**PyTorch动态图**
> 动态图的搭建是根据每一步的计算搭建的,而tensorflow是先搭建所有的计算图之后,再把数据输入进去。这就是动态图和静态图的区别。
```python
# 1. 创建四个tensot
W_h = torch.randn(20, 20, requires_grad=True)
W_x = torch.randn(20, 10, requires_grad=True)
x = torch.randn(1, 10)
prev_h = torch.randn(1, 20)
# 2. 定义各种数据操作
h2h = torch.mm(W_h, prev_h.t()) # 将W_h和prev_h进行相乘,得到一个新张量h2h
i2h = torch.mm(W_x, x.t()) # 将W_x和x进行相乘,等到一个新张量i2h
next_h = h2h + i2h # 创建加法操作
next_h = next_h.tanh() # 使用激活函数
# 3. 计算并回传loss
loss = next_h.sum() #计算损失函数
loss.backward() #梯度反向传播