torch.autograd- 逻辑回归
一、 torch.autograd ——自动求导系统
深度学习模型的训练就是不断更新权值,权值的更新需要求解梯度,梯度在模型训练中是至关重要的。然而求解梯度十分繁琐,pytorch提供自动求导系统。我们不需要手动计算梯度,只需要搭建好前向传播的计算图,然后根据pytorch中的 autograd方法 就可以得到所有张量的梯度。
01. torch.autograd.backward()

- 功能:自动求取梯度
tensor:用于求导的张量,如lossretain_graph:保存计算图;由于pytorch采用动态图机制,在每一次反向传播结束之后,计算图都会释放掉。如果想继续使用计算图,就需要设置参数retain_graph为True;create_graph:创建导数计算图,用于高阶求导,例如二阶导数、三阶导数等等;grad_tensors:多梯度权重;当有多个loss需要去计算梯度的时候,就要设计各个loss之间的权重比例。
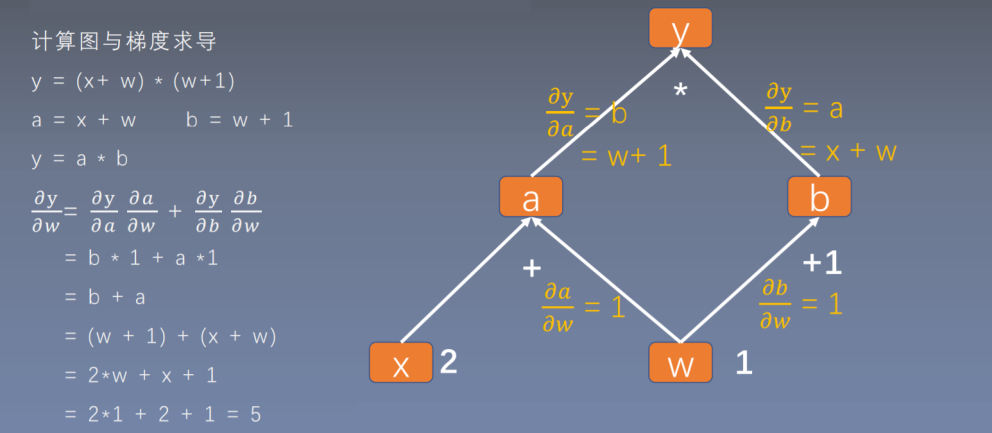
w = torch.tensor([1.], requires_grad=True)x = torch.tensor([2.], requires_grad=True)a = torch.add(w, x)b = torch.add(w, 1)y = torch.mul(a, b)y.backward(retain_graph=True)# print(w.grad)y.backward()
从代码中可以发现对y求导使用的是 y.backward() 方法,也就是张量中的类方法。我们上面介绍的是 torch.autograd.backward() 。这两个方法之间有什么联系呢?
通过pycharm中的断点调试,可以发现 y.backward() 是 tensor.py 中的一个类方法的函数。这个函数只有一行代码,就是调用 torch.autograd.backward() 。
def backward(self, gradient=None, retain_graph=None, create_graph=False):torch.autograd.backward(self, gradient, retain_graph, create_graph)
从代码调试中可以知道张量中的 backward() 方法实际直接调用了 torch.autograd.backward() 。
1.1 retain_grad
backward() 中有一个 retain_grad 参数,它是用来保存计算图的,如果还想执行一次反向传播 ,必须将 retain_grad 参数设置为 retain_grad=True ,否则代码会报错。因为如果没有 retain_grad=True ,每进行一次backward之后,计算图都会被清空,没法再进行一次backward()操作。
1.2 gradient
backward() 中还有一个比较重要的参数 gradient ,用于设置多个梯度之间的权重,具体的使用可以参考一下下面的代码:
w = torch.tensor([1.], requires_grad=True)x = torch.tensor([2.], requires_grad=True)a = torch.add(w, x) # retain_grad()b = torch.add(w, 1)y0 = torch.mul(a, b) # y0 = (x+w) * (w+1)y1 = torch.add(a, b) # y1 = (x+w) + (w+1) dy1/dw = 2loss = torch.cat([y0, y1], dim=0) # [y0, y1], 损失函数由两部分组成grad_tensors = torch.tensor([1.,2.]) # 设置两部分损失函数的权重loss.backward(gradient=grad_tensors) # gradient 传入 torch.autograd.backward()中的grad_tensorsprint(w.grad) # w = 1*5 + 2*2 = 9,输出为9
02. torch.autograd.grad

- 功能:求取梯度
outputs:用于求导的张量,如lossinputs:需要梯度的张量,如上面代码中的wcreate_graph:创建导数计算图,用于高阶求导retain_graph:保存计算图grad_outputs:多梯度权重 ```python x = torch.tensor([3.], requires_grad=True) y = torch.pow(x, 2) # y = x**2
grad_1 = torch.autograd.grad(y, x, create_graph=True) # grad_1 = dy/dx = 2x = 2 * 3 = 6 print(grad_1)
grad_2 = torch.autograd.grad(grad_1[0], x) # grad_2 = d(dy/dx)/dx = d(2x)/dx = 2 print(grad_2)
- autograd小贴士- 梯度不自动清零;如果不手动清零,会将梯度叠加- 依赖于叶子结点的结点, `requires_grad` 默认为 `True`- 叶子结点不可执行in-place(原位操作)。 `_` :下划线表示原位操作```python# ============ 梯度不自动清零代码演示 ============ #w = torch.tensor([1.], requires_grad=True)x = torch.tensor([2.], requires_grad=True)for i in range(4):a = torch.add(w, x)b = torch.add(w, 1)y = torch.mul(a, b)y.backward()print(w.grad)# tensor([5.])# tensor([10.])# tensor([15.])# tensor([20.])w.grad.zero_()print(w.grad)# tensor([5.])# tensor([5.])# tensor([5.])# tensor([5.])
从代码的输出结果看, w.grad 的值不断累加。梯度不会自动清零。为了能够实现梯度清零,需要在代码中加上一段代码 w.grad.zero_() 进行梯度自动清零处理。
# ============ 依赖于叶子结点的结点 ============ #
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)
print(a.requires_grad, b.requires_grad, y.requires_grad)
# 输出:True True True
通过代码可以看到,其中的 w 和 x 是叶子节点,依赖于叶子节点的点分别为a和b,通过检查其 requires_grad 可以知道为 True ,因为其依赖于叶子节点,所以 requires_grad 默认为 True ;
a = torch.ones((1, ))
print(id(a), a)
a = a + torch.ones((1, )) # `+` 不是原地操作
print(id(a), a)
a += torch.ones((1, )) # `+=` 是原地操作
print(id(a), a)
# 结果:
# 2407907922136 tensor([1.])
# 2407959919640 tensor([2.])
# 2407959919640 tensor([3.])
- 在pytorch中经常加后缀
_来表示原地in-place operation,比如说.add() 或者.scatter()。我们可以将in_place操作简单的理解类似于python中的”+=”,”-=”等操作。 in-place:原位操作:在不改变数据内存地址的前提下,对数据的值进行修改。在原始内存中改变数据- 如果将一个叶子结点进行in-place操作,其结果如下代码所示,会报错:
```python
============ 叶子结点不可执行in-place (原位操作) ============
w = torch.tensor([1.], requires_grad=True) x = torch.tensor([2.], requires_grad=True)
a = torch.add(w, x) b = torch.add(w, 1) y = torch.mul(a, b)
w.add_(1) y.backward()
报错:
RuntimeError: a leaf Variable that requires grad has been used in an in-place operation.
- 为什么叶子结点不能执行in-place操作呢?可以通过计算图的梯度求解过程看一下:
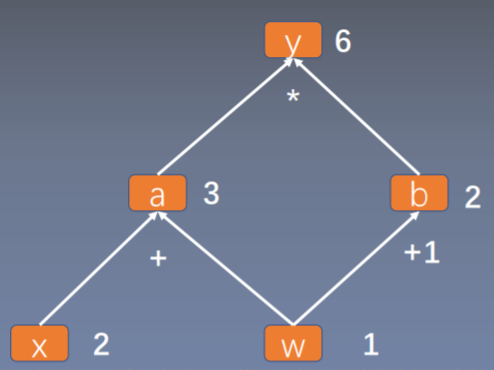<br />通过上图可以发现,如果要求解w的梯度,需要用到,而,也就是在反向传播的时候是需要用到 `叶子张量w` 的。而在前向传播的时候, `y` 会记录w的地址,到反向传播的时候,在用到的时候根据地址去寻找 `w` 的数据。如果在反向传播之前改变了 `w` 的地址当中的数据,梯度求解就会出错,这就是叶子结点不能执行in-place操作的原因。
<a name="LK7BD"></a>
# 二、逻辑回归
逻辑回归是**线性的二分类模型**;模型表达式:<br />称为 `Sigmoid函数` ,也称为 `Logistic函数` 。<br />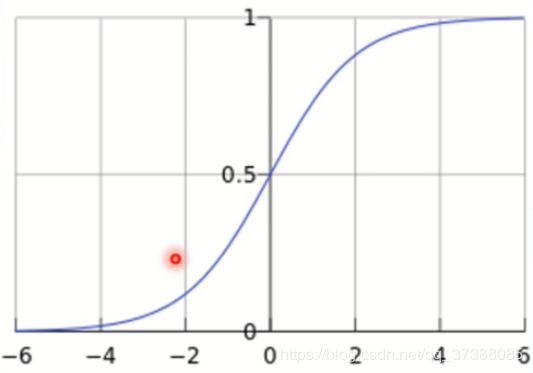
逻辑回归是二分类模型,根据y值对数据进行分类;分类依据如下:<br />逻辑回归是线性的,首先看一下线性回归模型与逻辑回归模型之间的区别;<br />
- 线性回归是分析自变量X与因变量y(标量)之间关系的方法
- 逻辑回归是分析自变量X与因变量y(概率)之间关系的方法
线性回归模型中自变量为X,因变量为y,两者之间的关系为
逻辑回归是在线性回归的基础上加了一个激活函数 `sigmoid()` ,从sigmoid函数的曲线图可以看出,如果没有激活函数 `sigmoid` ,逻辑回归模型还是可以进行二分类的。可以将分类为类别1,当时判别为类别0。等价于,等价于。所以在逻辑回归中只需也可以用来做二分类。**只是为了更好地描述分类置信度**,所以采用sigmoid函数将输出映射到0-1,符合一个概率取值。
逻辑回归还有一个别名是**对数几率回归**,几率是概率取值,它表示的是样本x为正样本的可能性,对几率取一个对数就得到对数几率。这个公式是和逻辑回归公式是等价的。对数几率回归公式:<br />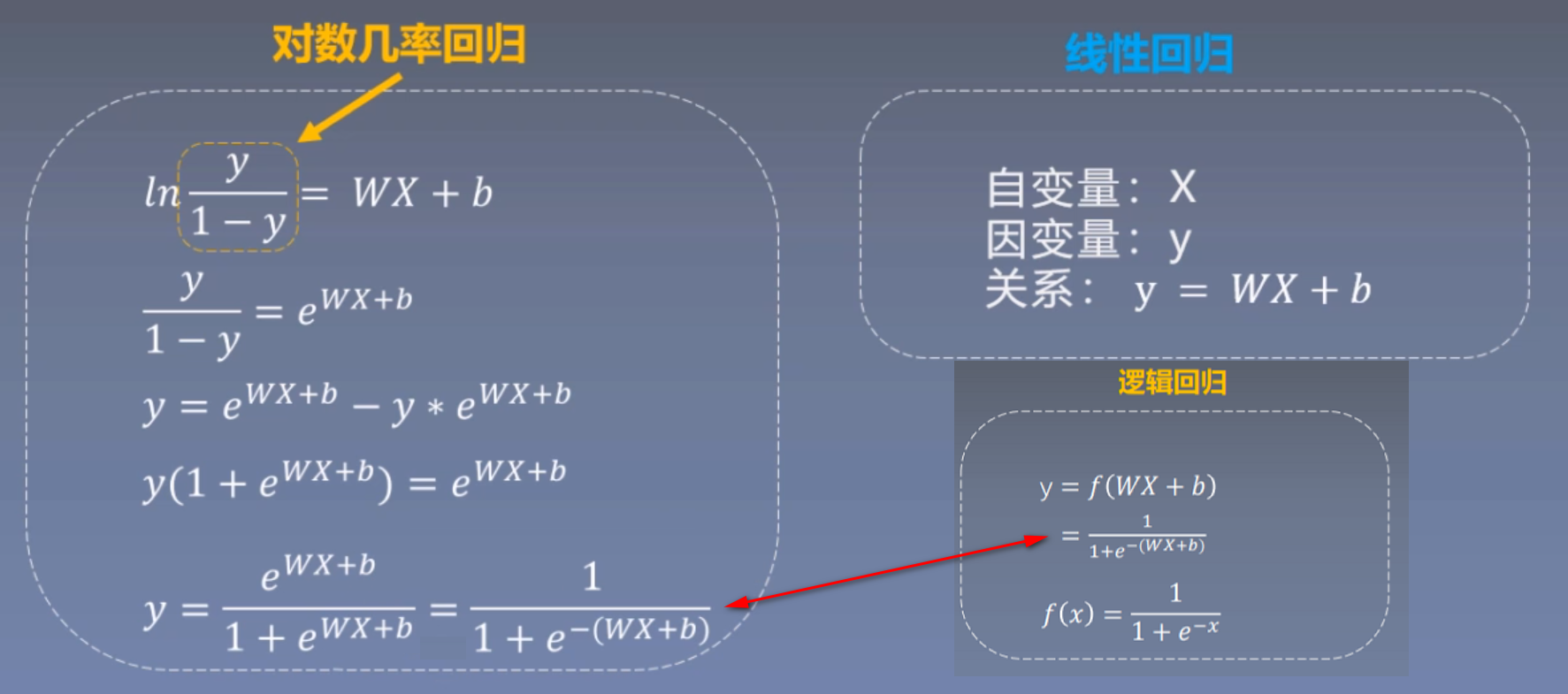<br />线性回归模型是用去拟合,而对数几率回归是用去拟合一个对数几率 ;
还有一种公式为对数回归,对数回归的公式表示为:
<a name="3HLlU"></a>
## 逻辑回归模型的训练过程
在介绍代码之前,先简单介绍一下机器学习训练步骤:<br />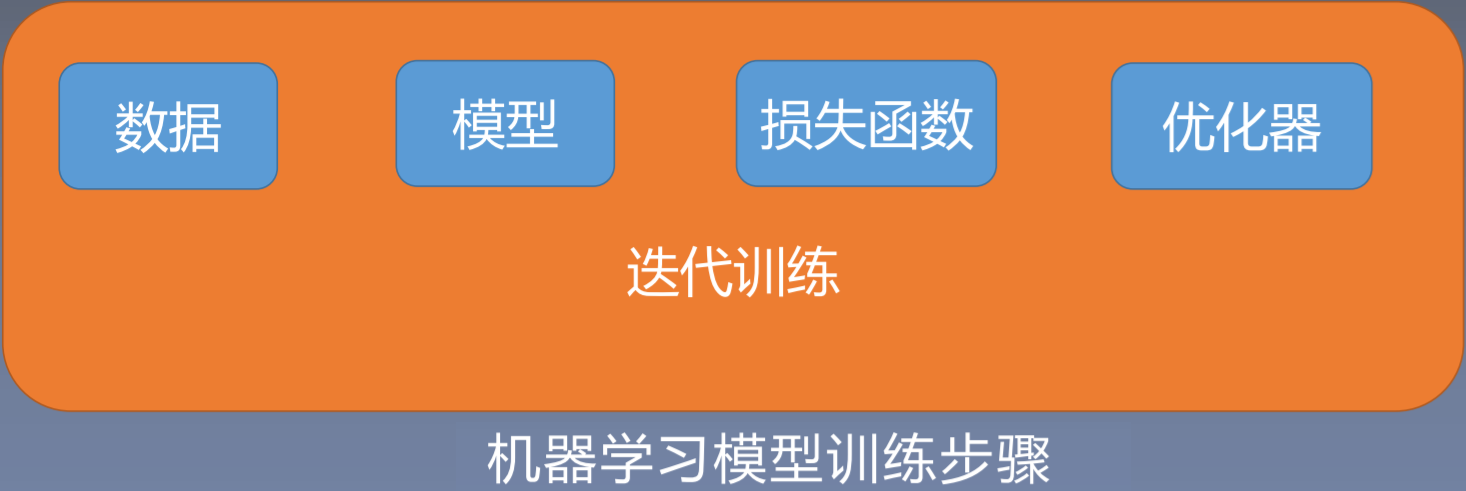
1. 一个机器学习模型的训练首先要获取数据,也称之为**数据模块**,在数据模块中,可能涉及数据的采集、数据的清洗、数据划分和预处理。经过对数据的一系列处理,使得数据可以直接输入到模型。
1. 第二个模块是**模型模块**,可以根据任务的难易程度选择简单的线性模型或者复杂的神经网络模型。
1. 第三个模块是**损失函数的选择**,可以根据不同的任务选择不同的损失函数,比如在线性回归模型中采用均方差损失函数;如果是分类任务,可以用交叉熵。有了损失函数,就可以求取梯度。
1. 得到梯度之后,可以选择某一种优化方式,也就是**优化器**。采用某一种优化器更新我们的权值,这就是优化器模块的功能。
有了**数据、模型、损失函数、优化器**,才可以进行反复的迭代训练。这就是迭代训练模块。现在通过代码看一下怎么通过这五个模块建立逻辑回归模型。
```python
# -*- coding: utf-8 -*-
# @Time : 2020/5/1 18:56
# @Author : DarrenZhang
# @FileName: logsitic_regression.py
# @Software: PyCharm
# @Blog :https://www.yuque.com/darrenzhang
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
torch.manual_seed(10)
# ============================ step 1/5 生成数据 ============================
sample_nums = 100
mean_value = 1.7
bias = 1
n_data = torch.ones(sample_nums, 2)
x0 = torch.normal(mean_value * n_data, 1) + bias # 类别0 数据 shape=(100, 2)
y0 = torch.zeros(sample_nums) # 类别0 标签 shape=(100, 1)
x1 = torch.normal(-mean_value * n_data, 1) + bias # 类别1 数据 shape=(100, 2)
y1 = torch.ones(sample_nums) # 类别1 标签 shape=(100, 1)
train_x = torch.cat((x0, x1), 0)
train_y = torch.cat((y0, y1), 0)
# ============================ step 2/5 选择模型 ============================
class LR(nn.Module):
def __init__(self):
super(LR, self).__init__()
self.features = nn.Linear(2, 1)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
x = self.features(x)
x = self.sigmoid(x)
return x
lr_net = LR() # 实例化逻辑回归模型
# ============================ step 3/5 选择损失函数 ============================
loss_fn = nn.BCELoss()
# ============================ step 4/5 选择优化器 ============================
lr = 0.01 # 学习率
optimizer = torch.optim.SGD(lr_net.parameters(), lr=lr, momentum=0.9)
# ============================ step 5/5 模型训练 ============================
for iteration in range(1000):
# 前向传播,将训练数据输入模型,得到模型的输出
y_pred = lr_net(train_x)
# 计算 loss,有了模型的输出就可以计算loss
loss = loss_fn(y_pred.squeeze(), train_y)
# 反向传播,有了loss,进行反向传播梯度求导
loss.backward()
# 更新参数,有了梯度就可以更新权值等一系列参数
optimizer.step()
# 清空梯度
optimizer.zero_grad()
# 绘图
if iteration % 20 == 0:
mask = y_pred.ge(0.5).float().squeeze() # 以0.5为阈值进行分类
correct = (mask == train_y).sum() # 计算正确预测的样本个数
acc = correct.item() / train_y.size(0) # 计算分类准确率
plt.scatter(x0.data.numpy()[:, 0], x0.data.numpy()[:, 1], c='r', label='class 0')
plt.scatter(x1.data.numpy()[:, 0], x1.data.numpy()[:, 1], c='b', label='class 1')
w0, w1 = lr_net.features.weight[0]
w0, w1 = float(w0.item()), float(w1.item())
plot_b = float(lr_net.features.bias[0].item())
plot_x = np.arange(-6, 6, 0.1)
plot_y = (-w0 * plot_x - plot_b) / w1
plt.xlim(-5, 7)
plt.ylim(-7, 7)
plt.plot(plot_x, plot_y)
plt.text(-5, 5, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color': 'red'})
plt.title("Iteration: {}\nw0:{:.2f} w1:{:.2f} b: {:.2f} accuracy:{:.2%}".format(iteration, w0, w1, plot_b, acc))
plt.legend()
plt.show()
plt.pause(0.5)
if acc > 0.99:
break

