1. 梯度消失与爆炸
  2. Xavier方法
  3. Kaiming方法
  4. 常用初始化方法

一、梯度消失与爆炸

二、Xavier方法

方差一致性：保持数据尺度维持在恰当范围，通常方差为1
适合激活函数：饱和函数，如Sigmoid，Tanh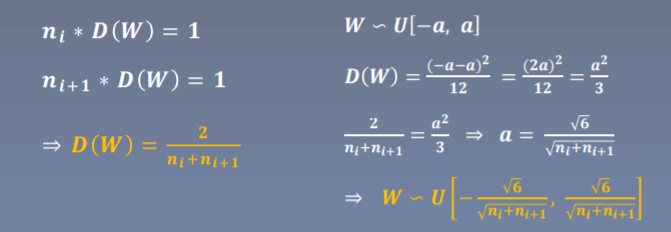
image.png

参考文献：Understanding the difficulty of training deep feedforward neural networks

三、Kaiming方法

方差一致性：保持数据尺度维持在恰当范围，通常方差为1
激活函数：ReLU及其变种

  1. nn.init.kaiming_normal_(m.weight.data)

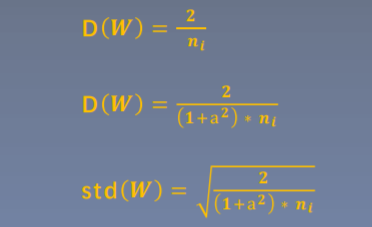
image.png

参考文献：Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification

十种初始化方法

  1. Xavier均匀分布
  2. Xavier正态分布
  3. Kaiming均匀分布
  4. Kaiming正态分布
  5. 均匀分布
  6. 正态分布
  7. 常数分布
  8. 正交矩阵初始化
  9. 单位矩阵初始化
  10. 稀疏矩阵初始化
    1. nn.init.calculate_gain(nonlinearity, param=None)
    nn.init.calculate_gain()
  • 主要功能：计算激活函数的方差变化尺度
  • 主要参数