[译文]Are Deep Neural Networks Dramatically Overfitted?

博客针对DNN的泛化性提出了疑问：DNN模型参数量巨大，但没有过拟合，这与经典机器学习理论相违背。
博客首先阐述了经典的模型选择方法- simple is best。
其次，描述了DNN模型的表达能力-万能近似定理，以及拟合随机样本。
最后，表述了经典的bias-variance 风险曲线（复合奥姆剃须刀原理）无法解释 DNN的拟合现象，并给出了双U风险曲线、本质维度、彩票理论才解释DNN的拟合问题。

整体结论是：DNN模型虽然很大，但是实际work的参数并不多，参数量不能反映模型复杂度。寄予希望新的理论能解释。

原文链接：Are Deep Neural Networks Dramatically Overfitted?
如果你有深度学习和 传统机器学习的两方面的使用经验，你可能会产生疑问：深度神经网络有非常多的参数并且训练误差非常小，一般来说，这样的模型应该存在过拟合问题，DNN模型是如何推广到样本外的数据？
本文将会讨论一些关于深度学习模型复杂度度量和泛化性的论文，希望能理解清楚 为什么DNN可以泛化？

1、关于压缩、模型选择的经典理论

假设我们现在在某个数据集上有一个分类问题，可以采用很多模型去解决该问题，从简单的线性模型 到 使用硬盘空间记忆整个数据集（暴力记忆）。那么到底哪个模型更好呢？如果仅仅关心训练集上的准确率，肯定是 记忆性的方法最好。好吧，这听起来是个糟糕的想法！！<br />   其实，存在很多经典的理论方法 指导我们在不同的场景不同时间用何种类型的模型。

1.1 奥卡姆剃刀原理

Occam’s Razor是 William of Ockham 在14世纪提出用于解决问题的通俗性原则。

Simpler solutions are more likely to be correct than complex ones.

当我们 多个可解释问题的候选理论，且必须从中选出一个作为最佳，如何做出选择？上述原则会是一个强有力的指导原则。对于一个问题来说，过多的非必要假设看起来很有道理，但是将会难以推广到其他类似的问题上 或者说难以总结出更普遍的基础性原则。
比如说，数百年前人们指出由于Rayleigh scattering 天空在白天时是蓝色的、在傍晚是是微红的。这是两个不同时刻的现象，看起来是不同的，人们曾经针对这两个现象分别提出了不同的解释，最后统计的、简单的版本获得认可。

1.2 最小描述长度原理

Occam's Razor原则，可以类似地应用在机器学习模型上。正式概念称为：Minimum Description Length （MDL）principle，该原则用于：给定数据集情况下，不同的模型、解释的对比。

Comprehension is compression.

MDL原则的本质观点是：把学习问题看成数据压缩问题。通过压缩数据，我们可以从数据中总结出规律、抽象出模式，并且能够把规律、模式推广（泛化）到未知数据。Information bottleneck （信息瓶颈理论）认为 首先 使用最小化泛化误差训练DNN模型并用于数据表征；其次，通过噪声去除的方法 来 压缩表征。
MDL原则把模型看成是压缩的一部分，因此这会限制模型的大小。

表示模型的长度描述，单位bits；表示 数据D使用模型H编码时的长度描述。
简单来说，最好的模型是 能够包含编码数据和模型本身的最小模型。从这个原则来看，前面提到的记忆法显然不是很好的选择。

1.3 Kolmogorov Complexity

…..

2、深度模型的表达力

 与传统机器学习模型相比，深度神经网络模型有超大量的参数。如果我们使用MDL原则 来评估DNN模型的复杂度，把参数数量看成模型长度描述，DNN模型看起来是很糟糕的。<br />     但是，海量的参数是DNN模型强表达力的必要前提。因为DNN模型的超大模型容量，能够捕获到任何复杂数据表征，因此DNN模型在实际应用中取得了极大的成功。

2.1 万能近似定理

 Universal Approximation Theorem描述如下：**前馈神经网络，只需具备单层隐含层和有限个神经单元，就能以任意精度拟合任意复杂度的函数**。尽快单层的前馈神经网络足以表示任何函数，但是网络的宽度将会指数增长。Universal Approximation Theorem 不能保证模型的泛化性能。通常，增加网络层（网络深度）能够减少神经元的个数。<br />     总而言之，依据UAT理论，我们总是可以找到一个满足误差需求的DNN网络来拟合目标函数，代价是：模型可能非常大。

2.2 有限样本下两层NN网络的表达力

UAT理论没有讨论有限样本的情况，文献[5]证明了有限样本下，双层NN网络的表达能力。

T**here exists a two-layer neural network with ReLU activations and 2n+d weights that can represent any function on a sample of size n in d dimen**sions.

2.3 DNN模型可以学习随机噪声

从上节我们可以知道两层的神经网络可以看做是万能的近似器，因此能够学习到没有任何规律的随机噪声。即使图片分类的标签是随机打乱的，由于DNN模型的强表达力，依然能够保证训练误差为0，并且有无正则项都一样。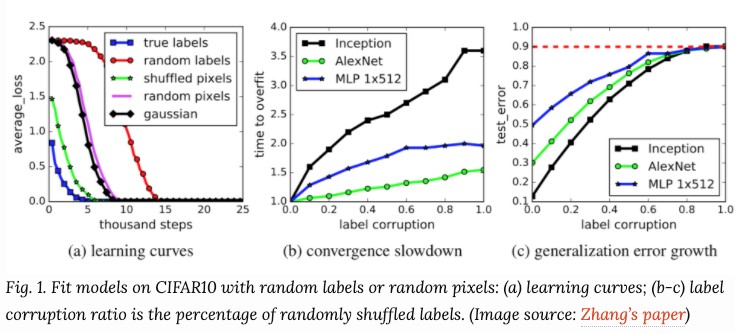

3. 深度学习模型是不是过拟合了？

 over-parameterized的深度学习模型经常在训练集上得到完美的结果。从传统观点来看，比如：bias-variance trade-offs理论，这样的模型将难以泛化到未知的测试数据集上。 但实际上，所谓的过拟合的深度学习模型在测试集上也有很有的表现。哈哈哈....有趣，为啥呢？

3.1 Modern Risk Curve for Deep Learning

传统的机器学习模型使用U型的风险曲线来评估 bias-variance trade off ，定量地分析模型的泛化性。
随着模型的增大（参数变多），训练误差变小，但是一旦模型复杂度越过了欠拟合-过拟合的分界点，测试误差（泛化误差）会开始变大，这和奥姆剃须刀原理不谋而合。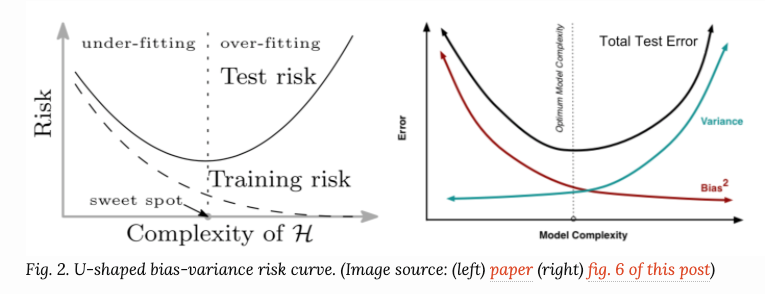

非常不幸地是，上述观点不能应用到深度学习模型上。文献[7] 提出双U型风险曲线。一旦参数足够大，经验风险将进入另一个曲线。论文提出了两个理由：a、参数的数量无法良好的评估bias。b. 参数的模值变小，可以看成模型更简单了。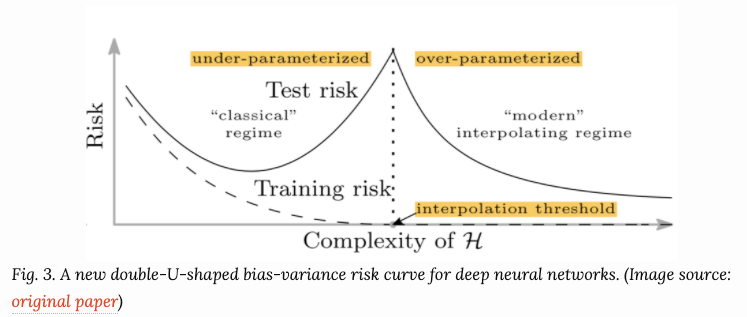

3.2 正则化不是泛化的关键

正则化常用于控制过拟合，提高模型的泛化能力。在文献[5]的实验中表明，显示的泛化手段（数据增强、权重衰减、dropout等）都无法显著提高模型的泛化能力。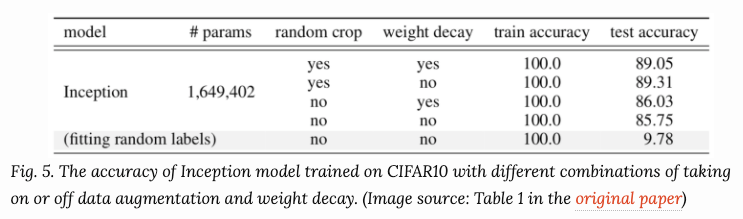

3.3 Intrinsic Dimension-本质维度

在深度学习领域，参数数量和模型过拟合不存在关联性，可以认为参数数量的多少不能代表DNN模型的真实复杂度。
最近的研究，文献[9]提出Intrinsic Dimension。即：参数数量不代表复杂度。

3.4 Heterogeneous Layer Robustness - 不同层的鲁棒性

文献[8]探索了网络中不同层的作用。
结论如下：网络能够自我约束降低模型复杂度

Over-capacitated deep networks trained with stochastic gradient have low-complexity due to self-restricting the number of critical layers

re-initialization可以作为一种减少参数数量的方法，这和本质维度的理念是一样。

3.5 The Lottery Ticket Hypothesis - 彩票假设

文献[9] 提到，虽然网络很大，但实际上只有一个子网络参数对模型效果有影响，因此模型没有过拟合。

参考文献
[1]Understanding the Bias-Variance Tradeoff
[3]Peter Grunwald. “A Tutorial Introduction to the Minimum Description Length Principle”. 2004.
[5]Zhang, Chiyuan, et al. “Understanding deep learning requires rethinking generalization.” ICLR 2017.
[7]Mikhail Belkin, et al. “Reconciling modern machine learning and the bias-variance trade-off.” arXiv:1812.11118, 2018.
[8] Chiyuan Zhang, et al. “Are All Layers Created Equal?” arXiv:1902.01996, 2019.
[9]Chunyuan Li, et al. “Measuring the intrinsic dimension of objective landscapes.” ICLR 2018.
[10] Jonathan Frankle and Michael Carbin. “The lottery ticket hypothesis: Finding sparse, trainable neural networks.” ICLR 2019.