原文: https://pythonspot.com/binary-numbers-and-logical-operators/

我们之前已经看过简单的数字和运算。 在本文中,您将学习数字在计算机内部的工作方式以及与此相关的一些魔术 :-)
更详细:虽然这在 Web 应用程序或大多数桌面应用程序中没有直接用处,但了解它非常有用。
在本文中,您将学习如何在 Python 中使用二进制数,如何将其转换为小数以及如何对它们进行按位运算。
二进制数
在最低层次上,计算机没有任何数字概念,除了“有信号”或“无信号”。您可以将其视为电灯开关:开关打开或关闭。
这些微小的信息,是您可以在计算机中存储的最小信息,称为位。我们将位表示为低(0)或高(1)。
为了表示大于 1 的数字,使用一系列位的主意诞生了。 一个八位的序列可以存储更大的数字,这称为字节。 由一和零组成的序列称为二进制。我们传统的十位数计数系统称为十进制。
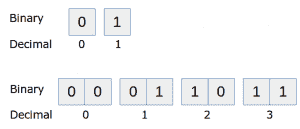
二进制数及其十进制表示形式。
让我们在实践中看看:
# Prints out a few binary numbers.print int('00', 2)print int('01', 2)print int('10', 2)print int('11', 2)
第二个参数 2 告诉 Python 我们有一个基于 2 个元素(1 和 0)的数字。 要将字节(8 位)转换为十进制,只需在第一个参数中写入 8 位的组合即可。
# Prints out a few binary numbers.print int('00000010', 2) # outputs 2print int('00000011', 2) # outputs 3print int('00010001', 2) # outputs 17print int('11111111', 2) # outputs 255
电脑如何做到这一点? 每个数字(从右到左)乘以 2 的幂。
数字00010001是(1 x 2^0) + (0 x 2^1) + (0 x 2^2) + (0 x 2^3) + (1 x 2^4) + (0 x 2^5) + (0 x 2^6) + (0 x 2^7) = 16 + 1 = 17。记住,从右到左阅读。
数字00110010是(0 x 2^0) + (1 x 2^1) + (0 x 2^2) + (0 x 2^3) + (**1** x 2^4) + (**1** x 2^5) + (0 x 2^6) + (0 x 2^7) = 32+16+2 = 50。
自己尝试使用序列00101010,以了解您是否了解并使用 Python 程序进行验证。
二进制数的逻辑运算
二进制左移和二进制右移
在二进制中,乘以因子 2 和除以因子 2 非常容易。 我们只需将位左移或右移。 我们向左下方移动:
| 位 4 | 位 3 | 位 2 | 位 1 |
|---|---|---|---|
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
在移位(0,1,0,1)之前,我们有数字 5。 移位(1,0,1,0)后,我们得到数字 10。在 python 中,您可以使用按位向左运算符(<<)向左移动,按位向右运算符(>>) 向右移动。
inputA = int('0101',2)print "Before shifting " + str(inputA) + " " + bin(inputA)print "After shifting in binary: " + bin(inputA << 1)print "After shifting in decimal: " + str(inputA << 1)
输出:
Before shifting 5 0b101After shifting in binary: 0b1010After shifting in decimal: 10
AND 运算符
给定两个输入,计算机可以使用这些位进行若干逻辑运算。让我们以 AND 运算符为例。 如果输入 A 和输入 B 为正,则输出将为正。 我们将以图形方式演示 AND 运算符,左边的两个是输入 A 和输入 B,右边的圆是输出:
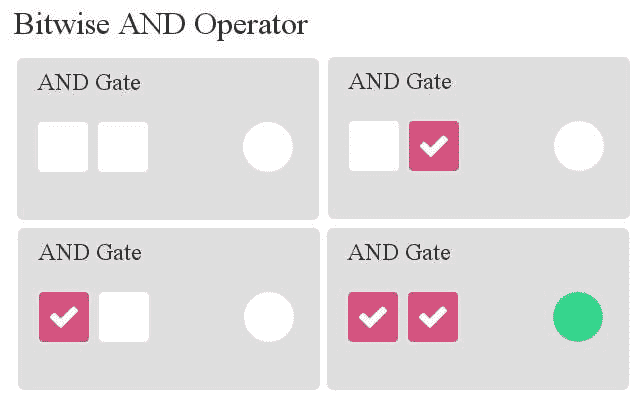
按位 AND
在代码中,这就像使用&符号一样简单,该符号代表逻辑 AND 运算符。
# This code will execute a bitwise logical AND. Both inputA and inputB are bits.inputA = 1inputB = 1print inputA & inputB # Bitwise AND
通过更改输入,您将获得与上图相同的结果。 我们可以对一个序列执行 AND 运算符:
inputA = int('00100011',2) # define binary sequence inputAinputB = int('00101101',2) # define binary sequence inputBprint bin(inputA & inputB) # logical AND on inputA and inputB and output in binary
输出:
0b100001 # equals 00100001
这是有道理的,因为如果您手动进行操作:
0010001100101101-------- Logical bitwise AND00100001
OR 运算符
现在您已经了解了 AND 运算符,让我们看一下 OR 运算符。 给定两个输入,仅当 A 和 B 均为零时,输出才为零。
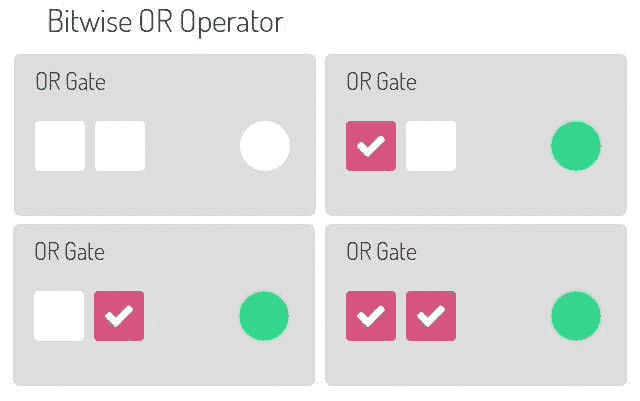
二进制按位 OR
要执行它,我们使用|运算符。 可以像这样简单地执行一系列位:
inputA = int('00100011',2) # define binary numberinputB = int('00101101',2) # define binary numberprint bin(inputA) # prints inputA in binaryprint bin(inputB) # prints inputB in binaryprint bin(inputA | inputB) # Execute bitwise logical OR and print result in binary
输出:
0b1000110b1011010b101111
XOR 运算符
这是一个有趣的运算符:异或或简称 XOR。
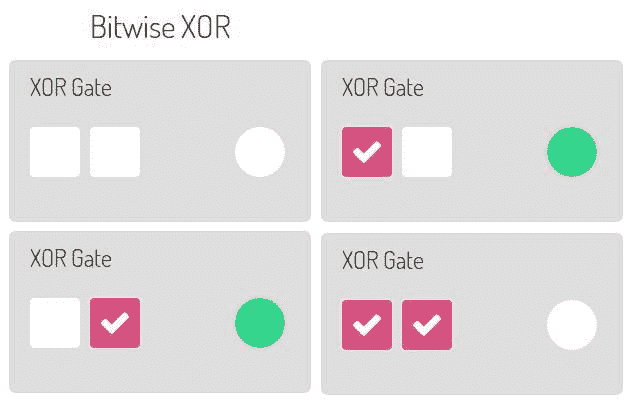
按位 XOR
为了执行它,我们使用^运算符。 可以像这样简单地执行一系列位:
inputA = int('00100011',2) # define binary numberinputB = int('00101101',2) # define binary numberprint bin(inputA) # prints inputA in binaryprint bin(inputB) # prints inputB in binaryprint bin(inputA ^ inputB) # Execute bitwise logical OR and print result in binary
输出:
0b1000110b1011010b1110

