题目

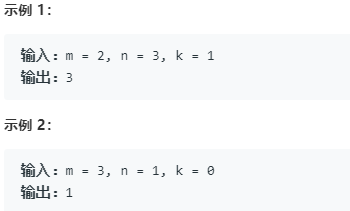
地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

image.png

思路

dfs，回溯法。

代码

  1. class Solution:
  2.     def movingCount(self, m: int, n: int, k: int) -> int:
  3.         visited=[[False for _ in range(n)] for _ in range(m)] #定义标记访问状态
  4.         return self.DFS(0,0,m,n,visited,k) #初始状态是原点
  6.     def DFS(self,i,j,m,n,visited,k):
  8.         if i<0 or i>=m or j<0 or j>=n or self.cal(i)+self.cal(j)>k or visited[i][j]==True: #边界条件
  9.             return 0
  11.         visited[i][j]=True
  12.         #回溯子状态
  13.         return 1+self.DFS(i-1,j,m,n,visited,k)+self.DFS(i,j-1,m,n,visited,k)+self.DFS(i+1,j,m,n,visited,k)+self.DFS(i,j+1,m,n,visited,k)
  16.     def cal(self,num): #计算行坐标和列坐标数位和
  18.         total=0
  19.         while num>0:
  20.             total+=num%10
  21.             num//=10
  22.         return total
  1. class Solution:
  2.     def movingCount(self, m: int, n: int, k: int) -> int:
  3.         def digit_sum(num):
  4.             tmp = 0
  5.             while num > 0:
  6.                 tmp += num % 10
  7.                 num //= 10
  8.             return tmp
  12.         vis = set([(0, 0)])
  13.         for i in range(m):
  14.             for j in range(n):
  15.                 if ((i - 1, j) in vis or (i, j - 1) in vis) and digit_sum(i) + digit_sum(j) <= k:
  16.                     vis.add((i, j))
  17.         return len(vis)