完全平方数

题目

https://leetcode-cn.com/problems/perfect-squares/
给定正整数n，找到若干个完全平方数（比如1， 4， 9， 16，……）使得他们的和等于n。你需要让组成和的完全平方数的个数最少。

思路

思路一：暴力枚举法

重点：枚举所有可能的组合，并找到完全平方数的个数最小的一个。
公式表述为：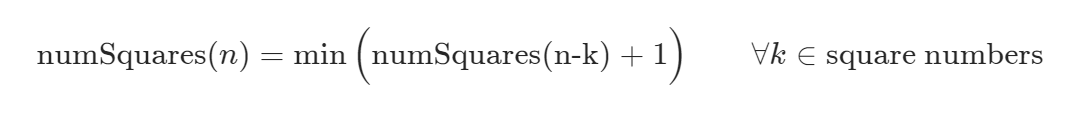

代码使用递归来实现。

n = int(input())
squre_nums = [i ** 2 for i in range(1, int(n ** 0.5 + 1)]
def minNumSquares(k):
    # 如果k恰好是一个平方数，直接返回
    if k in squre_nums: return 1
    min_num = float('INF')
    # 遍历所有可能的情况，找到最小的值
    for square in square_nums:
        if k < square: break
        new_num = minNumSquare(k - square) + 1
        min_num = min(min_num, new_num)
minNumSquares(n)

如果n较大，可能 由于过度递归，产生堆栈溢出。

思路二：动态规划

• 要计算numSquares(10)的值， 需要计算numSquares(10 - 1), numSquares(10 - 4), numSquares(10 - 9)的值；
• 要计算numSquares(10 - 9)的值，需要计算numSquares(10 - 1), numSquares(10 - 4)。
• ……

可以看出，中间结果被重复计算了多次。

因可以考虑使用一个变量—备忘录dp_table，保存中间结果。

class Solution:
    def numSquares(self, n: int) -> int:
        square_nums = [i ** 2 for i in range(0, int(n ** 0.5) + 1)]
        dp = [float('INF')] * (n + 1) # 表示组成和为i的完全平方数的个数最少是dp[i]
        dp[0] = 0
        for i in range(1, n+1):
            for num in square_nums:
                if i < num: break
                dp[i] = min(dp[i], dp[i - num] + 1)
        return dp[-1]

思路三：BFS（广度优先搜索）

广度优先搜索就是一颗N元树，一层一层地搜索。
那么节点（num，step）代表给定正整数num，需要step个完全平方数的和能组成num。
对于当前节点，其子节点为：[number - ii for i in range(1, int(number*0.5)+1)]

class Solution:
    def numSquares(self, n: int) -> int:
        from collections import deque
        queue = deque()
        visited = set()
        queue.append((n, 0))
        while queue:
            number, step = queue.popleft()
            targets = [number - i*i for i in range(1, int(number**0.5)+1)]
            for target in targets:
                if target == 0: return step + 1
                if target not in visited:
                    queue.append((target, step + 1))
                    visited.add(target)
        return 0