题目

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

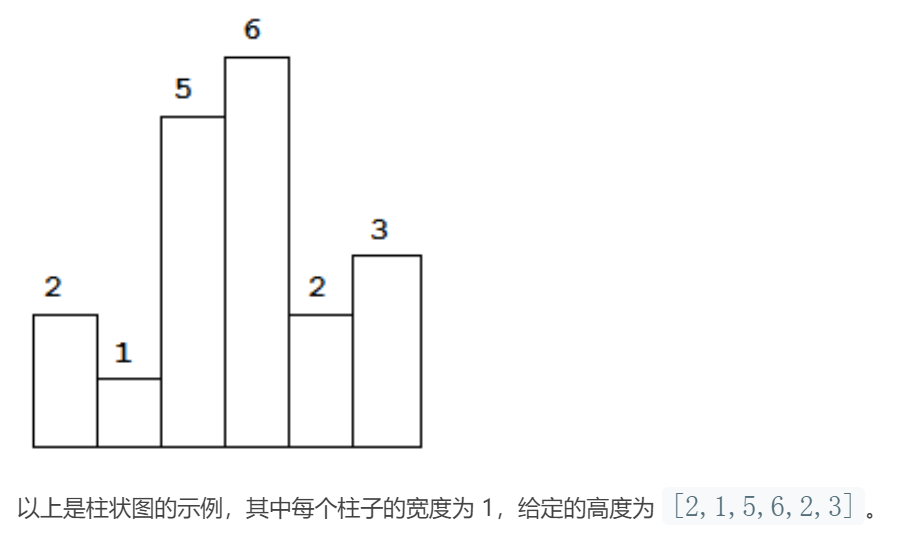
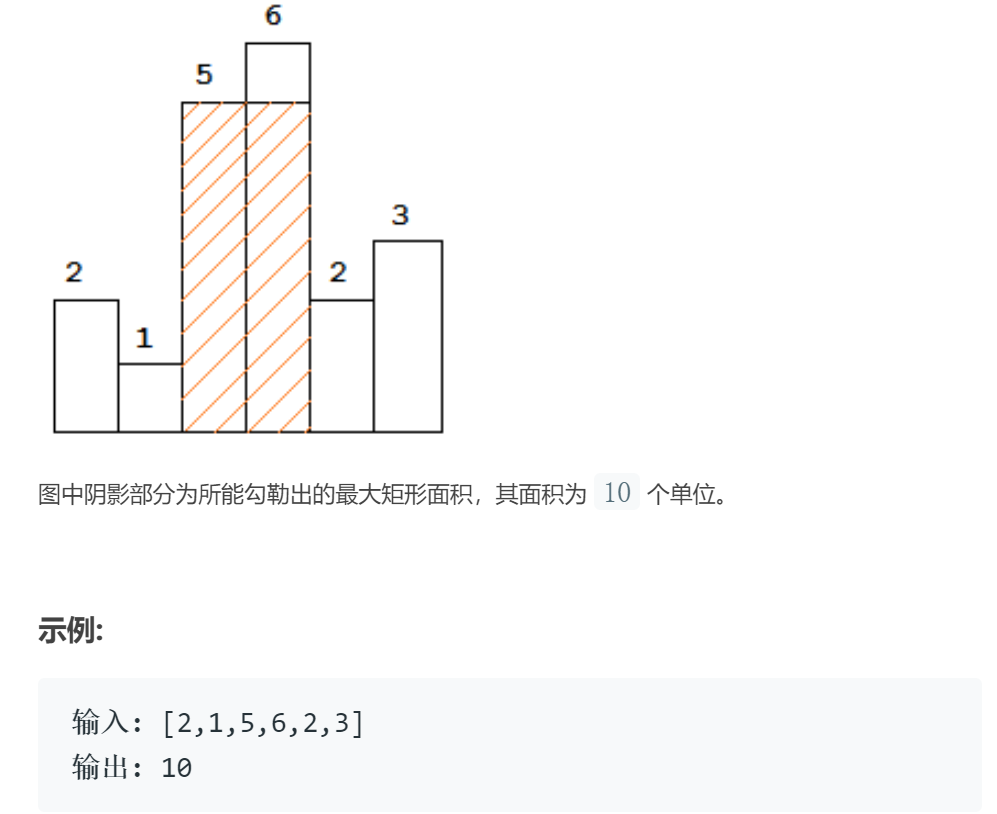
image.png
image.png

思路

思路一：
暴力搜索。两层循环，分别确定左边界和右边界。

  1. class Solution:
  2.     def largestRectangleArea(self, heights: List[int]) -> int:
  3.         # 暴力法
  4.         # 枚举左边界
  5.         # 枚举右边界
  6.         length = len(heights)
  7.         max_area = 0
  8.         for i in range(length):
  9.             for j in range(i, length):
  10.                 area = (j - i + 1) * min(heights[i:j+1])
  11.                 max_area = max(max_area, area)
  13.         return max_area

最大时间复杂度：【LeetCode】84.柱状图中最大的矩形 - 图3
有两个测试样例没通过…

如果我们枚举「高」，我们可以使用一重循环枚举某一根柱子，将其固定为矩形的高度 h。随后我们从这跟柱子开始向两侧延伸，直到遇到高度小于 h 的柱子，就确定了矩形的左右边界。如果左右边界之间的宽度为 w，那么对应的面积为 w * h。

  1. class Solution:
  2.     def largestRectangleArea(self, heights: List[int]) -> int:
  3.         n = len(heights)
  4.         max_area = 0
  6.         for mid in range(n):
  7.             left = right = mid
  9.             # 找到mid左边小于heights[mid]的前一个
  10.             while left >= 0 and heights[left] >= heights[mid]:
  11.                 left -= 1
  13.             # 找到mid右边小于heights[mid]的前一个
  14.             while right < n and heights[right] >= heights[mid]:
  15.                 right += 1
  17.             max_area = max(max_area, heights[mid]*(right - left - 1))
  19.         return max_area

最大时间复杂度还是【LeetCode】84.柱状图中最大的矩形 - 图4。

https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/ji-jian-python-shen-du-jie-xi-dan-diao-dui-zhan-zu/

代码

  1. class Solution:
  2.     def largestRectangleArea(self, heights: List[int]) -> int:
  3.         stack = [-1]
  4.         max_res = 0
  5.         for i in range(len(heights)):
  6.             while len(stack) > 1 and heights[i] <= heights[stack[-1]]:
  7.                 max_res = max(max_res, heights[stack.pop()] * (i - stack[-1] - 1))  
  8.             stack.append(i)
  9.         for i in range(len(stack)-1):
  10.             max_res = max(max_res, heights[stack.pop()]*(len(heights)-1-stack[-1]))
  11.         return max_res
  13. 作者：allen-238
  14. 链接：https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/ji-jian-python-shen-du-jie-xi-dan-diao-dui-zhan-zu/
  15. 来源：力扣（LeetCode）
  16. 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
  1. class Solution:
  2.     def largestRectangleArea(self, heights: List[int]) -> int:
  3.         n, heights, st, ans = len(heights), [0] + heights + [0], [], 0
  4.         for i in range(n + 2):
  5.             while st and heights[st[-1]] > heights[i]:
  6.                 ans = max(ans, heights[st.pop(-1)] * (i - st[-1] - 1))
  7.             st.append(i)
  8.         return ans