想让计算机能够自动的分析语言，就要把语言学知识，也就是文法，告诉他。那么怎么表示语言及文法呢？

基本概念

字母表：
image.pngimage.png
字母表上的运算：乘积、次幂、正闭包，克林闭包。具体规则看书吧。
image.pngimage.png
image.pngimage.png
串
image.png
串上的运算：连接、幂运算
image.pngimage.png

文法的定义

是用来做什么的？
文法是用来描述句子的构成规则的
为什么需要他？
因为句子是无穷的，但是构成句子的规则却是一定的，所以我们可以定义组成句子的规则，即文法。进而组成句子。
他是怎么解决问题的？
暂不清楚。
他是啥？
其形式化定义是：
image.png
比如上例中，apple就是一个终结符（token）。整个 Vt是终结符集
解释：词法单元才是token，token=。这里tokenname可以理解成终结符。
image.png
比如上例中，由于可以从 句子或者名词短语中 进一步分成出其他的语法成分，所以他们就叫做非终结符
image.png
产生式：简而言之，就是产生串的方法
image.png
例如，在上面的例子中，每一条规则都是一个产生式
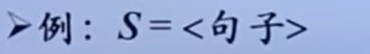
image.png
image.png
例如，句子就这个文法的开始符号

对终结符集和非终结符集，有：
image.png
image.png image.png
这里基本符号就是单词
而如果一个文法用来描述单词的构成规则的话，那么基本符号就应该是字母。

一个文法的例子：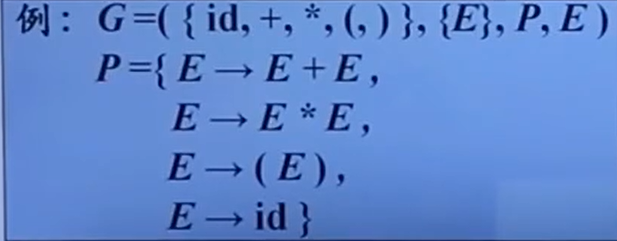
image.png
上面是一个简化的、来表示算术表达式的文法。 在这个文法中，
有终结符集合，非终结符（只有一个E），
由于他是一个描述表达式的文法，所以表达式就是最大的语法成分，即开始符号
image.pngimage.pngimage.pngimage.pngimage.png

终结符、非终结符表示小结

image.png

语言的定义

有了文法，如何判定一个词串是否是满足文法的句子？

推导、规约

image.png
image.png

句型和句子

image.png
例子：
image.png只有最后一个被称之为句子，因为只有最后一个没有 非终结符

语言

作用是什么？不知
为什么需要他？不知
怎么起作用的？不知
是什么？
第二章：语言及其文法 - 图30
问题答案：包含无限个。
上面这个算数表达式文法生成的语言中包含无数个句子
所以可以说文法解决了无穷语言的有穷表示问题

举个例子：
image.png
这是一个文法，那么这个文法生成的语言是什么？
（首先这为什么是个文法？很明显是简写：只写了产生式）
看第4个产生式，说明D是数字（digit）、看第3个产生式，说明L是字母。
先让T推导，最后能推导出如下结果：即推导出来的是字母数字串。
image.png
再用S推导，推出LT，所以S推出的应该是 字母打头的字母数字串。 而这正是标识符的定义。
所以该文法最后推出来的语言是标识符。

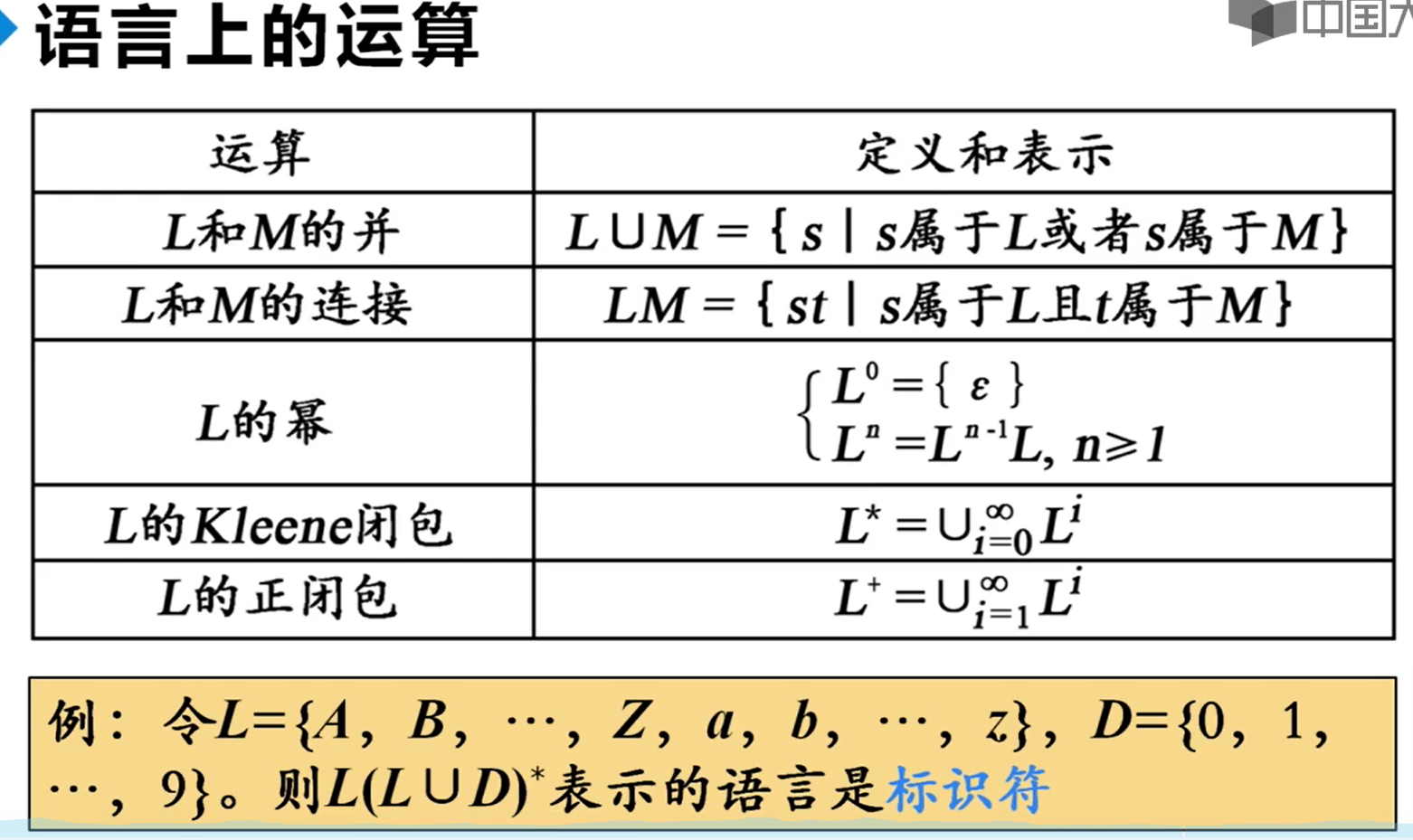
语言上的运算

第二章：语言及其文法 - 图33

文法的分类

image.png
image.png

CFG的分析树

俩文法：
正则文法描述大部分词语，但是没法描述句子结构
上下文无关文法可以描述句子结构。

上下文无关文法推导句子结构的过程的图形化显示就是分析树。
分析树：
根节点、内部节点、叶子节点（产出、边缘）
短语：每个子树的边缘
直接短语：高度为2的子树的边缘

二义文法

比如 if then A if then B else C
有歧义，else不知道归属于哪个if

怎么判断二义文法？没有相关算法，只有一个充分条件（满足，肯定无二义性；不满足，未必有二义性）

词法分析：正则表达式、有穷自动机（FA）、DFA与NFA及RE的相互转换、DFA识别单词、语法检测

词法分析：正则表达式

正则表达式可以更好的描述 语言。
语言：语言是字母表上的一个串集。属于该语言的串是该语言的句子或字。一个语法正确的C程序的集合是语言、所有语法正确的英语句子集合也是语言、空串也符合（是抽象语言）
字母表：比如二进制字母表 {0，1} Unicode字母表 {a,b,c…..}
串：字母表几个字符组成的集合。 比如banana就是长度为6的串。 对串s， |s| 就是串的长度。
串的运算：连接、和、闭包。
连接：写作ss，就是两个s拼到一块
和：就是并集，L U M = { s| s属于L或者s属于M }
闭包：分成闭包（也叫克林闭包）和正闭包，闭包可以是0到无穷个。 正闭包是1到无穷个。

两个正则表达式的运算：
image.png

正则语言：即，RE（正则表达式）定义的语言，也叫正则集合

正则表达式RE的代数规律：交换、结合、分配、幂等

正则文法：等价于正则表达式

正则定义

就是一个过程，不用记。 就是给一些RE命名，并在之后可以使用这些名字。 命名的过程就是正则定义。
下面是例子：
image.png

词法分析的理论基础：有穷自动机（FA）

FA是一种数学模型
有：一系列离散的输入输出，有穷数目的内部状态（内部状态就是：对过去输入的处理情况的概括）

典型例子：
电梯
输入：用户的选择的层数
状态：当前所处层数、运动方向

模型：输入带、读头、有穷控制器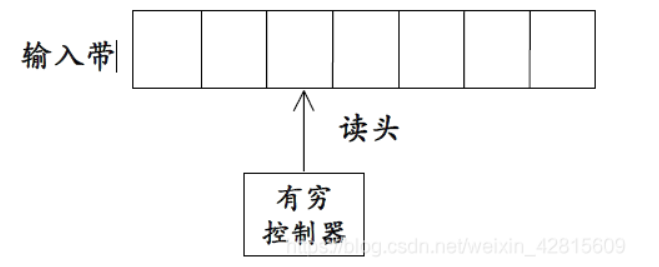
image.pngimage.png

转换图

节点：FA的状态、开始状态（start）、终止状态（双圈）、状态转换（有向边）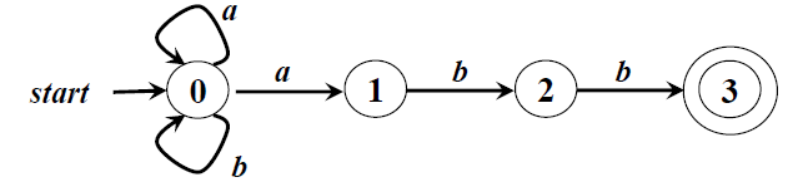
image.png

FA接受的语言L(M)

从开始状态到终止状态的转换序列。
m是machine的意思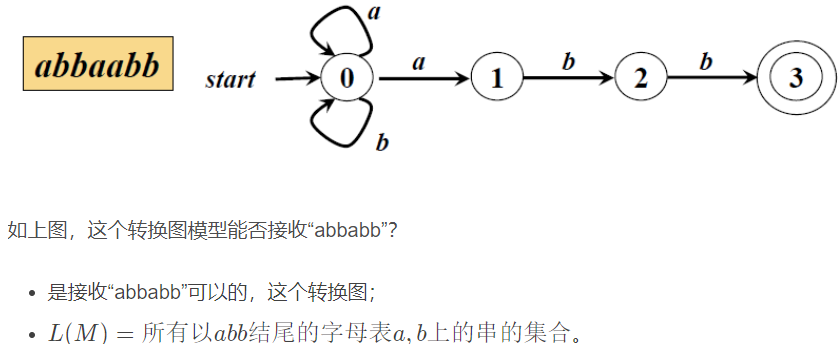
image.png

最长匹配原则

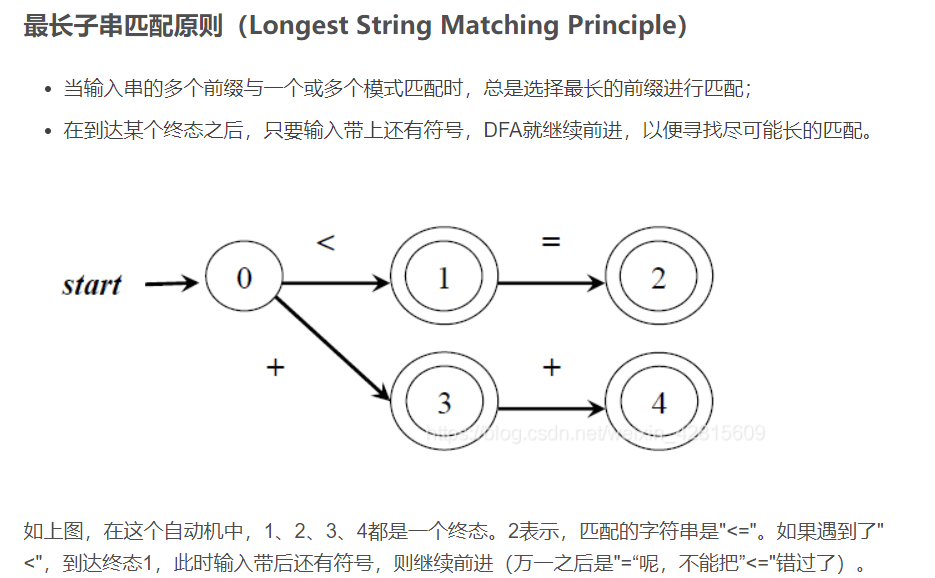
image.png

FA分类

两类：
确定的有穷自动机（DFA）
非确定的有穷自动机（NFA）

DFA是一个五元组
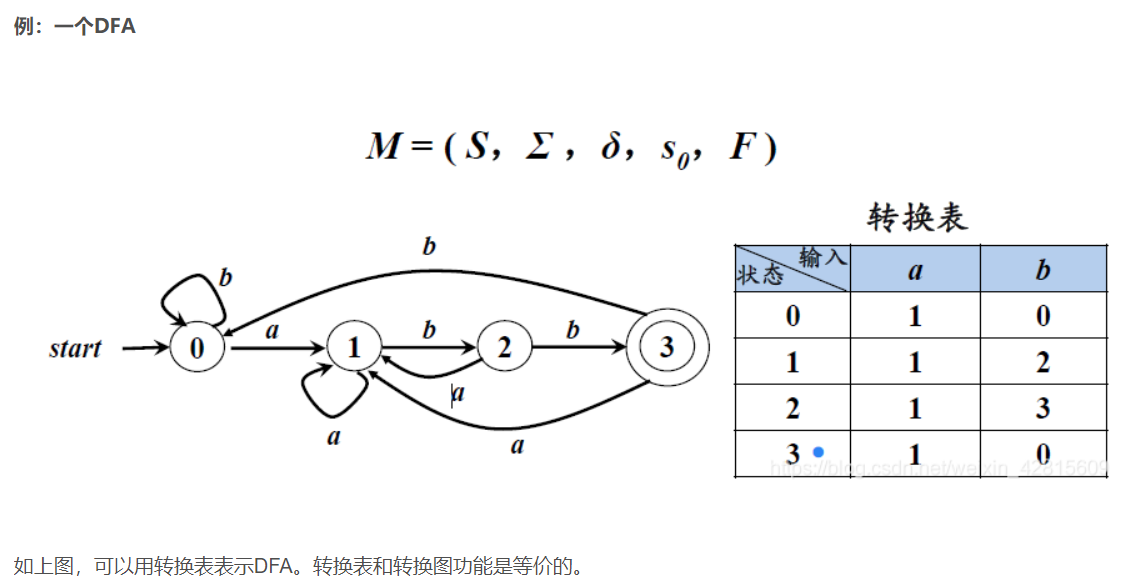
image.png
image.png

非确定有穷自动机
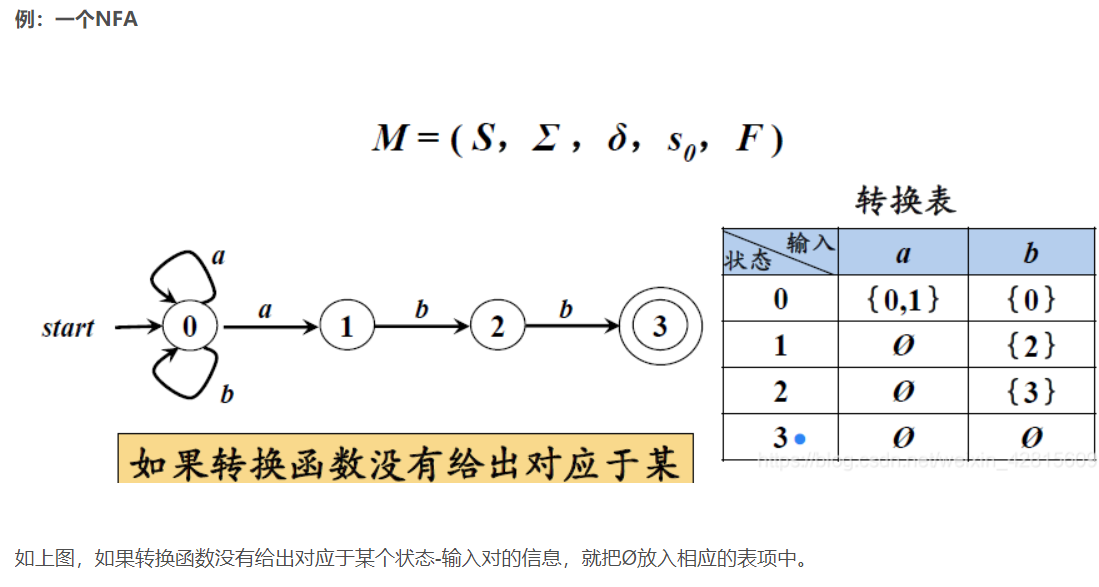
image.pngimage.png

DFA和NFA等价
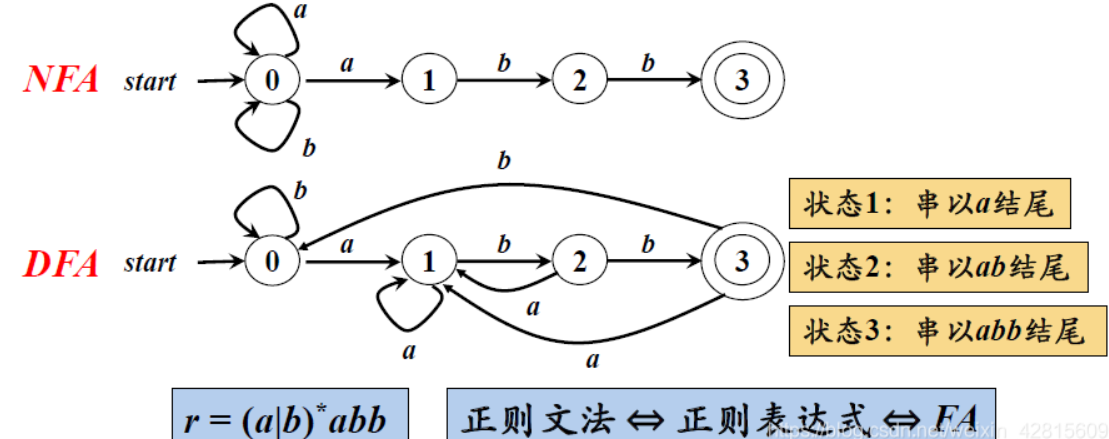
image.pngimage.pngimage.png

正则文法⇔正则表达式⇔FA

带有”ϵ - 边”的NFA，和不带”ϵ - 边”的NFA是等价的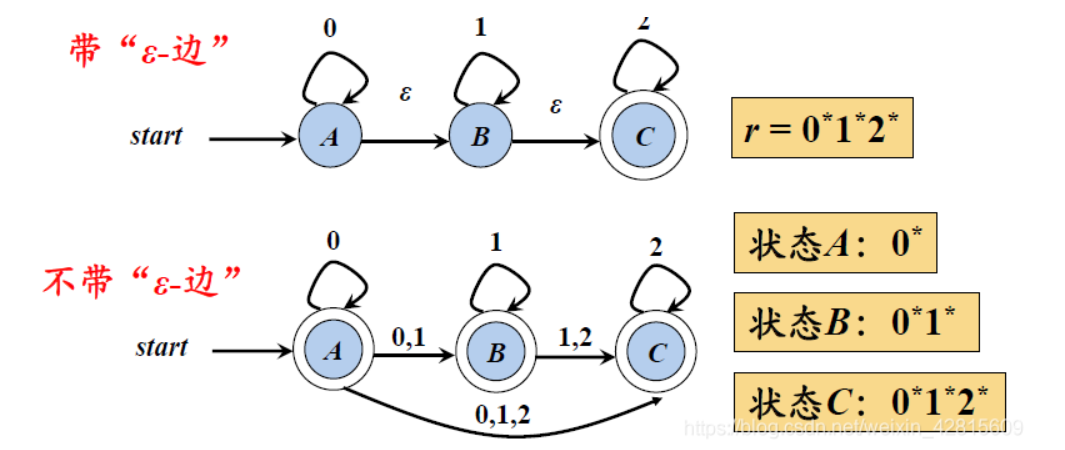
image.png

从正则表达式到DFA

上面说了正则表达式和FA等价，所以肯定可以相互转化。
具体的转化过程看CSDN笔记吧。这里不写了。 总之需要先转化成 NFA，再由NFA转化成DFA

DFA一个状态代表NFA多个状态

识别单词的DFA

DFA可以识别 标识符、无符号数、各进制无符号整数、注释、Token
每个都有识别自己的DFA。
（DFA是啥？用图的话，不就是start、终止符号、有向边这些组成的图嘛）
比如识别标识符的DFA如下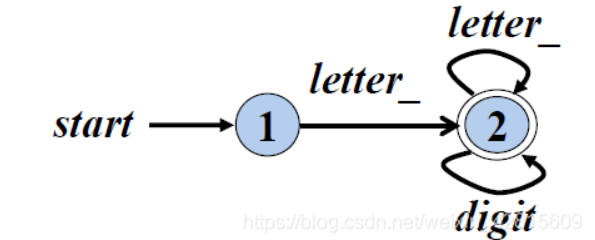
image.png

词法分析阶段的错误处理

还有词法错误检测机制、词法分析的错误处理、错误恢复策略。