题目描述

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个非递减排序的数组的一个旋转，输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。
NOTE：给出的所有元素都大于0，若数组大小为0，请返回0。

方法一

一、分析

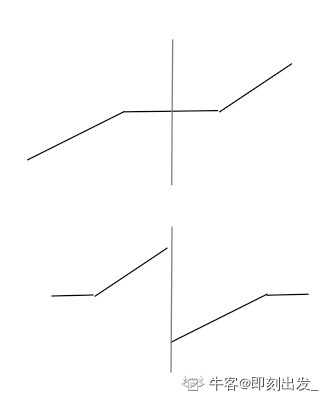
下图中上面的曲线可以看做原数组，从竖线处切分后，得到下面的图。我们的目标就是找那个最低点

第六题 旋转数组的最小数字 - 图1
计算数组是排序的，再线性地查找就显得不高效了。排序数组，自然要想到二分查找。只是这里的操作和常规二分查找不同。
二分查找的 mid 如果落在左半边，那么就 lo=mid+1，如果落在右半边，就减小 hi=mid。不断缩小范围，最终，lo 一定会掉到最低点。
但是要如何判断 mid 落在那一边呢。因为左半边 >= 右半边，如果原数组是严格递增的，你可以说，当 a[mid] > a[0] 那就是左半边。但是考虑下面这幅图：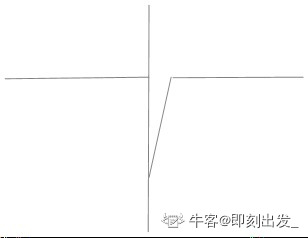
第六题 旋转数组的最小数字 - 图2
如果原数组只有开始部分递增，之后很长一段都是平坦的，那么旋转后可能是上图的样子。a[mid] == a[lo] == a[hi]，根本没法判断 mid 在那边。解决的方法很简单

  1. while(a[lo] == a[hi]){
  2.     ++lo;
  3.     --hi;
  4. }

这样操作以后，一定有 a[lo] > a[hi]，一旦 lo 掉到了最低点，这个条件就不成立了。判断 mid 在左在右也很简单了，如果 a[mid] >= a[lo] 那就是左边。如果 a[mid] <= a[hi] 那就是右边。
如果在左边，那就 lo=mid+1，这样把 lo 向右边推进。如果在右边，为了避免 hi 爬到了左边去 hi=mid 即可。最终终止条件，就是 lo 落到了最低点。

二、代码1

  1. class Solution {
  2. public:
  3.     int minNumberInRotateArray(vector<int> a) {
  4.         if (a.size() == 0) return 0;
  6.         int lo = 0, hi = a.size()-1;
  8.         while(a[lo] == a[hi]){
  9.             ++lo;
  10.             --hi;
  11.         } 
  12.         while(a[lo] > a[hi]){
  13.             int mid = lo + (hi-lo) / 2;
  15.             if(a[mid] >= a[lo]){
  16.                 lo = mid + 1;
  17.             }else if(a[mid] <= a[hi]){
  18.                 hi = mid;
  19.             }
  20.         }
  22.         return a[lo];
  23.     }
  24. };

三、代码2

  1. public static int minNumberInRotateArray(int[] array) {
  2.         if (array.length == 0)
  3.             return 0;
  4.         int left = 0;
  5.         int right = array.length - 1;
  6.         int middle = -1;
  7.         while (array[left]>=array[right]) {
  8.             if(right-left==1){
  9.                 middle = right;
  10.                 break;
  11.             }
  12.             middle = left + (right - left) / 2;
  13.             if (array[middle] >= array[left]) {
  14.                 left = middle;
  15.             }
  16.             if (array[middle] <= array[right]) {
  17.                 right = middle;
  18.             }
  19.         }
  20.         return array[middle];
  21.     }

方法二

一、分析

基于暴力遍历的方法优化

二、代码

  1. public int minNumberInRotateArray(int[] array) {
  2.         if (array.length == 0)
  3.             return 0;
  4.         for (int i = 0; i < array.length - 1; i++) {
  5.             if (array[i] > array[i + 1])
  6.                 return array[i + 1];
  7.         }
  8.         return array[0];
  9.     }