34 数组中的逆序对

题目描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

思想:

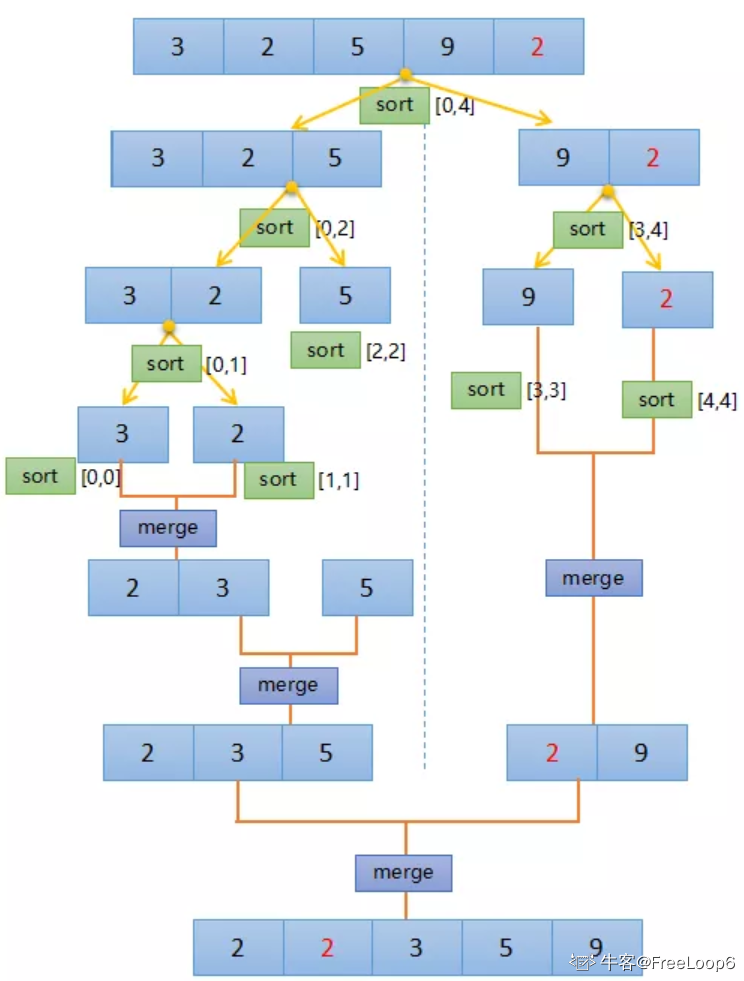
通过归并的思想,在不断归并过程中统计逆序对的个数

• 在数组分裂的过程中，把left和right从第i个位置开始进行比较，哪个小就把它加入merged中，由于此时left和right是分别有序的，如果left[i]>right[j]，证明left[i:]都大于right[j]，此时的逆序对要加len(left)-i
  
• 例如，left = [5, 7], right = [4, 6]
  1. i = 0, j = 0, 5>4, 此时5和7都是大于4的，逆序对加2-0=2, merged = [4]
     
  2. i = 0, j = 1, 5<6, 此时无逆序对，merged = [4, 5]
     
  3. i = 1, j = 1, 7>6, 逆序对加2-1=1，merged = [4, 5, 6]
     
  4. merged = [4, 5, 6, 7]
     

代码

public class Solution {
    static int count=0;
     static int mod = (int) 1e9 + 7; 
    public static void main(String[] args)
    {
        int[] arr = new int[] {1,2,3,4,5,6,7,0};
        mergeSort(arr,0,arr.length-1);
        System.out.println(count);
    }
    public static void mergeSort(int[] arr,int left,int right) {
        if(arr.length==0)return;
        if(left==right)return;
        int mid = left+(right-left)/2;
        mergeSort(arr,left,mid);
        mergeSort(arr,mid+1,right);
        merge(arr,left,mid,right);
    }
    public static void merge(int[] arr,int left,int mid,int right) {
        //用来存放归并的数
        int i=0;
        int[] temp = new int[right-left+1];
        //在归并的过程中统计逆序对
        int lp=left;
        int rp=mid+1;
        //逆序对个数
        while(lp<=mid&&rp<=right)
        {
            if(arr[lp]>arr[rp]) {
                count += (mid-lp+1);
                count = count%mod;
                temp[i++]=arr[rp++];
            }else
            {
                temp[i++]=arr[lp++];
            }
        }
        while(lp<=mid)
        {
            temp[i++]=arr[lp++];
        }
        while(rp<=right)
        {
            temp[i++]=arr[rp++];
        }
        for(int j=0;j<temp.length;j++)
        {
            arr[left++] = temp[j];
        }
//        return count;
    }
}