线性结构难以胜任既要求对象集合的组成可以高效率地动态调整，同时也要求能够高效率地查找。

1. 查找

1.1 循关键码访问

与此前的“循秩访问” 和“循位置访问” 等完全不同， 这一新的访问方式， 与数据对象的物理位置或逻辑次序均无关。实际上，查找的过程与结果，仅仅取决于目标对象的关键码，故这种方式亦称作循关键码访问。如：根据身份证号查找特定公民，根据车牌号查找特定车辆。

2. 二叉搜索树

2.1 顺序性

任一节点r的左子树中，所有节点均不大于r。
任一节点r的右子树中，所有节点均不小于r。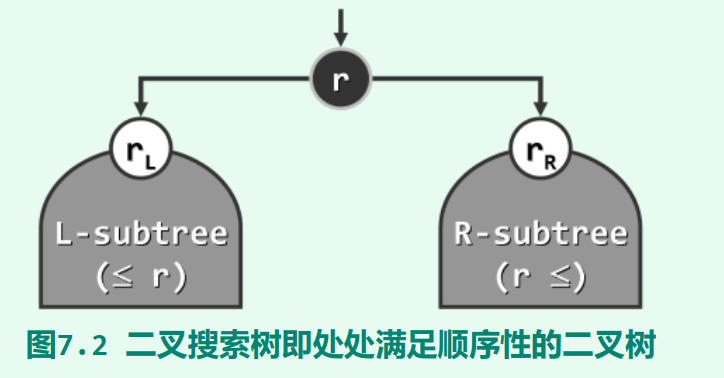
image.png

2.2 中序遍历序列

任何一棵二叉树是二叉搜索树，当且仅当其中序遍历序列单调非降。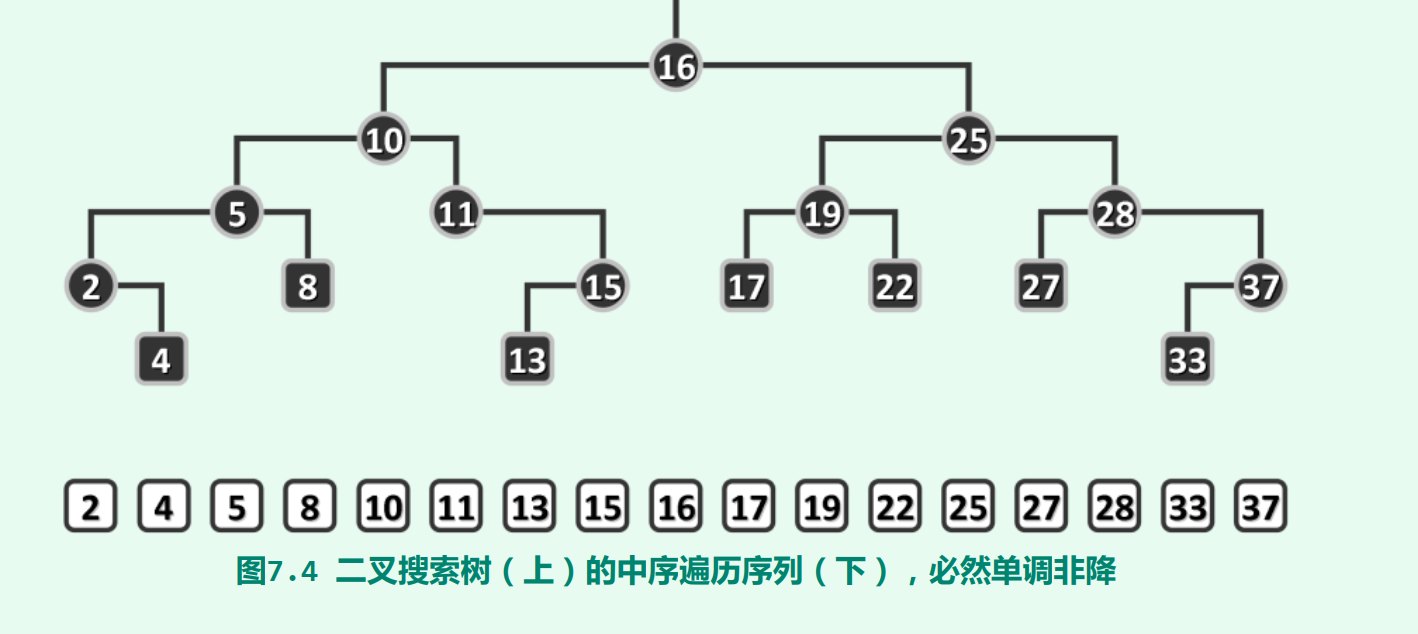
image.png

2.3 BST模版类

2.4 查找算法及其实现

从树根出发，逐步地缩小查找范围，直到发现目标（成功）或缩小至空树（失败）。

2.5 插入算法及其实现

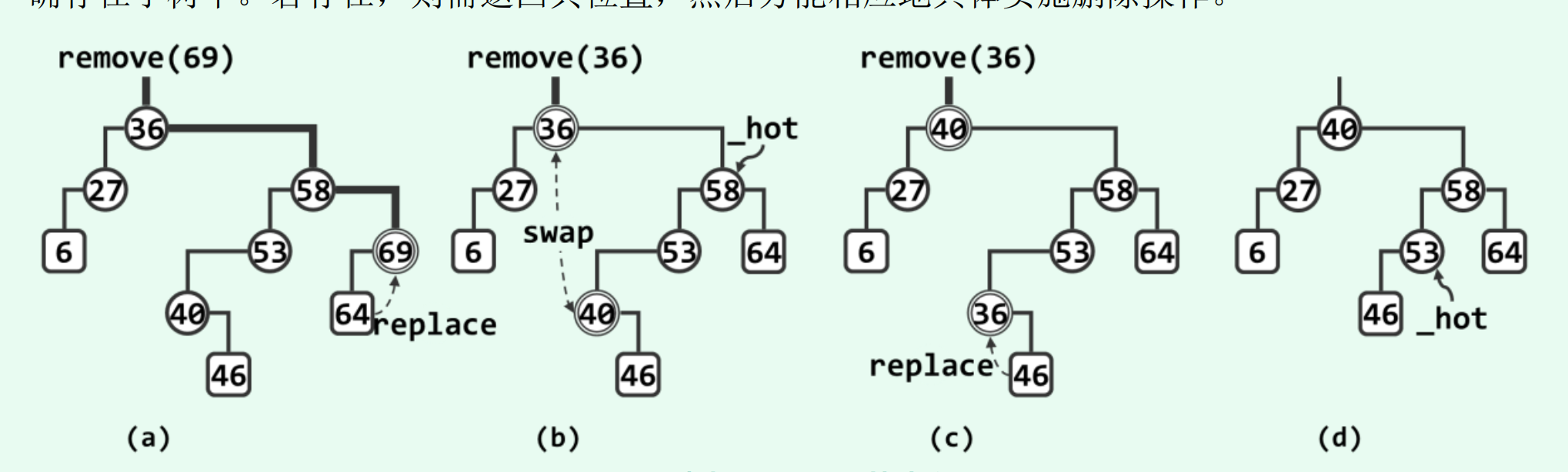
2.6 删除算法及其实现

image.png

3. 平衡二叉树

3.1 树高与性能

二叉搜索树中的查找、插入、删除等主要接口的运行时间，均线性正比于二叉搜索树的高度。在最坏情况下， 二叉搜索树可能彻底地退化为列表。

3.2 理想平衡与适度平衡

image.png

3.3 等价变换

3.3.1 等价二叉树搜索树

若两棵二叉搜索树的中序遍历序列相同，则称它们彼此等价；反之亦然。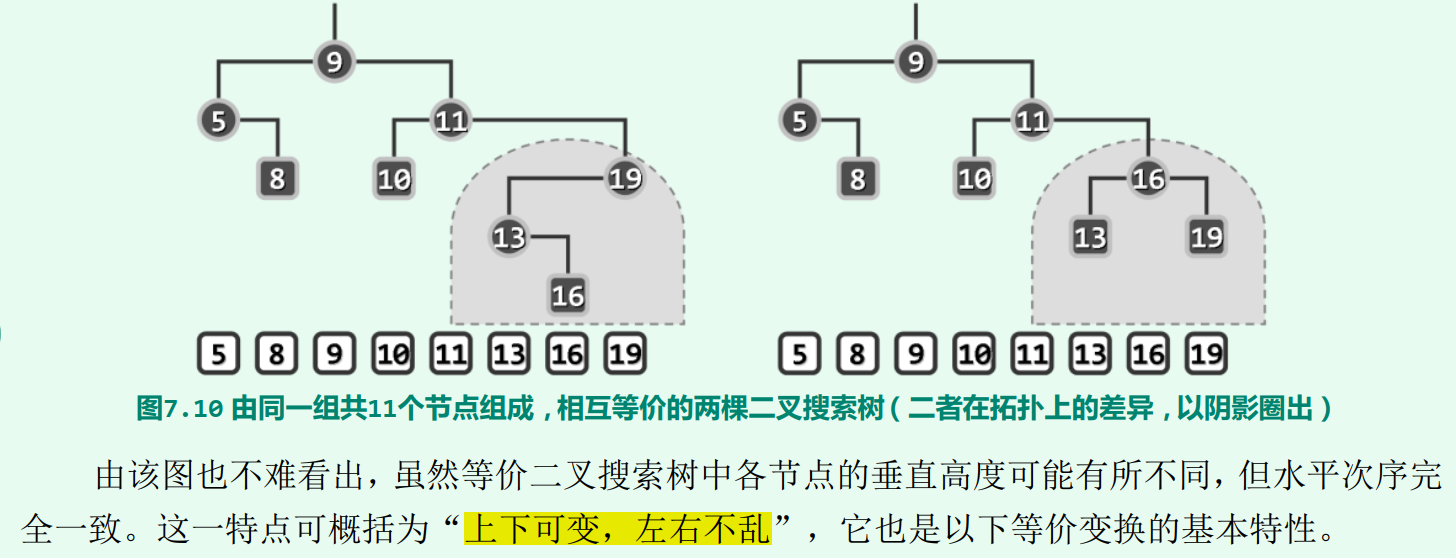
image.png

3.3.1 局部性

平衡二叉搜索树的适度平衡性，都是通过对树中每一局部增加某种限制条件来保证的。通常具有如下局部性：
image.png

3.4 旋转调整

旋转有两个主要的属性：旋转轴和旋转方向。
旋转轴：旋转轴即是原最小树经过旋转修正后的符合AVL的最小树的根节点。
旋转轴的确定：单旋转为不满足AVL条件的最小的树根的相应孩子节点，多旋转为不满足AVL条件的最小树根的相应孙子节点。
最基本的修复手段，就是通过围绕特定节点的旋转，实现等价前提下的局部拓扑调整。

3.4.1 左旋（zag）逆时针操作

将节点v的右子节点c”往上提”，节点v和v的左子树成为c的左子树，节点c原来的左子树成为节点v的右子树。

3.4.2 右旋（zig）顺时针操作

将节点v的左子节点c”往上提”，节点v和v的右子树成为c的右子树，节点c原来的右子树成为节点v的左子树。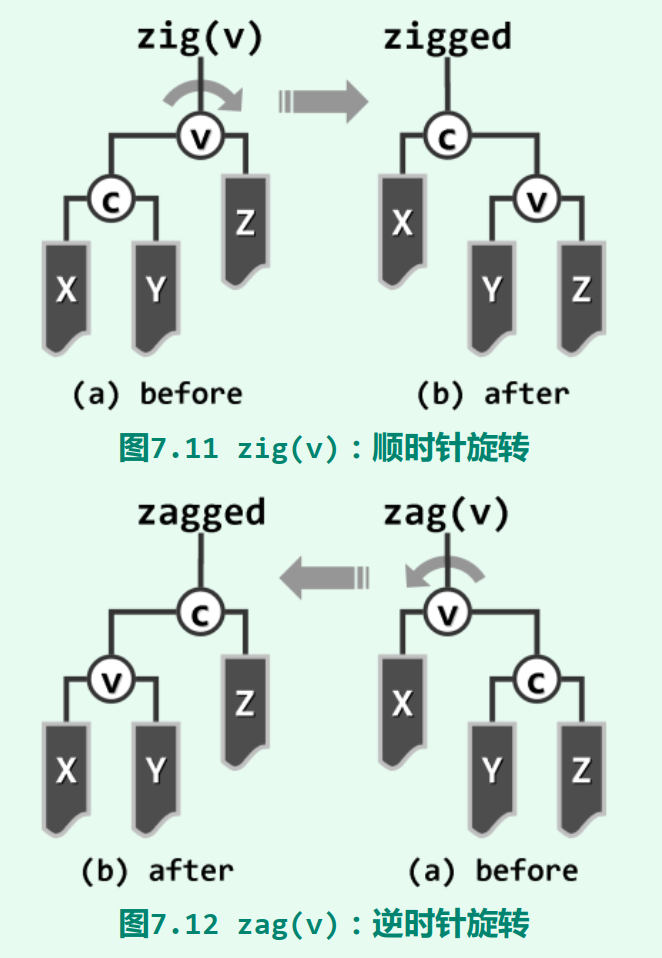
image.png
就与树相关的指标而言，经一次zig或zag旋转之后，节点v的深度加一，节点c的深度减一，这一局部子树（乃至全树） 的高度可能发生变化，但上、下幅度均不超过一层。

3.4.3 什么时候需要单旋转，什么时候需要多旋转

节点的插入有以下情形：

  1. 对α的左儿子的左子树进行一次插入。
  2. 对α的左儿子的右子树进行一次插入。
  3. 对α的右儿子的左子树进行一次插入。
  4. 对α的右儿子的右子树进行一次插入。

单旋转
LL型
双旋转

4. AVL树

自平衡二叉搜索树，在渐进意义下， AVL树可始终将其高度控制在O(logn)以内，从而保证每次查找、插入或删除操作， 均可在O(logn)的时间内完成。
特点：兄弟节点的高度相差不超过1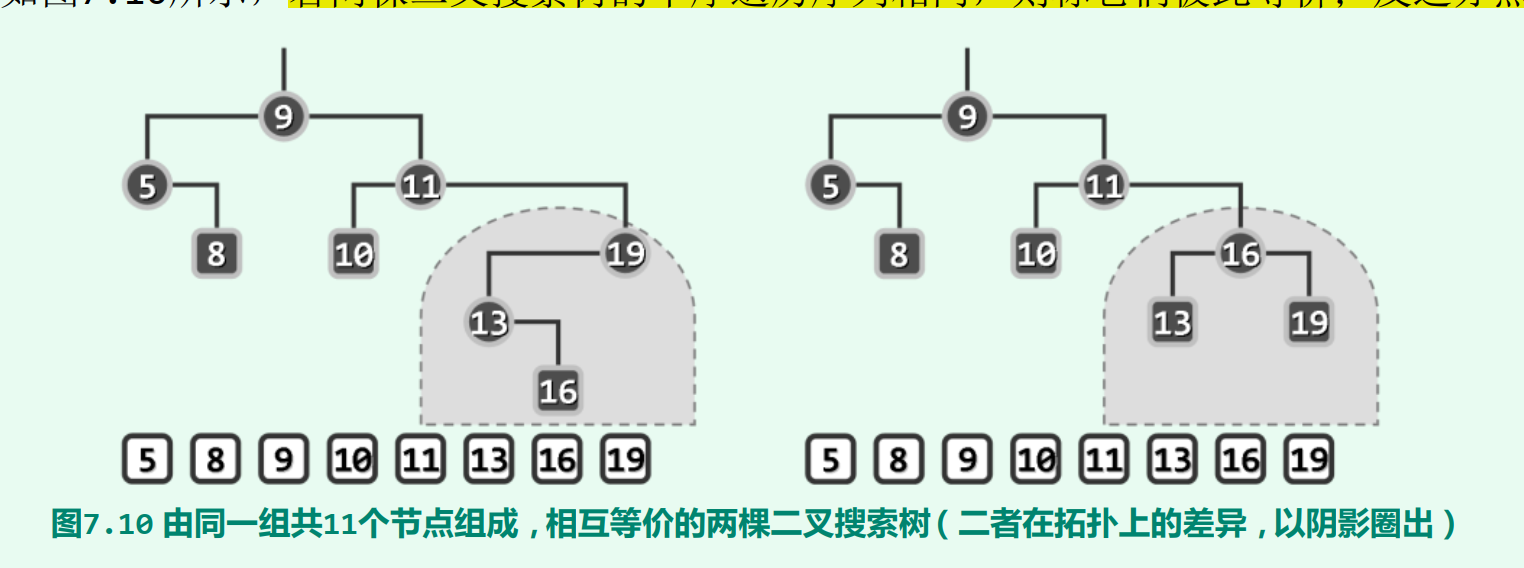
image.png

4.1 定义及性质

4.1.1 平衡因子

任一节点v的平衡因子（ balance factor） 定义为“其左、右子树的高度差” 。空树高度为-1，单节点子树的高度为0。所谓AVL树，即平衡因子受限的二叉搜索树，其中各节点平衡因子的绝对值均不超过1

4.1.2 平衡性

在完全二叉树中各节点的平衡因子非0即1，故完全二叉树必是AVL树。

4.1.3 失衡与重平衡

AVL树与常规的二叉搜索树一样，也应支持插入、删除等动态修改操作。 但经过这类操作之后，节点的高度可能发生变化，以致于不再满足AVL树的条件。
如此因节点x的插入或删除而暂时失衡的节点，构成失衡节点集，记作UT(x)。 请注意，若x为被摘除的节点，则UT(x)仅含单个节点；但若x为被引入的节点，则UT(x)可能包含多个节点。

4.2 节点插入

在AVL树中插入新节点后，仅需不超过两次旋转， 即可使整树恢复平衡。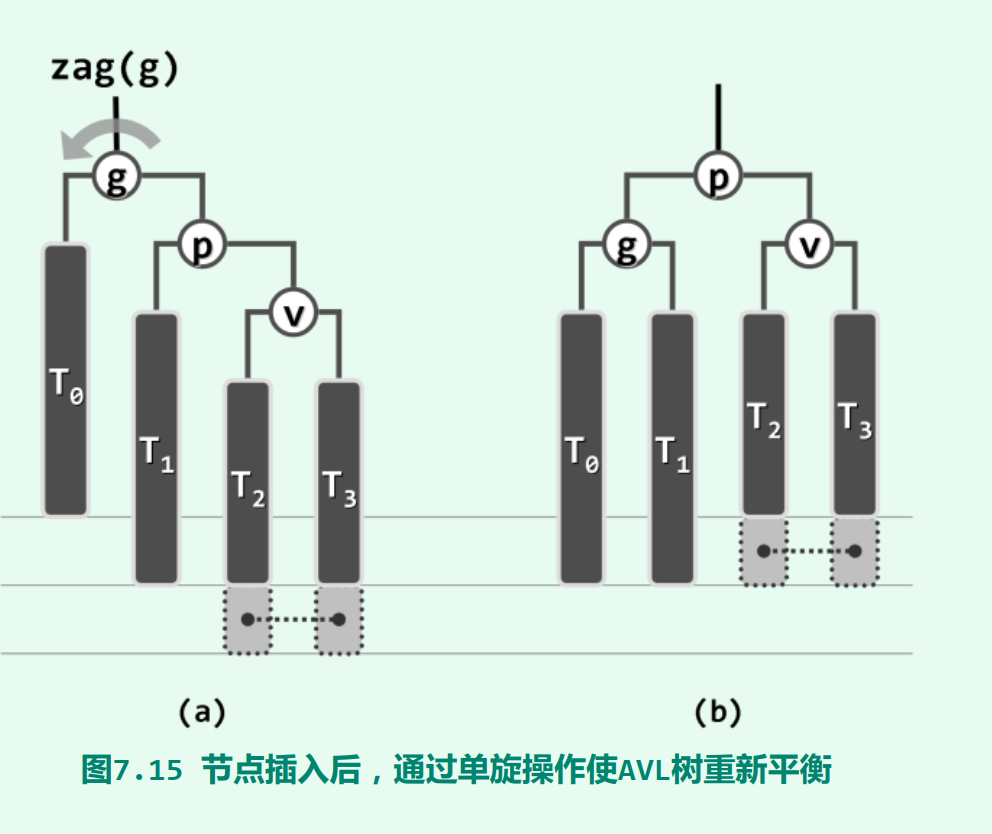
image.png
image.png

4.2.1 单旋

1:右旋（zig）顺时针操作 (左子树>右子树)
假设以下节点3是新插入的节点，那么树的平衡性就被打破了。找离新插入的节点最近的不平衡的树进行调整，节点7的左子树的高度比右子树的高度大2，所以需要对节点7进行右旋zig顺时针操纵。因为节点7的左子树高度更高，所以需要向上提高一下降低高度。节点5变成了轴点，节点7围着节点5进行zig操作。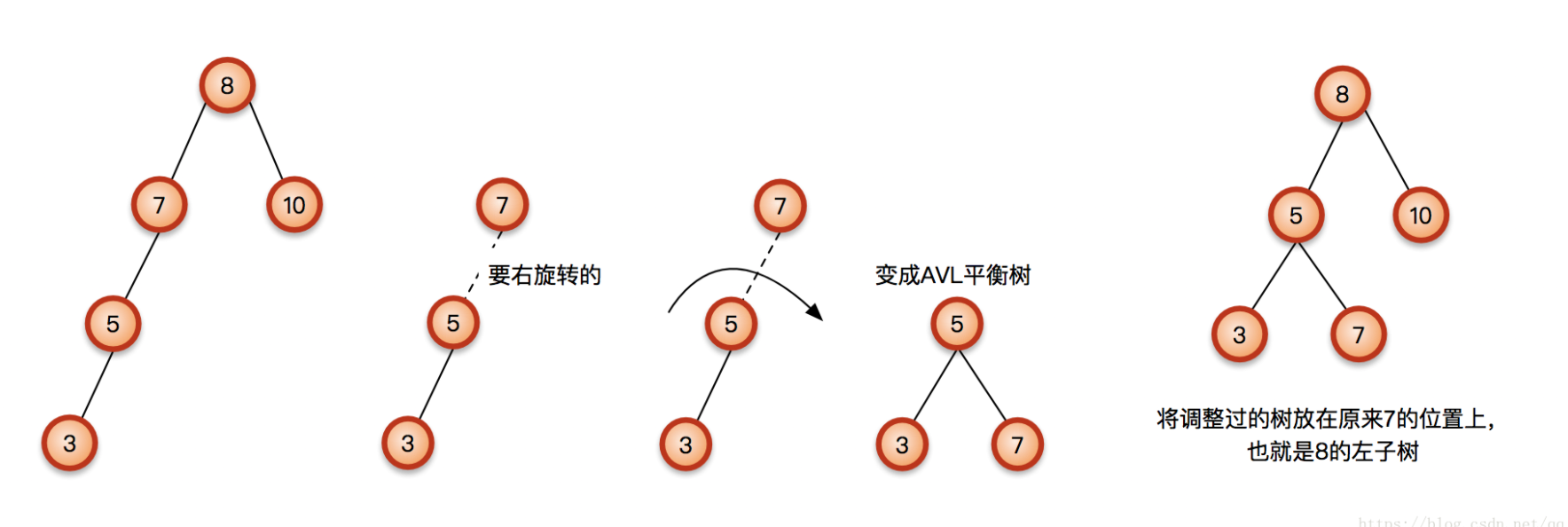
image.png
那如果节点5本来就有了右子树呢？照样右旋转，只要把原来5的右子树变成旋转后的7的左子树就行了。因为5的右子树肯定比5大，但是也肯定比7小的。（备注：下面这张图需要进行双旋操作）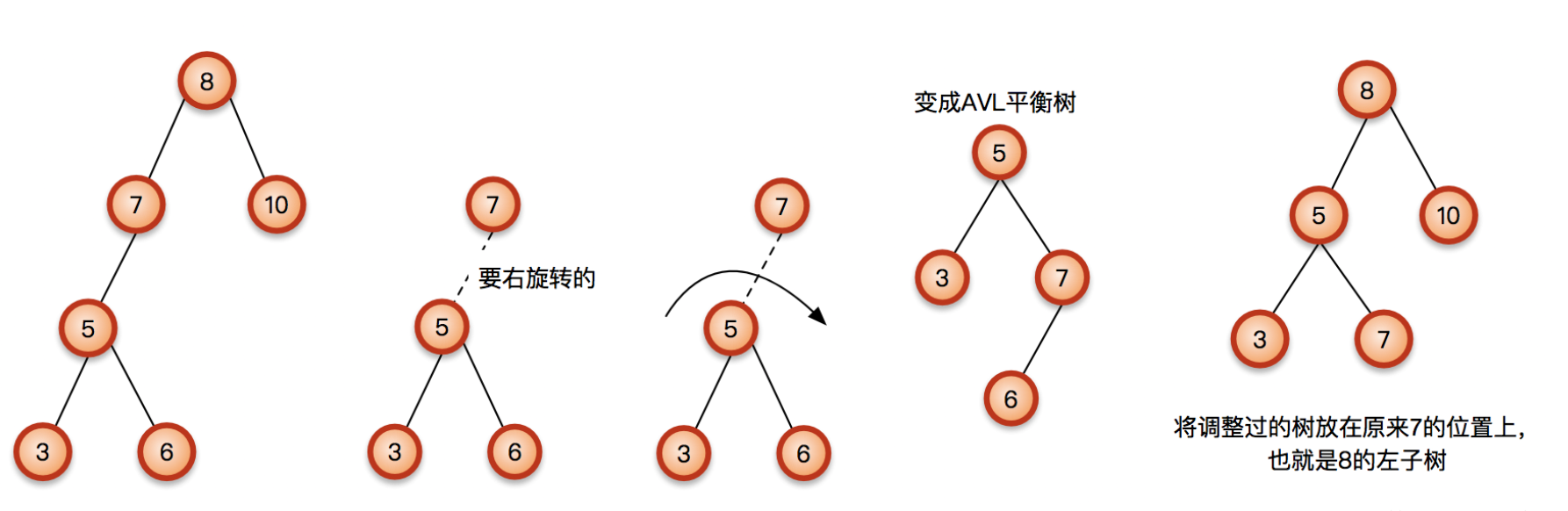
image.png
1:左旋（zag）逆时针操作 (右子树>左子树)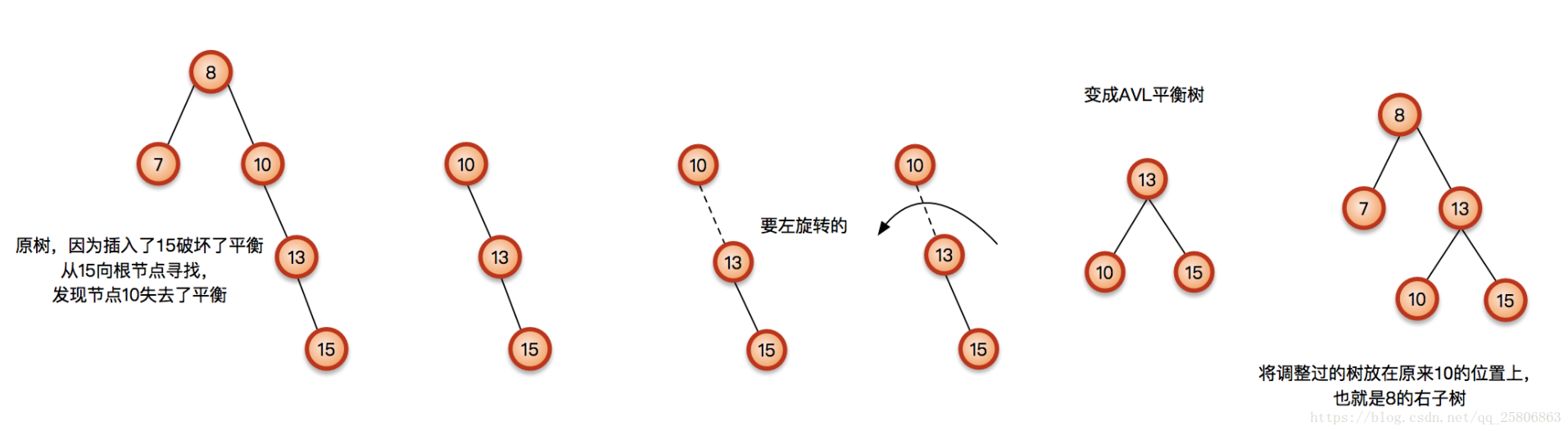
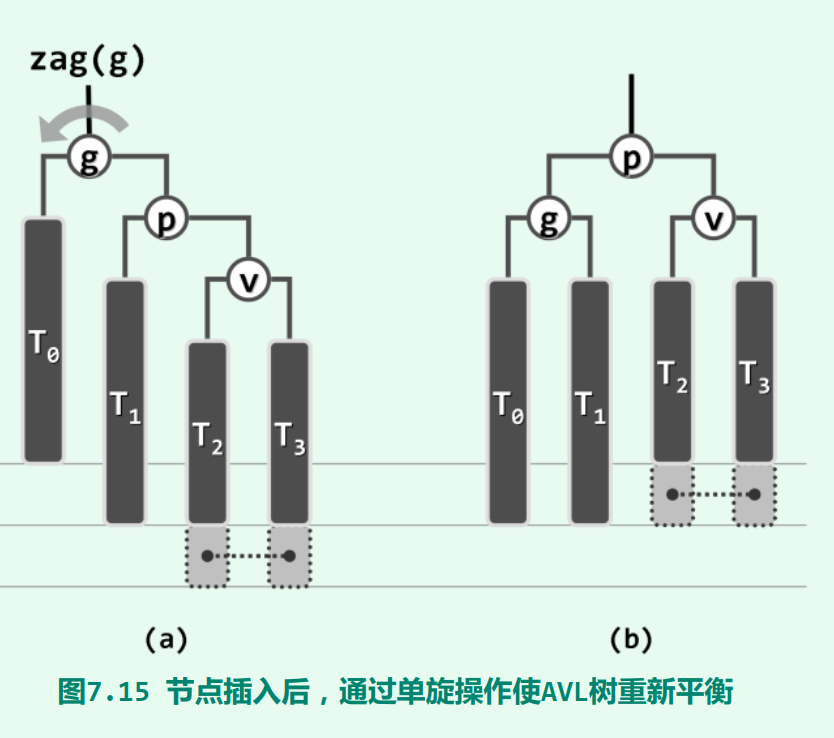
image.png
image.png
设v是p的右孩子，p是g的右孩子，只需要zag单旋就可以了（g是首次遇到的失衡祖先）

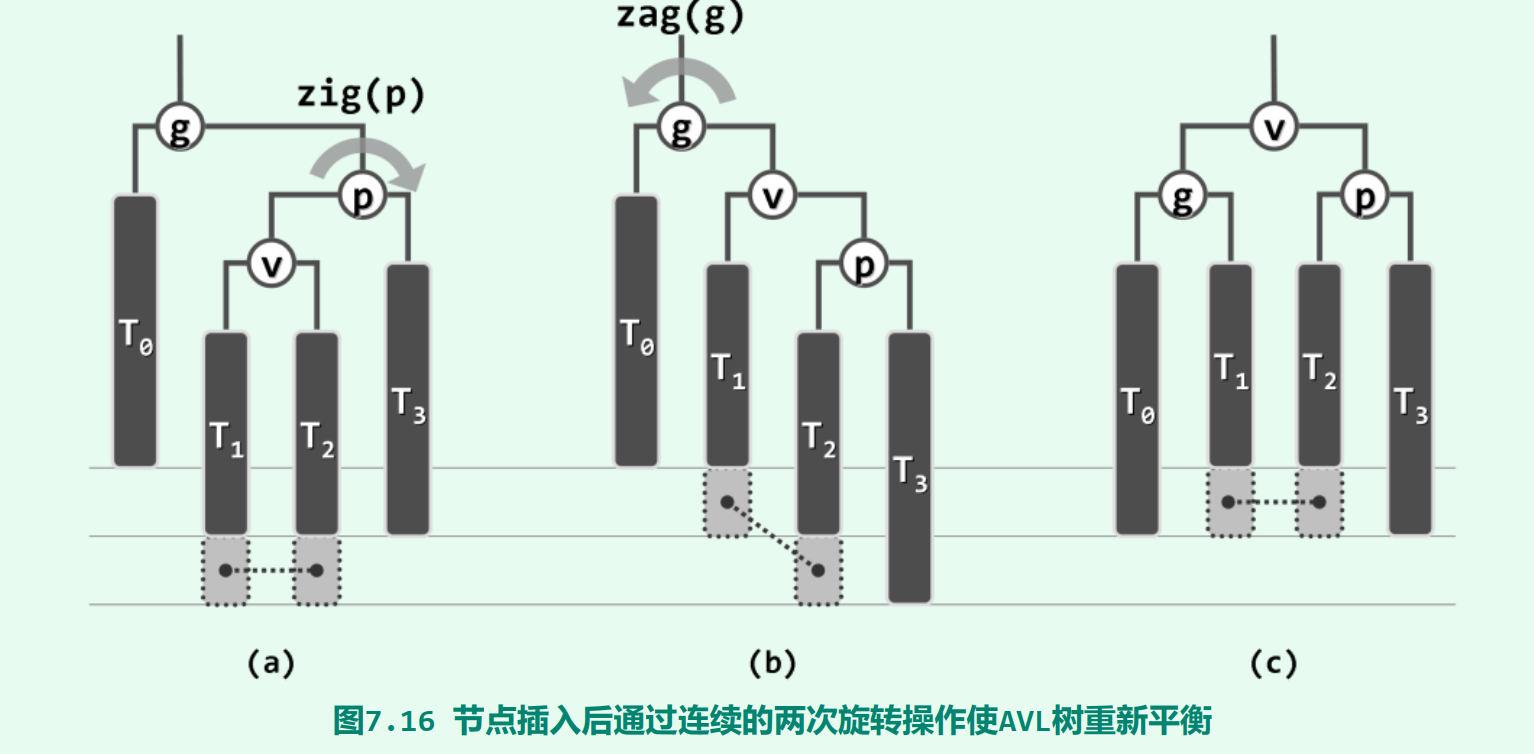
4.2.2 双旋

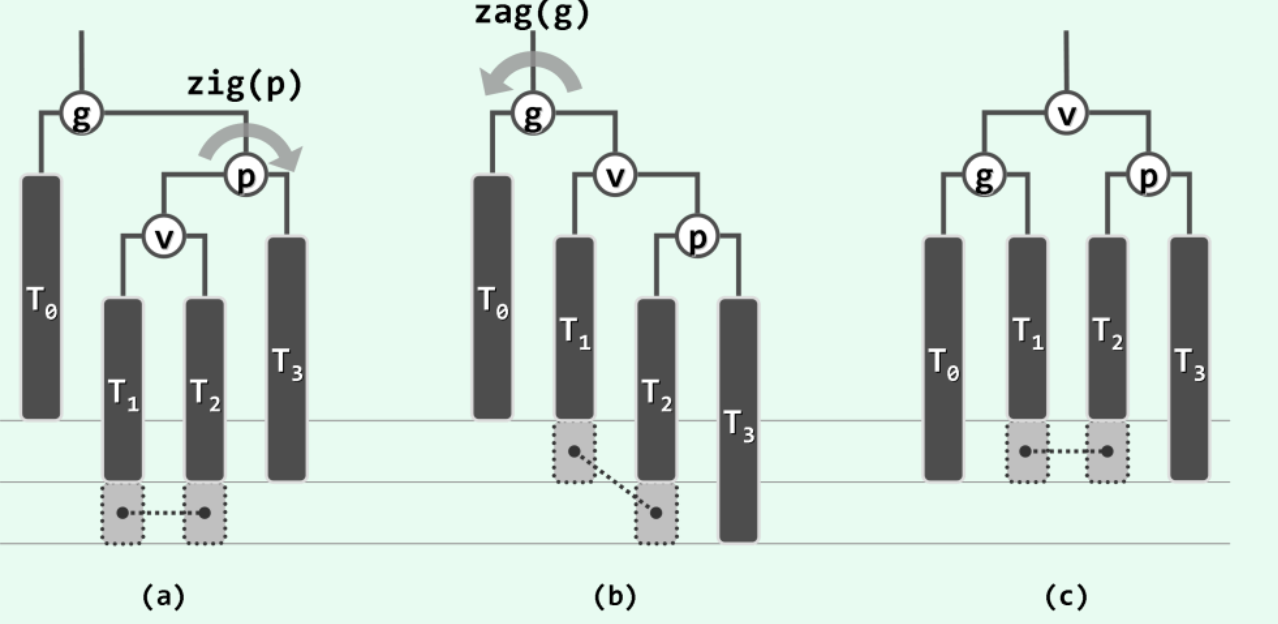
image.png
若p是g的左孩子，v是p的右孩子，就需要先右旋（p）然后左旋（g）。此类分别以父子节点为轴、方向互逆的持续两次旋转合称“双旋调整”。

4.3 节点删除

若删除后，首次遇到的失衡祖先g存在，则g的高度必与失衡前相同（参考节点删除算法）。

4.4 统一重平衡算法

无论对于插入或删除操作， 该算法也同样需要从刚发生修改的位置x出发逆行而上， 直至遇到最低的失衡节点g(x)。于是在g(x)更高一侧的子树内，其孩子节点p和孙子节点v必然存在，而且这一局部必然可以g(x)、 p和v为界，分解为四棵子树。