词典

1 跳转表

1.1 总体逻辑结构

内部由沿横向分层、沿纵向相互耦合的多个列表组成。每一水平列表称作一层（level） ，其中S0和Sh分别称作底层（bottom） 和顶层（top）。与通常的列表一样，同层节点之间可定义前驱与后继关系。为便于查找， 同层节点都按关键码排序，每层列表都设有头、尾哨兵节点。层次不同的节点可能沿纵向组成塔（tower），同一塔内的节点以高度为序也可定义前驱与后继关系。塔与词典中的词条一一对应。跳转表内各节点沿水平和垂直方向都可定义前驱和后继。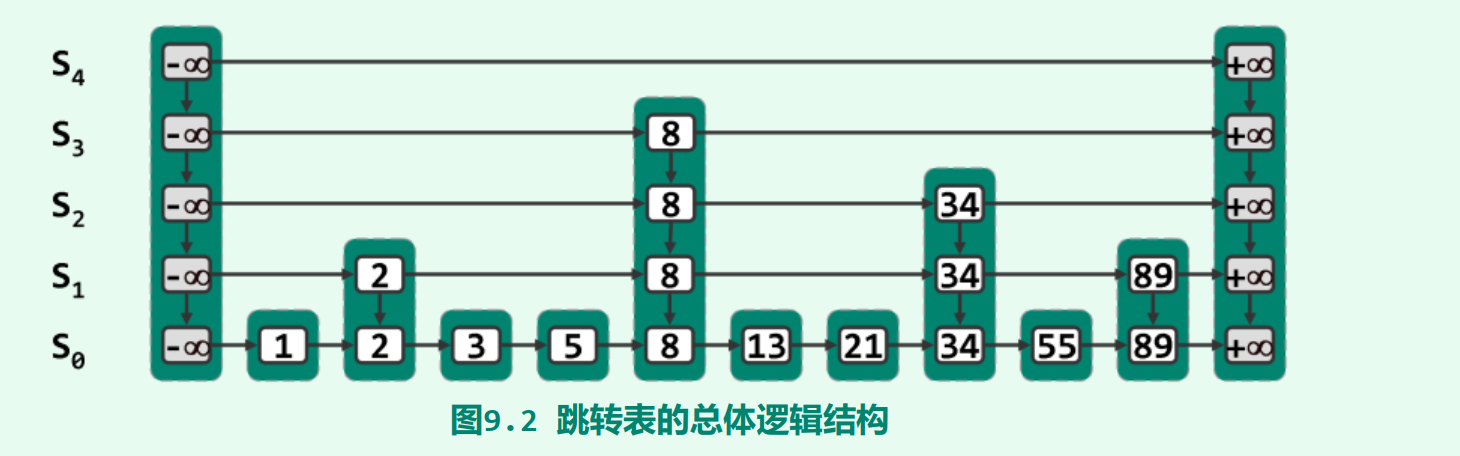

2 散列

此类方法以最基本的向量作为底层支撑结构，通过适当的散列函数在词条的关键码与向量单元的秩之间建立起映射关系。

2.1 兼顾空间利用率与速度

尽管词典中实际需要保存的词条数N（比如25000门）远远少于可能出现的词条数R（10^8门），但R个词条中的任何一个都有可能出现在词典中。即装填因子过小，导致空间利用率降低。

2.2 散列函数

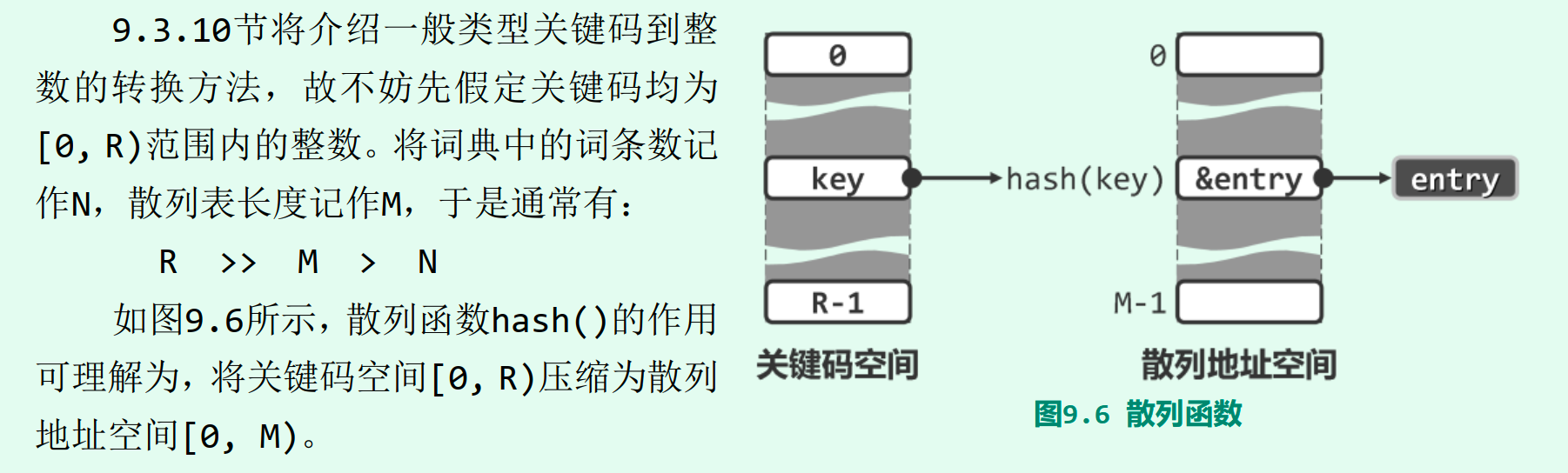
所有关键码经映射后应尽量覆盖整个地址空间[0, M)，唯此方可充分利用有限的散列表空间。
当然， 因定义域规模R远远大于取值域规模M， hash()不可能是单射。这就意味着，关键码不同的词条被映射到同一散列地址的情况称作散列冲突（collision） 难以彻底避免
在此，最为重要的一条原则就是，关键码映射到各桶的概率应尽量接近于1/M

2.2.1 除余法

一种最简单的映射办法，就是将散列表长度M取作为素数，并将关键码key映射至key关于M整除的余数

2.2.2 MAD法

除余法的缺陷：比如， 相邻关键码所对应的散列地址，总是彼此相邻；极小的关键码， 通常都被集中映射到散列表的起始区段。其中特别地， 0值居然是一个“不动点”，其散列地址总是0，而与散列表长度无关。

2.3 冲突及其排解

2.3.1 多槽位法

最直截了当的一种对策是，将彼此冲突的每一组词条组织为一个小规模的子词典，分别存放于它们共同对应的桶单元中。比如一种简便的方法是，统一将各桶细分为更小的称作槽位（slot）的若干单元，每一组槽位可组织为向量或列表。

2.3.2 独立链法

冲突排解的另一策略与多槽位（multiple slots）法类似，也令相互冲突的每组词条构成小规模的子词典， 只不过采用列表（而非向量）来实现各子词典