图

1. 概述

相互之间均可能存在二元关系的一组对象，从数据结构的角度分类，属于非线性结构（non-linear structure） 。 此类一般性的二元关系，属于图论（Graph Theory）的研究范畴。从算法的角度对此类结构的处理策略，是通过遍历将其转化为半线性结构，进而借助树结构已有的处理方法和技巧， 最终解决问题。

1.1 图

G = (V,E)
集合V中的元素称作顶点（vertex）； 集合E中的元素分别对应于V中的某一对顶点(u, v)，表示它们之间存在某种关系，称为边。
邻接关系：存在连边的任何两个点称为邻接关系。
关联关系：参与定义领接关系的顶点于邻接关系的关系为关联关系。

1.2 无向图、有向图及混合图。

若边(u, v)所对应顶点u和v的次序无所谓，则称作无向边，例如表示同学关系的边。反之若u和v不对等，则称(u, v)为有向边， 例如描述企业与银行之间的借贷关系，或者程序之间的相互调用关系的边。
无向边(u, v)也可记作(v, u)，而有向的(u, v)和(v, u)则不可混淆。这里约定，有向边(u, v)从u指向v，其中u称作该边的起点或尾顶点，而v称作该边的终点 或头顶点。
若E中各边均无方向，则G称作为无向图；若E只含有向边，则G为有向图。
相对而言，有向图的通用性更强，因为无向图和混合图都可转化为有向图。
连通分量：图中从一个顶点到达另一顶点，若存在至少一条路径，则称这两个顶点是连通着的。在无向图中，如果从顶点vi到顶点vj有路径，则称vi和vj连通。如果图中任意两个顶点之间都连通，则称该图为连通图，否则，将其中的较大连通子图称为连通分量。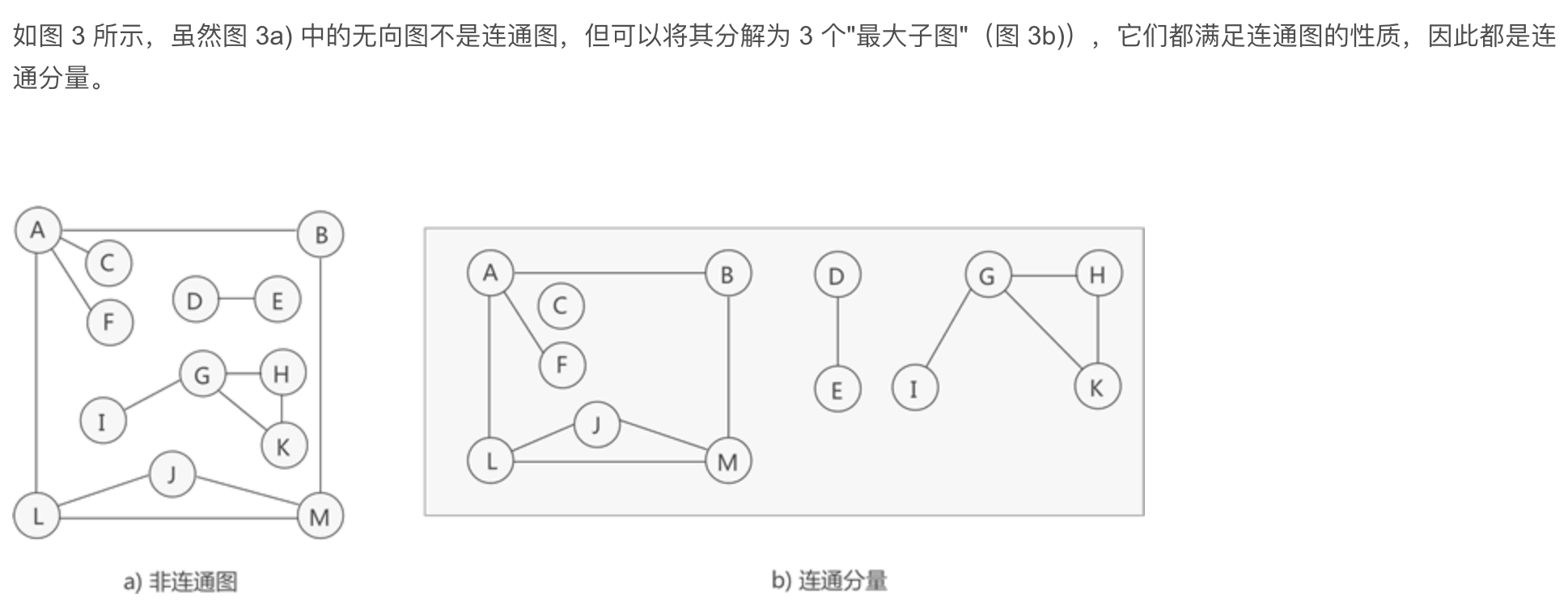

1.3 度

对于任何边e = (u, v)，称顶点u和v彼此邻接，互为邻居；而它们都与边e彼此关联。在无向图中，与顶点v关联的边数，称作v的度数记作deg(v)。
对于有向边e = (u, v)， e称作u的出边、 v的入边。v的出边总数称作其出度，入边总数称作其入度。

1.4 简单图

联接于同一顶点之间的边，称作自环。不含任何自环的图称作简单图。

1.5 通路与环路

通路边必须互异，但顶点却可能重复。
沿途顶点互异的通路，称作简单通路。
对于长度大于等于1的通路，若起止顶点相同，则称作环路。若沿途除起止点外所有顶点均互异， 则称作简单环路。不含任何环路的有向图，称作有向无环图。
特别地， 经过图中各边一次且恰好一次的环路 ，称作欧拉环路。
经过图中各顶点一次且恰好一次的环路，称作哈密尔顿环路。

1.6 带权网络

需通过一个权值函数来表达每条边e的额外信息， 为每一边e指定一个权重比如wt(e)即为边e的权重。各边均带有权重的图，称作带权图或带权网络，有时也简称网络（network），记作G(V, E, wt())。

1.7 复杂度

对于无向图，每一对顶点至多贡献一条边， 故总共不超过n(n - 1)/2条边。对于有向图，每一对顶点都可能贡献（互逆的）两条边，因此至多可有n(n - 1)条边。

2. 邻接矩阵

3. 邻接表

4. 图遍历算法概述

图的遍历不仅需要访问所有顶点一次且仅一次；此外，图遍历同时还需要访问所有的边一次且仅一次。
图中顶点之间可能存在多条通路， 故为避免对顶点的重复访问， 在遍历的过程中， 通常还要动态地设置各顶点不同的状态， 并随着遍历的进程不断地转换状态，直至最后的“访问完毕” 。图的遍历更加强调对处于特定状态顶点的甄别与查找，故也称作图搜索。
各种图搜索之间的区别，体现为边分类结果的不同，以及所得遍历树（ 森林） 的结构差异。其决定因素在于， 搜索过程中的每一步迭代，将依照何种策略来选取下一接受访问的顶点。实质的差异应体现在， 当有多个顶点已被访问到，应该优先从谁的邻居中选取下一顶点。
图的遍历的本质是完成非线性结构到线性结构的转换，也就是将任何一幅图转化为对应的树，或者严格的讲是支撑树。

5. 广度优先搜索(breadth-first search BFC)

越早被访问到的顶点，其邻居越优先被调用。
在所有已访问到的顶点中，仍有邻居尚未访问者，构成前沿集。
反复从前沿集中找到最早被访问到的顶点v， 若其邻居均已访问到，则将其逐出前沿集；否则，随意选出一个顶点v尚未访问到的邻居，并将其加入到前沿集中。
效果等同于层次遍历，前沿集内顶点的深度始终相差不超过一。

深度优先搜索(depth-first search DFS)

优先选取最后一个被访问到的顶点的邻居
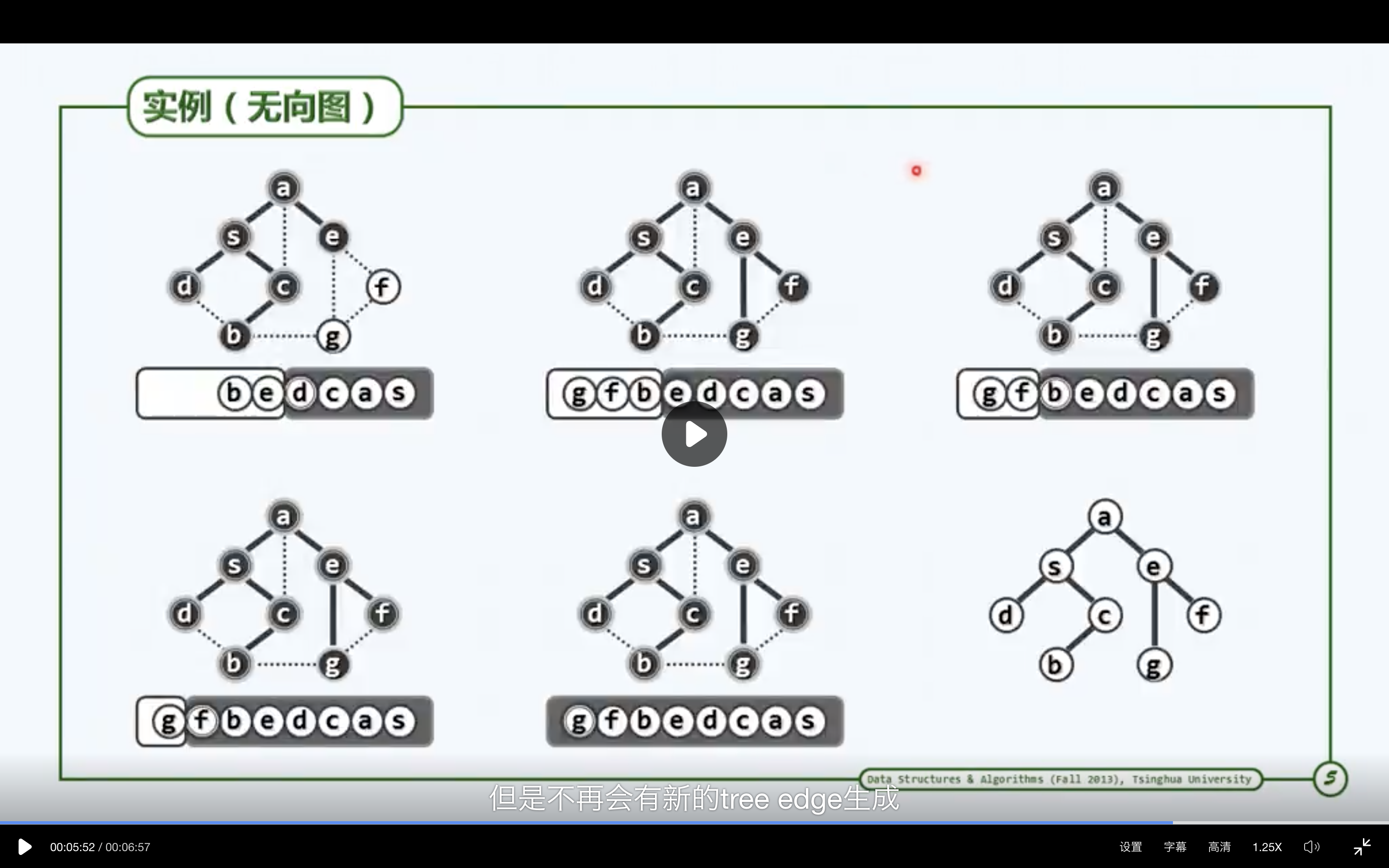
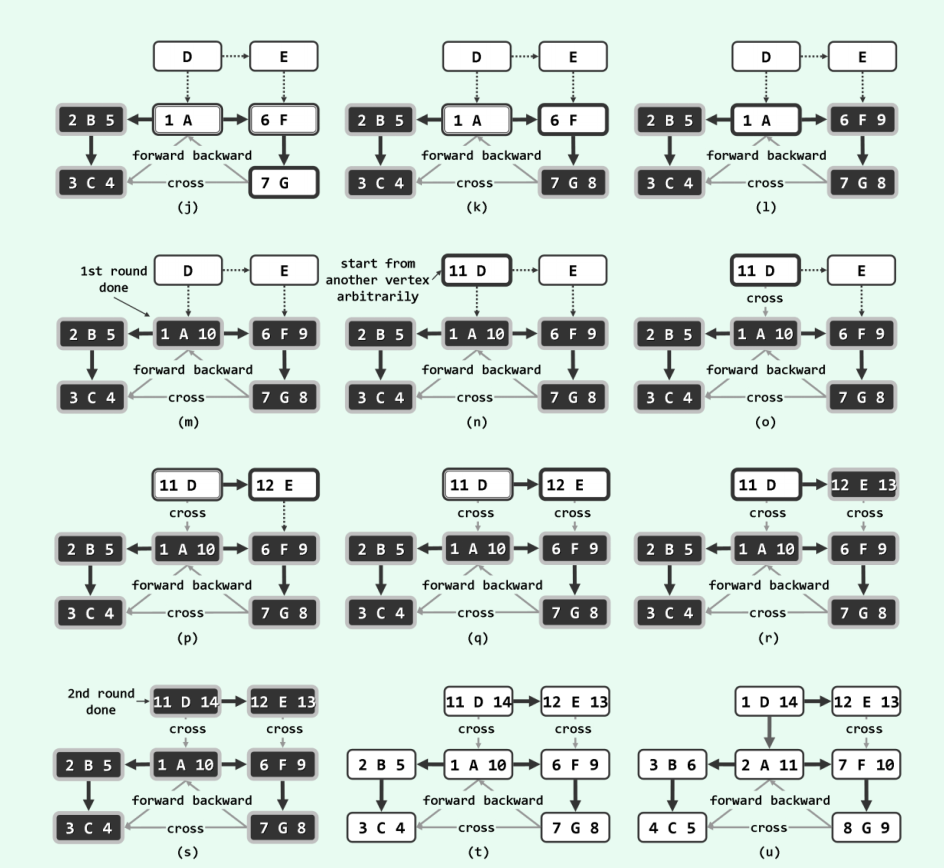
以顶点s为基点的DFS搜索，将首先访问顶点s；再从s所有尚未访问到的邻居中任取其一， 并以之为基点， 递归地执行DFS搜索。各顶点被访问到的次序，类似于树的先序遍历。各顶点被访问完毕的次序，类似于树的后序遍历。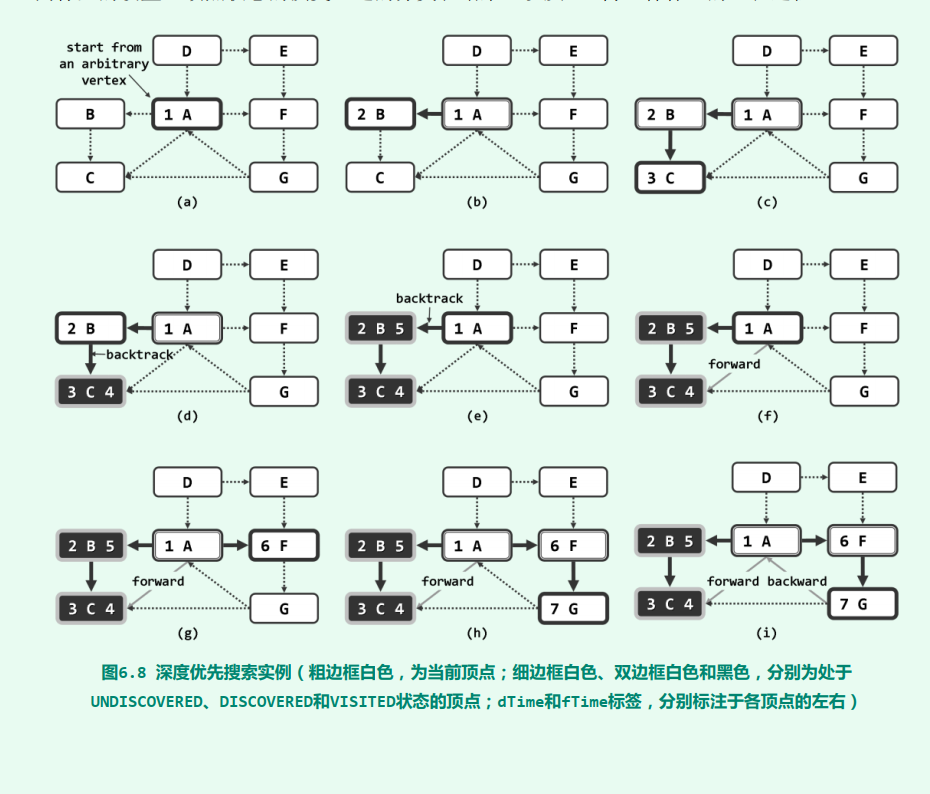

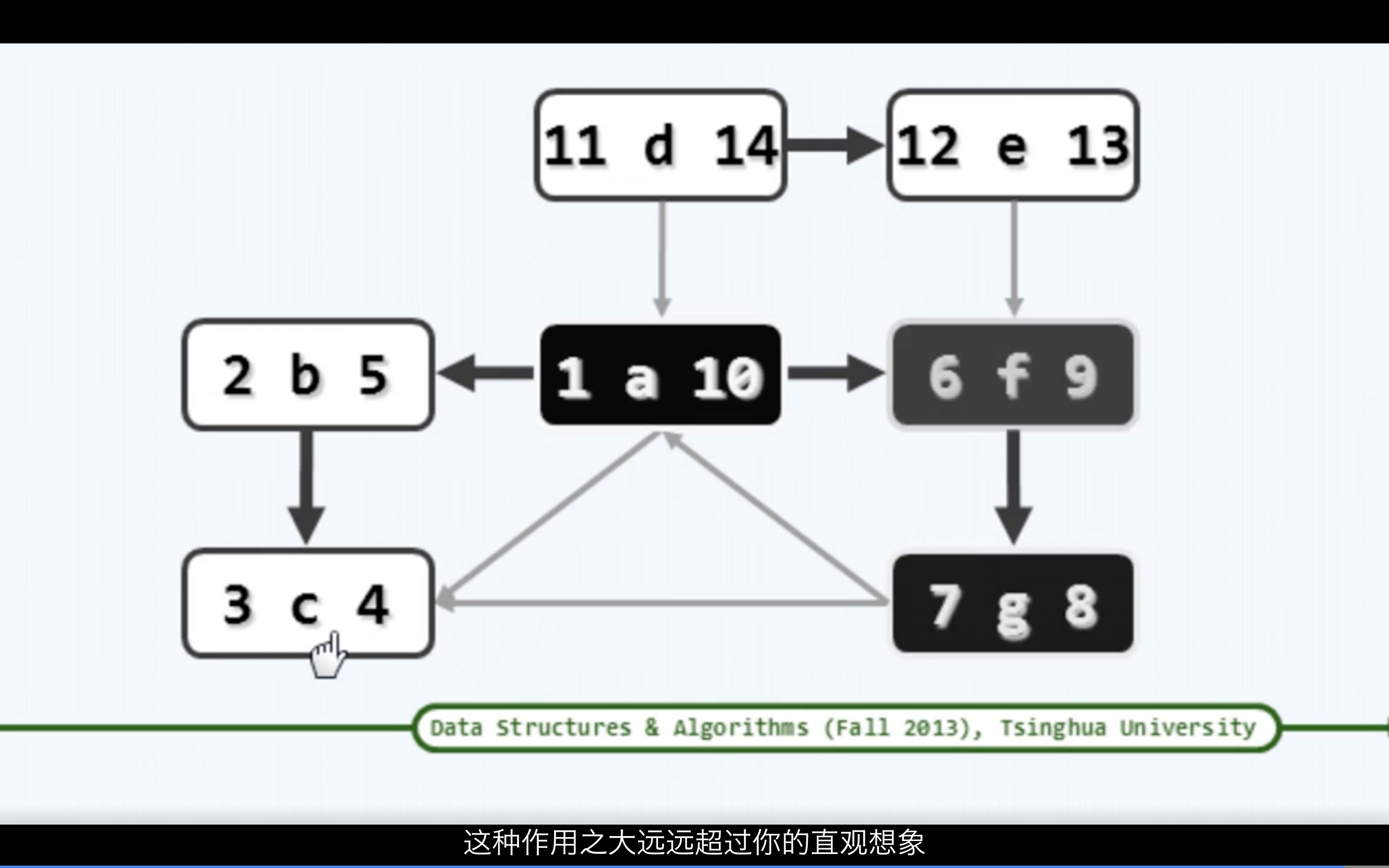
拓扑排序

给定某个实际应用的有向图，如何在与该图“相容”的前提下，将所有顶点排成一个线性序列。
“相容”的准确含义是：每一个顶点都不会通过边，指向其在此序列中的前驱顶点。这样的一个线性序列称为原有向图的一个拓扑排序。
实际上， 在任一有限偏序集中， 必有极值元素（尽管未必唯一）； 相应地， 任一有向无环图，也必包含入度为零的顶点。否则，每个顶点都至少有一条入边， 这意味着图中包含环路。
有向无环图(DAG)的拓扑排序必然存在。任一有向无环图，也必然包含入度为零的顶点。于是，只要将入度为0的顶点m（及其关联边） 从图G中取出， 则剩余的G’依然是有向无环图，故其拓扑排序也必然存在。
极大元素：入度为零的顶点
极小元素： 该元素作为顶点，出度为零的顶点；在对有向无环图的DFS搜索中，首先因访问完成而转换至VISITED状态的顶点m， 也必然具有这一性质。
DFS搜索过程中各顶点被标记为VISITED的次序，恰好（按逆序）给出了原图的一个拓扑排序。

双连通域分解

关节点与双连通域

关节点：无向图G，若删除顶点v后G所包含的连通域增多，则v称作切割节点或关节点。
双连通图：不含任何关节点的图称为双连通图。任一无向图都可视作由若干个极大的双连通子图组合而成，这样每一个子图都称作原图的一个双连通域。

优先级搜索

BFS、DFS每一种选取策略都等效于， 给所有顶点赋予不同的优先级， 而且随着算法的推进不断调整；而每一步迭代所选取的顶点， 都是当时的优先级最高者。

最小支撑树

支撑树

无环连通子图

连通图G的某一无环连通子图T若覆盖G中所有的顶点，则称作G的一棵支撑树或生成树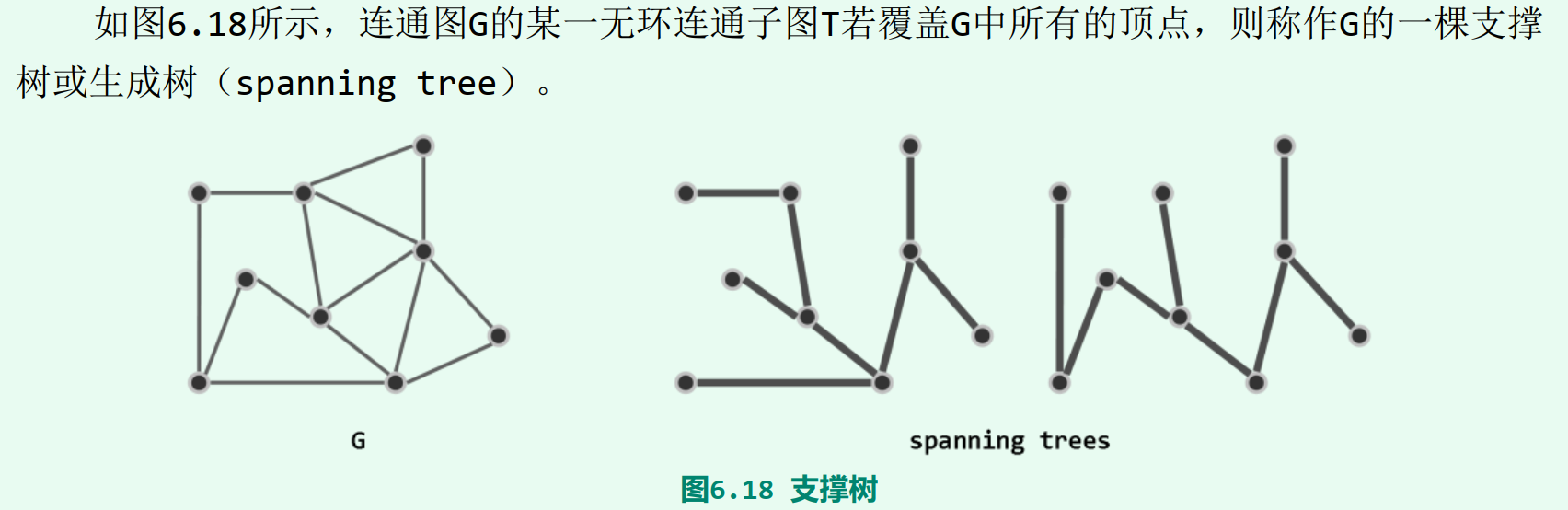

就保留原图中边的数目而言，支撑树既是“禁止环路”前提下的极大子图，也是“保持连通”前提下的最小子图。

最小支撑树

若图G为一带权网络，则每一棵支撑树的成本（cost） 即为其所采用各边权重的总和。在G的所有支撑树中，成本最低者称作最小支撑树(MST)

歧义性

尽管同一带权网络通常都有多棵支撑树，但总数毕竟有限， 故必有最低的总体成本。 然而，总体成本最低的支撑树却未必唯一。(若每条边的权重相同)。可以通过附加某种次序即可消除这种歧义性。

Prim算法

割与极短跨越边

图G = (V; E)中，顶点集V的任一非平凡子集U及其补集V\U都构成G的一个割（cut） ，记作(U : V\U)。若边uv满足u属于U且v不属于U，则称作该割的一条跨越边（crossing edge）
Prim算法的正确性基于以下事实：最小支撑树总是会采用联接每一割的最短跨越边

最短路径

最短路径树

单调性

歧义性

无环性