比较器

当然，除了与无序向量一样需要支持元素之间的“判等” 操作，有序向量的定义中实际上还
隐含了另一更强的先决条件：各元素之间必须能够比较大小。

有序性甄别

如果元素之间存在有序性，有序向量的查找、唯一化等操作可以更快的完成，顺序扫描整个向量，逐一比较每一对相邻元素。

唯一化

出于效率的考虑，为清除无序向量中的重复元素，一般做法往往是首先将其转化为有序向量
有序向量中的重复元素可批量删除

查找

有序向量S中的元素不再随机分布，秩r是S[r]在S中按大小的相对位次，位于S[r]前（后）
方的元素均不致于更大（小）。当所有元素互异时， r即是S中小于S[r]的元素数目。一般地，
若小于、等于S[r]的元素各有i、 k个，则该元素及其雷同元素应集中分布于S[i, i + k)
利用上述性质，有序向量的查找操作可以更加高效的完成。

二分查找（版本A）

减而治之

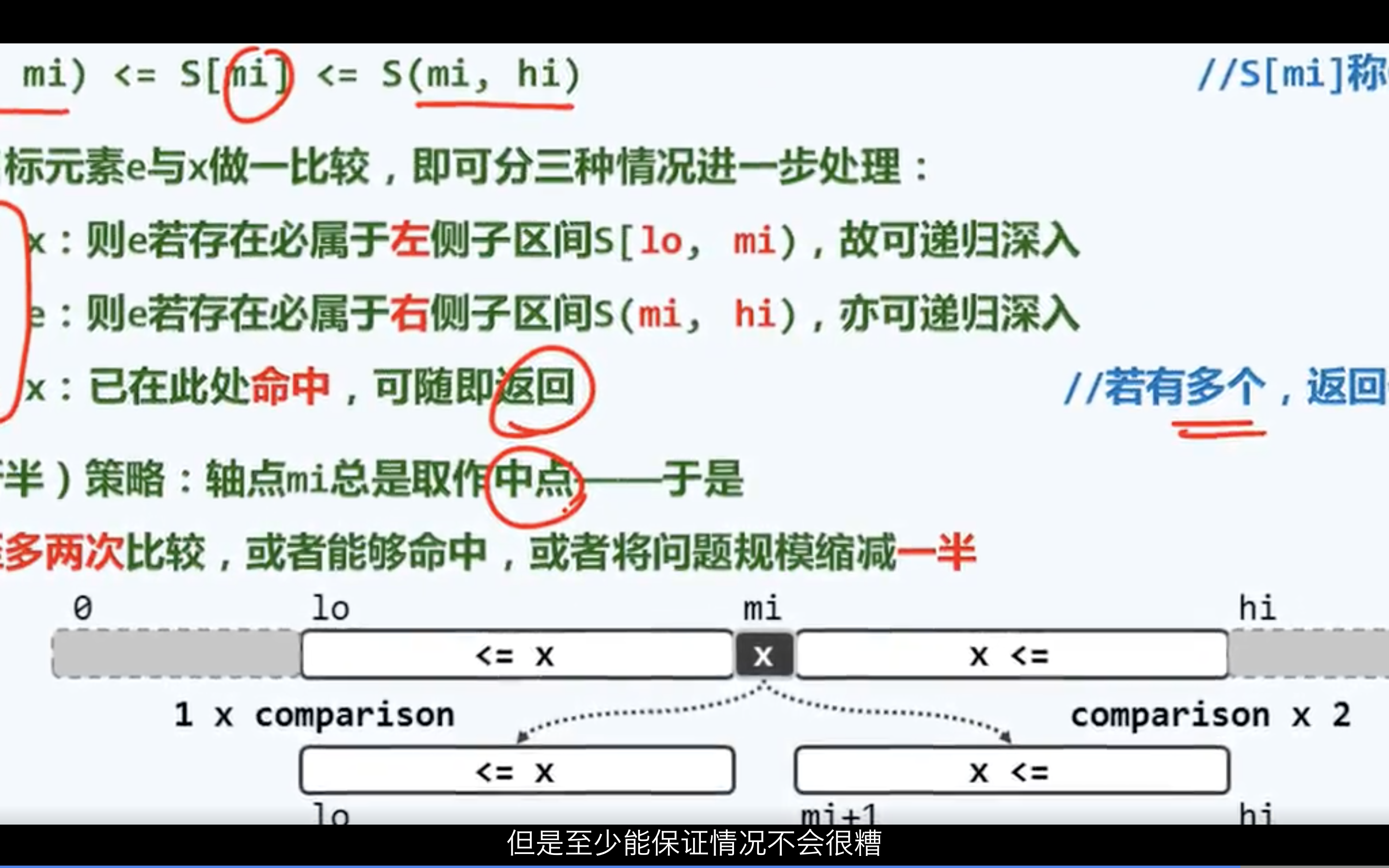
image.png

  1.     //二分查找
  2.     binSearch(arr, lo, hi) { 
  3.         while (lo < hi) {
  4.             const mid = (lo + hi) >> 1;
  5.             if (e < arr[mid]) {
  6.                 hi = mid
  7.             }else if (arr[mid] < e) {
  8.                 lo = mid+1
  9.             } else {
  10.                 return mid
  11.             }
  12.         }
  13.         return -1
  14.     }

复杂度

image.png

查找长度

以上迭代过程所涉及的计算， 主要分为两类： 元素的大小比较、秩的算术运算及其赋值。
查找算法的整体效率也更主要地取决于其中所执行的元素大小比较操作的次数，即所谓查找长度（search length）

成功、失败查找长度

image.png

不足

尽管二分查找算法（版本A） 即便在最坏情况下也可保证O(logn)的渐进时间复杂度，但就
其常系数1.5而言仍有改进余地。以成功查找为例，即便是迭代次数相同的情况， 对应的查找长
度也不尽相等。究其根源在于，在每一步迭代中为确定左、右分支方向，分别需要做1次或2次元
素比较， 从而造成不同情况所对应查找长度的不均衡。尽管该版本从表面上看完全均衡，但我们
通过以上细致的分析已经看出，最短和最长分支所对应的查找长度相差约两倍

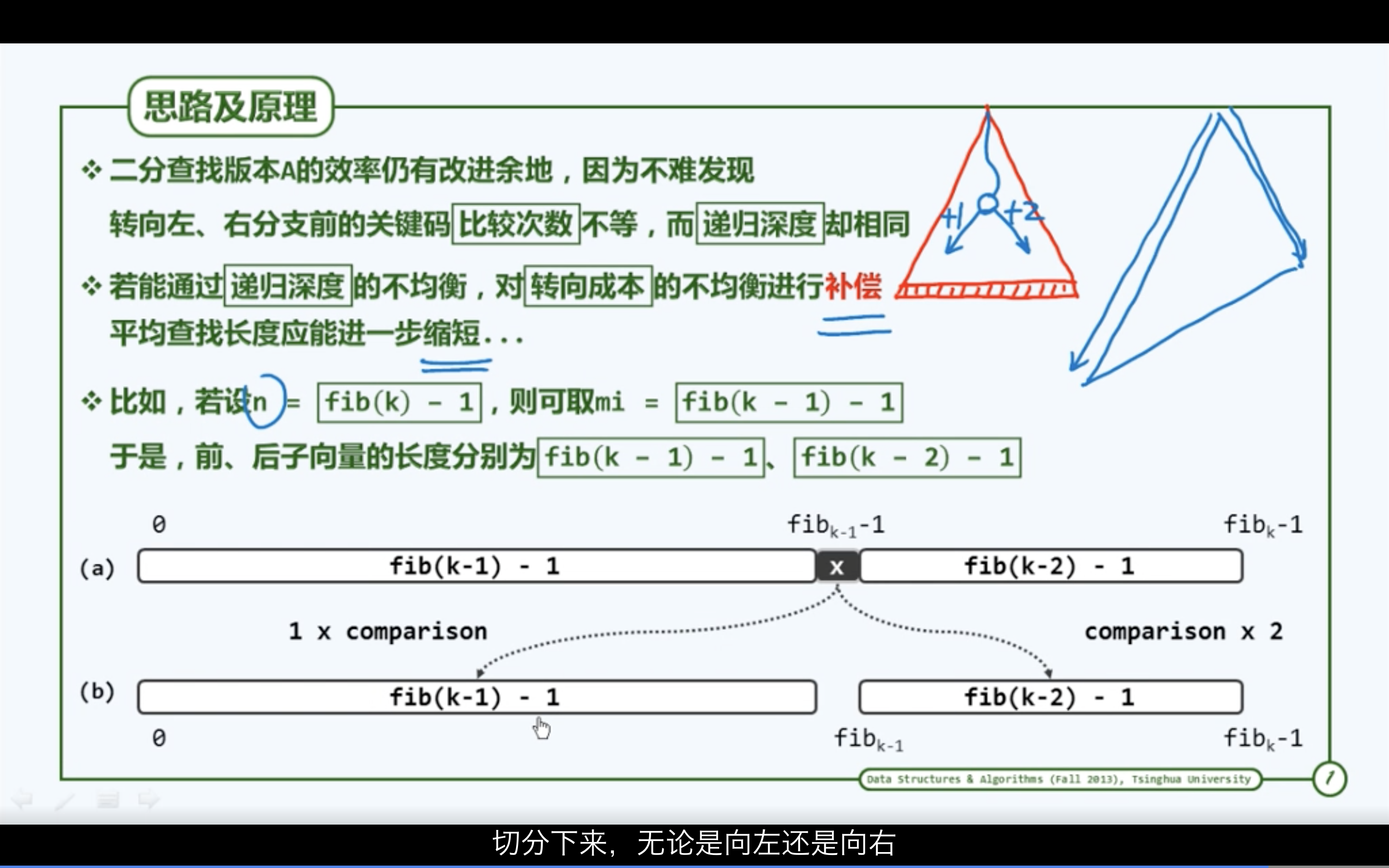
Fibonacci查找

更希望在左侧的转向多一些

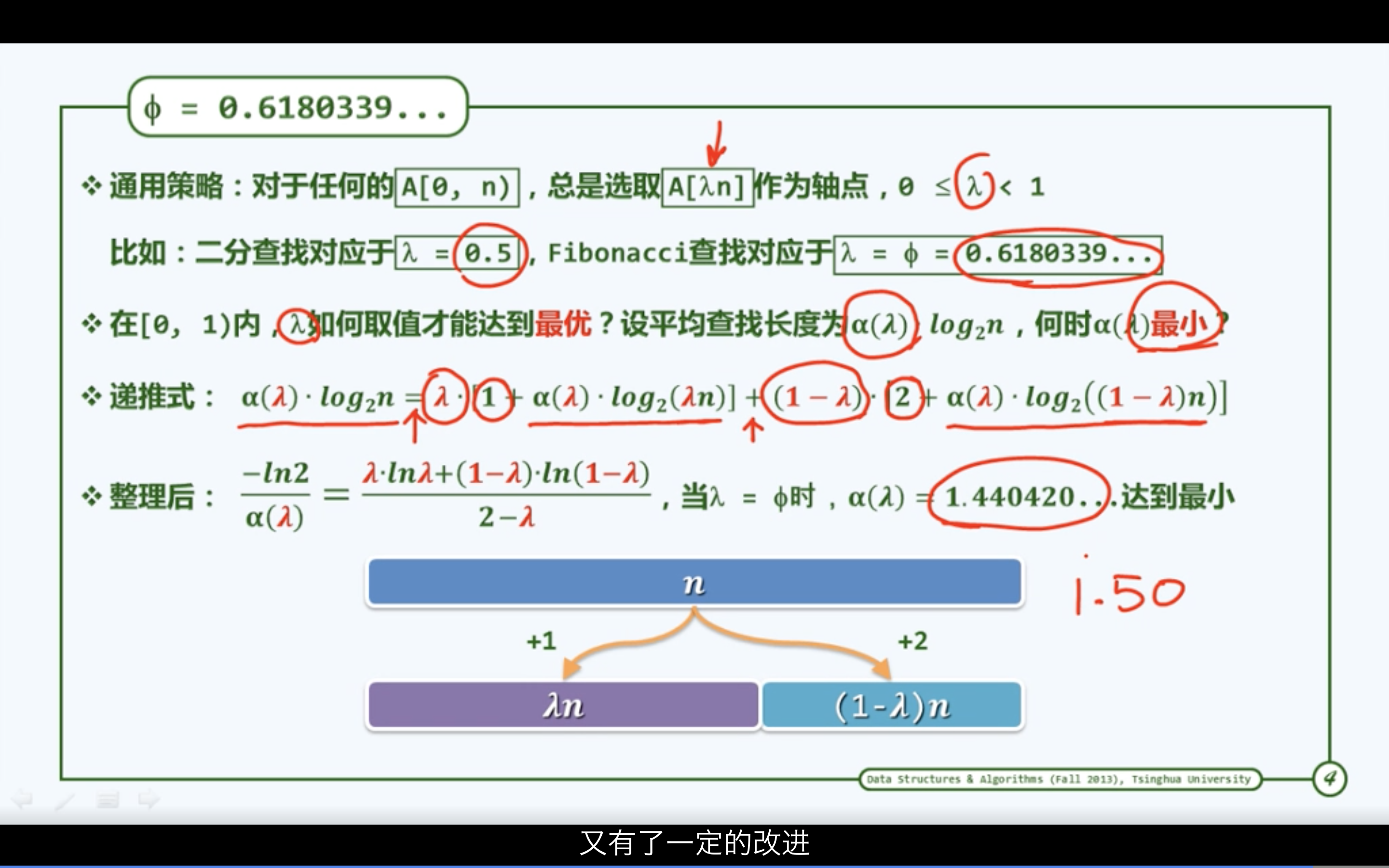
黄金分割

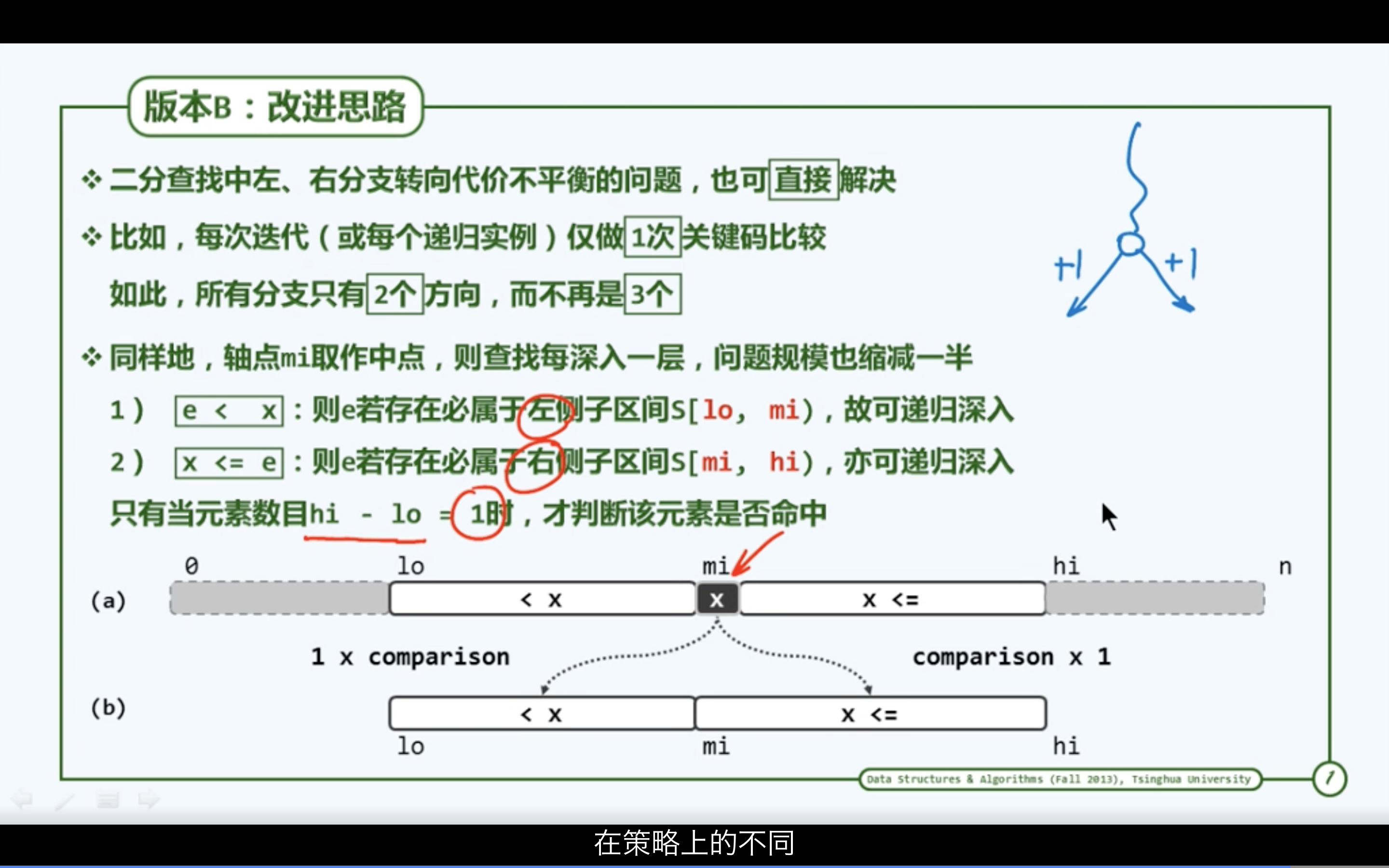
image.png

定量分析

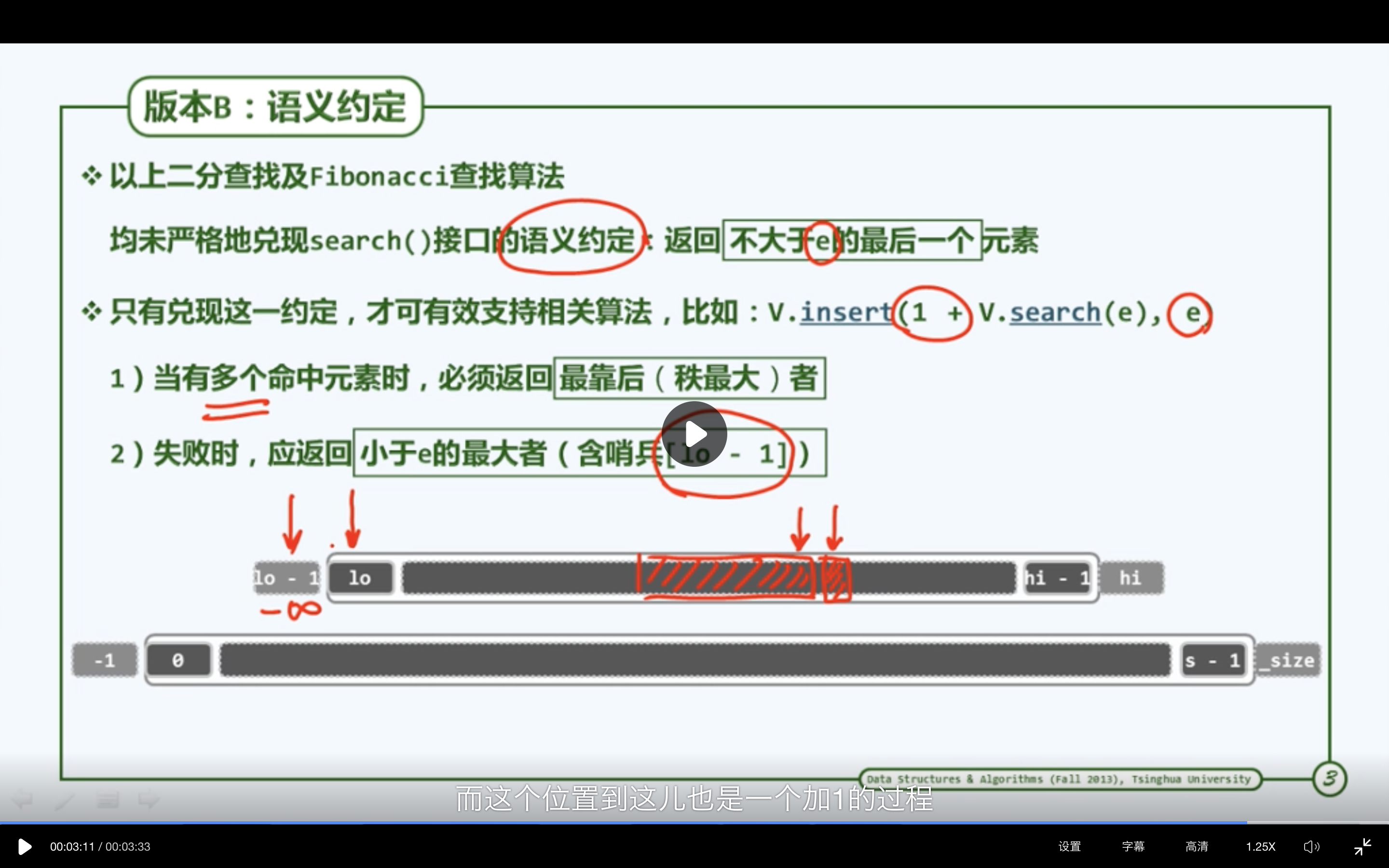
image.png

二分查找（版本B）

向左转向或向右转向所做的比较次数都相等，都强制为1。

改进思路

image.png

语义约定

image.png
只有等到区间的宽度已不足2个单元时迭代才会终止，最后再通过一次比对判断查找是否成功

  1.     //二分查找B
  2.     binSearchB(arr, e,lo, hi) { 
  3.         while (1<hi-lo) { //有效区间的宽度缩短为1时，算法才会终止
  4.             const mid = (lo + hi) >> 1; // 以中心为轴点，经比较后确定深入
  5.             e < arr[mid] ? (hi = mid) : (lo = mid) // [lo,mid) 或[mid,hi)
  6.         } //出口时hi = lo +1 查找区间仅含arr[lo]
  7.         return (e===arr[lo]) ? lo : -1
  8.     }

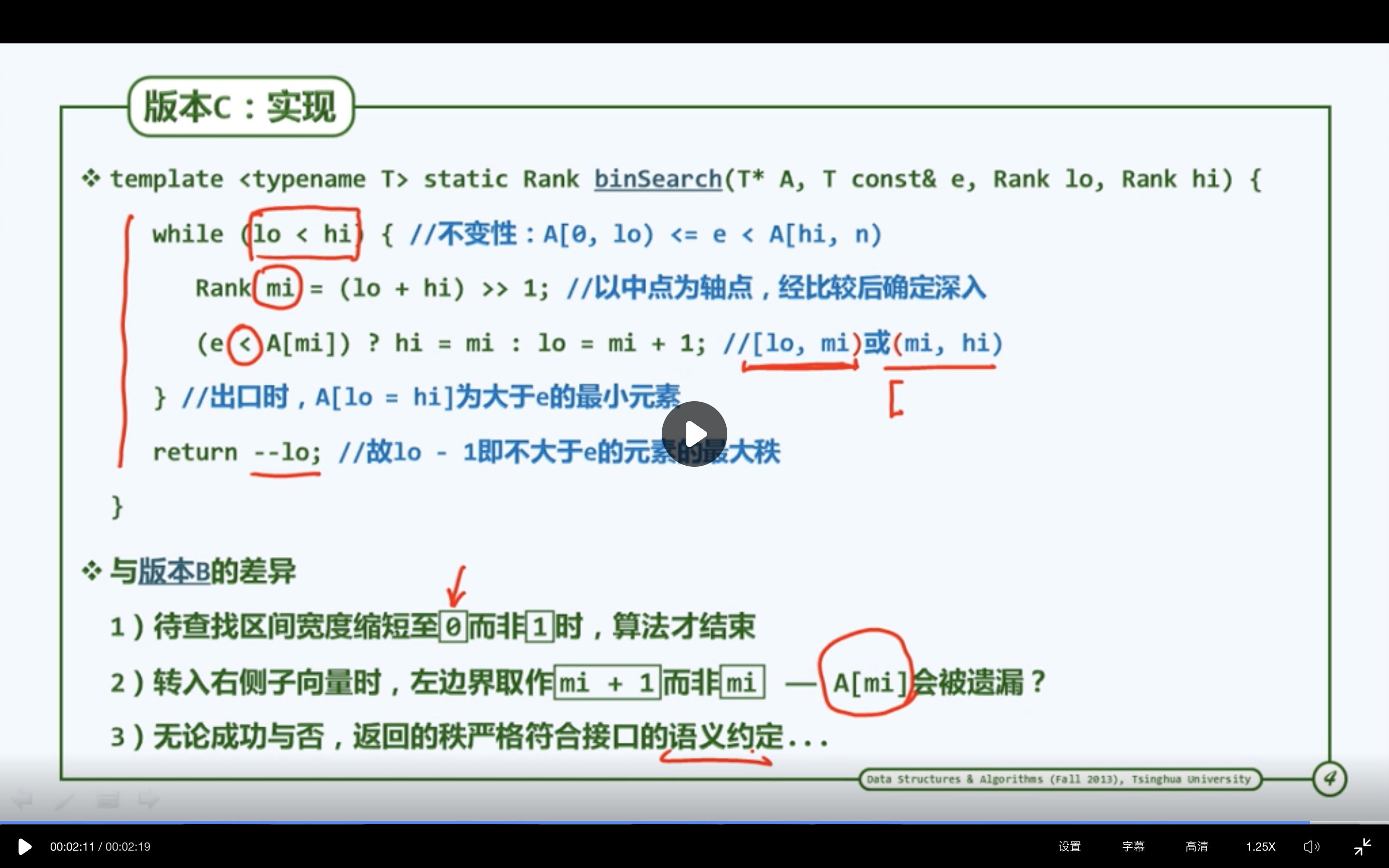
二分查找（版本C）

image.png