栈

栈的典型应用

逆序输出

栈数据结构比较适合以下典型问题：
首先，虽有明确的算法，但其解答却以线性序列的形式给出；其次，无论是递归还是迭代实现， 该序列都是依逆序计算输出的；最后，输入和输出规模不确定，难以事先确定盛放输出数据的容器大小。

递归嵌套

栈混洗

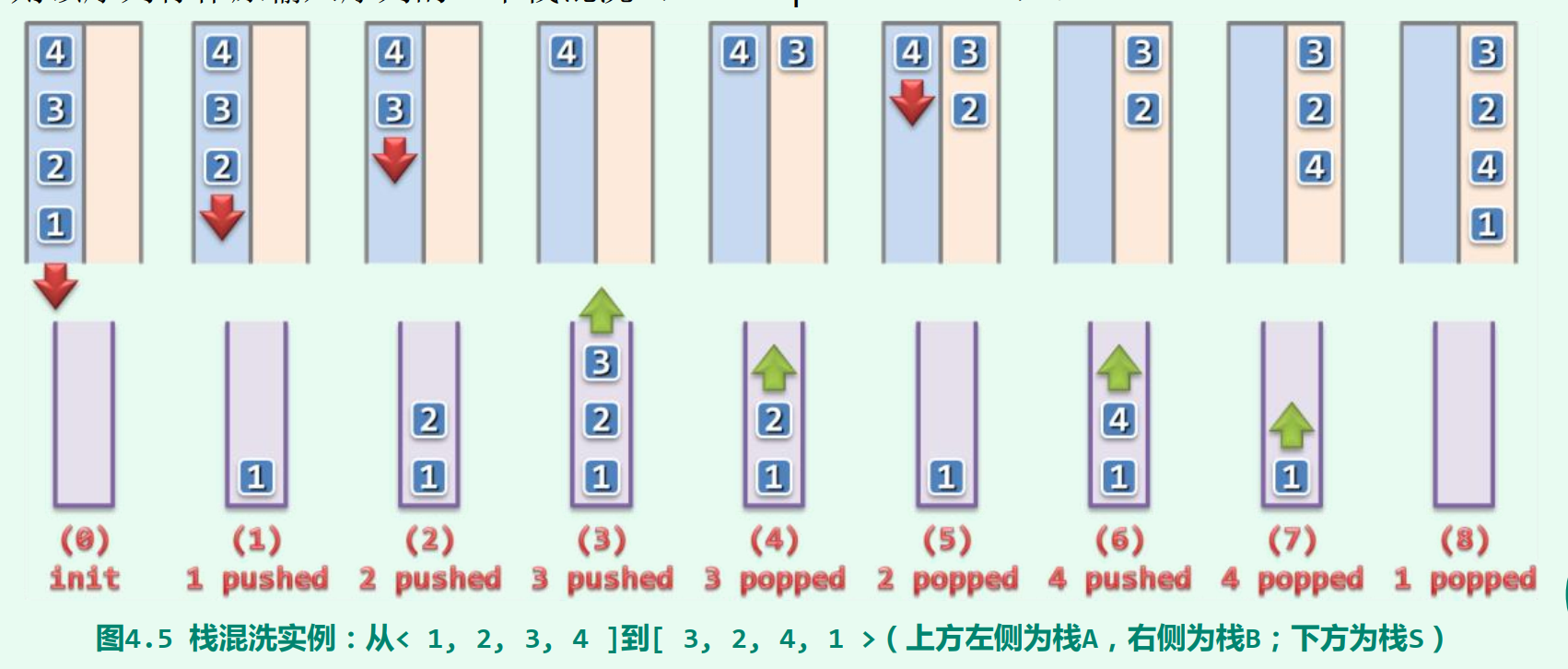
每一栈混洗都对应于由栈S的n次push操作和pop操作构成的某一合法序列。反之， 由n次push和n次pop构成的任何操作序列，只要满足“任一前缀中的push不少于pop” 这一限制，则该序列也必然对应于某个栈混洗。

延迟缓冲

一些应用问题中，输入可分解为多个单元并通过迭代依次扫描处理，但过程中的各步计算往往滞后于扫描的进度，需要待到必要的信息已完整到一定程度之后， 才能作出判断并实施计算。在这类场合，栈结构则可以扮演数据缓冲区的角色。

逆波兰表达式

试探回溯法

试探与回溯

事实上，很多应用问题的解，在形式上都可看作若干元素按特定次序构成的一个序列。旅行商问题，尽管此类问题本身的描述并不复杂，但遗憾的是，由于所涉及元素（比如城市）的每一排列都是一个候选解，它们往往构成一个极大的搜索空间。通常，其搜索空间的规模与全排列总数大体相当，为n!。
为此，必须基于对应用问题的深刻理解，利用问题本身具有的某些规律尽可能多、尽可能早地排除搜索空间中的候选解。其中一种重要的技巧就是，根据候选解的某些局部特征，以候选解子集为单位批量地排除。这一技巧也称为剪枝。
与之对应的算法多呈现为如下模式。从零开始，尝试逐步增加候选解的长度。更准确地，这一过程是在成批地
考查具有特定前缀的所有候选解。这种从长度上逐步向目标解靠近的尝试，称作试探（ probing） 。作为解的局部特征，特征前缀在试探的过程中一旦被发现与目标解不合，则收缩到此前一步的长度，然后继续试探下一可能的组合。特征前缀长度缩减的这类操纵，称作回溯（ backtracking）。
还需要保证搜索过的部分不被重复搜索，办法之一就是，在剪枝的位置留下某种标记。同样地， 这类标记也需兑现为具体的数据结构。

八皇后

迷宫寻径