减而治之

image.png

版本A

  1.   const binSearchA = (elem,e,lo,hi) => {
  2.     while (lo < hi) {
  3.       const mi = (lo + hi) >> 1;
  4.       if (e < elem[mi]) {
  5.         hi = mi; //[lo,mi)
  6.       } else if (elem[mi] < e) {
  7.         lo = mi + 1; //(mi,hi)
  8.       } else {
  9.         return mi;
  10.       }
  11.     }
  12.     return -1;
  13.   };

不足之处

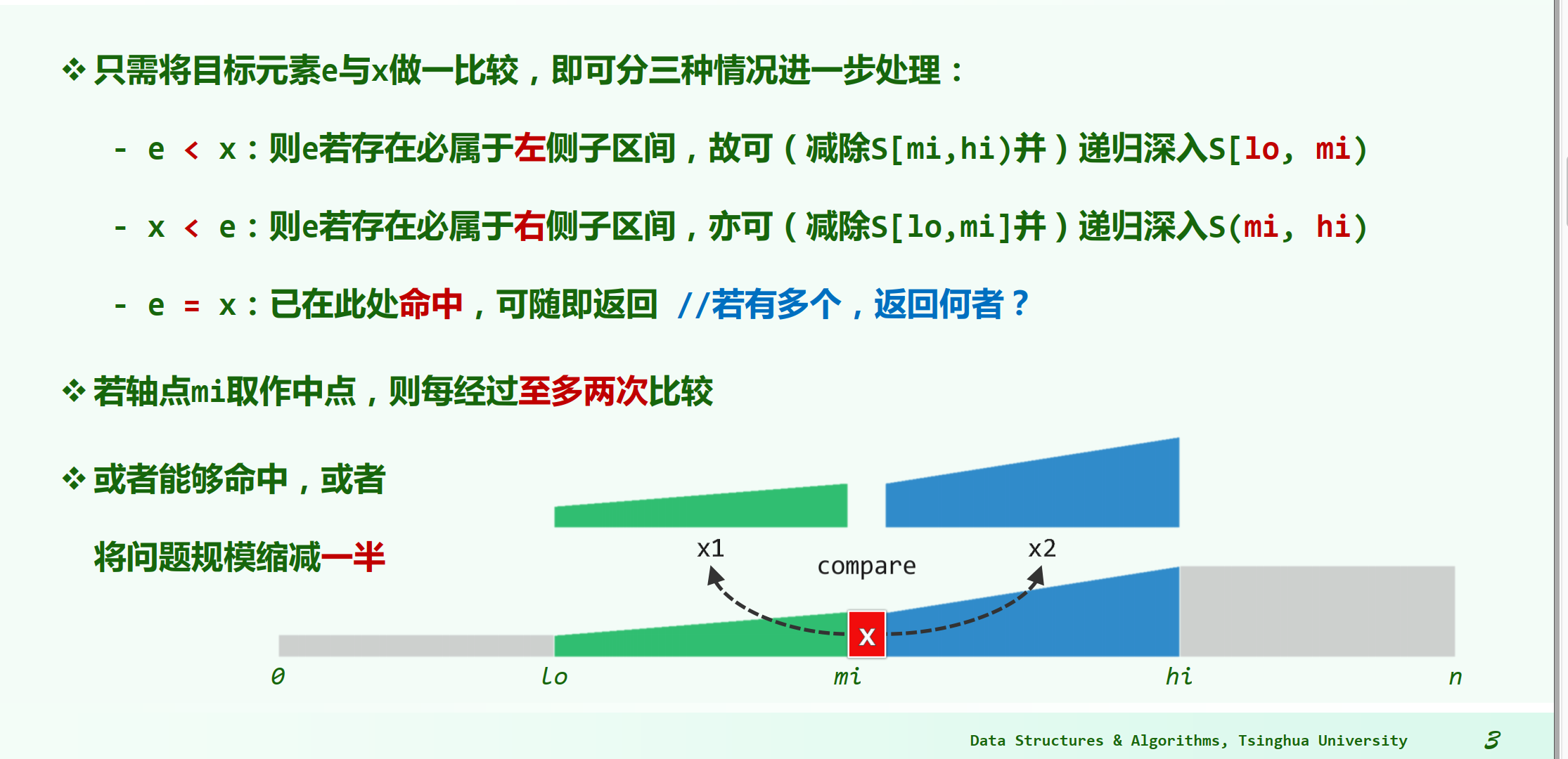
  1. 有多个命中元素时，不能保证返回秩最大者；查找失败时，简单地返回-1，而不能指示失败的位置。

  2. 在每一步迭代中为确定左、右分支方向，分别需要做1次或2次元素比较， 从而造成不同情况所对应查找长度的不均衡。

    版本B

    改进思路

    实际上还有另一更为直接的方法，即令以上两项的常系数同时等于1。也就是说，无论朝哪
    个方向深入，都只需做1次元素的大小比较。相应地，算法在每步迭代中（或递归层次上）都只
    有两个分支方向，而不再是三个。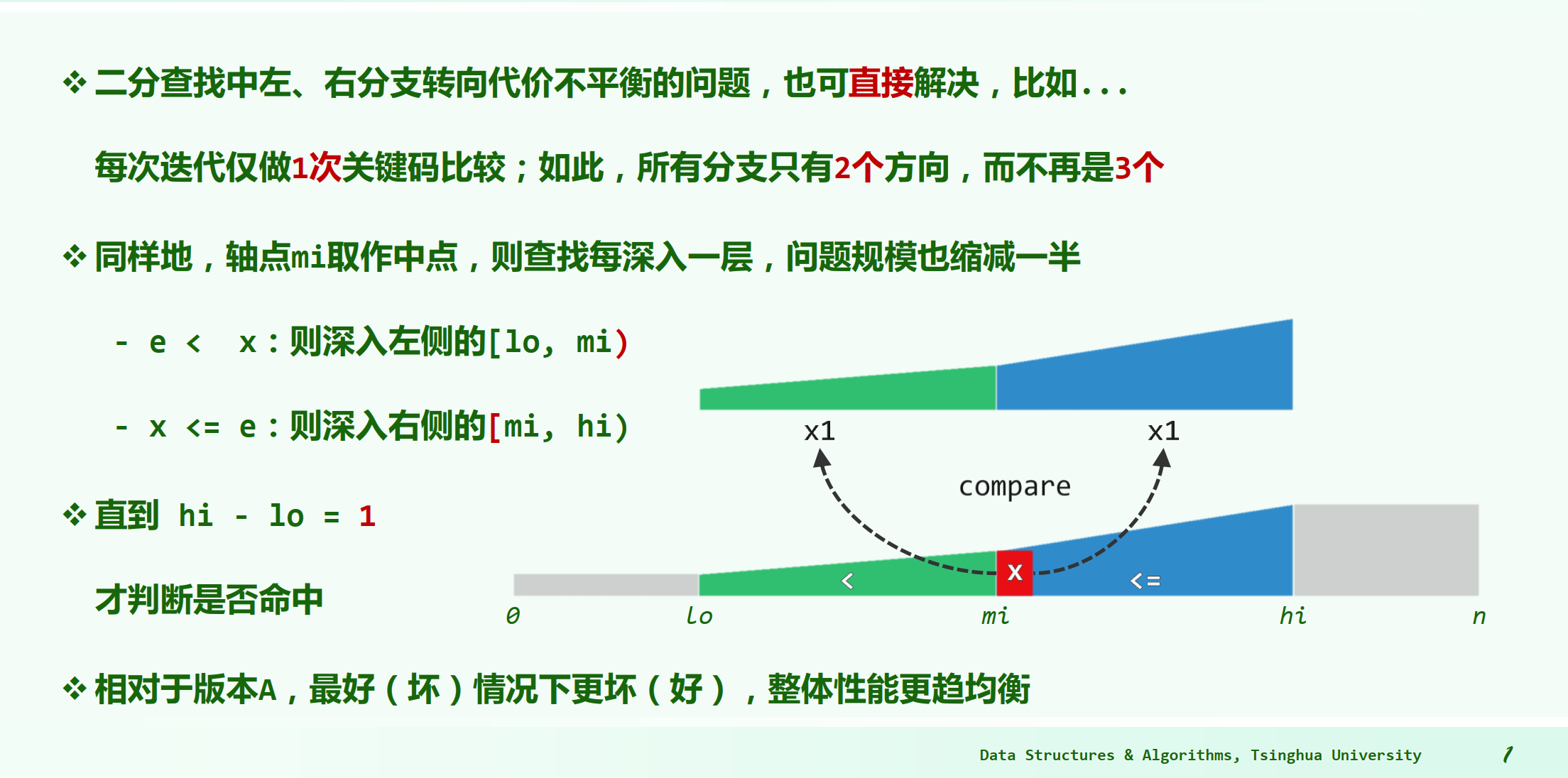
    image.png

    1. const binSearchB = (elem,e,lo,hi) => {
    2.  while (lo < hi - 1) {
    3.    //成功查找不能提前终止
    4.    const mi = (lo + hi) >> 1;
    5.    e < elem[mi] ? (hi = mi) : (lo = mi); //经比较后确定深入[lo,mi)或者[mi,hi)，将lo划为包含mi的最小秩
    6.  } //出口是 hi = lo+1
    7.  return e === elem[lo] ? lo : -1;
    8. };

    不足之处

  3. 有多个命中元素时，返回秩最大者；查找失败时，简单地返回-1，而不能指示失败的位置

    版本C

    1. //elem[0,lo)中的元素皆不大于e，elem[hi,elem.length)中的元素皆大于e
    2. const binSearchC = (elem,e,lo,hi) => {
    3.  //只有当有效区间缩减为0的时候才会终止
    4.  while (lo < hi) {
    5.    const mi = (lo + hi) >> 1;
    6.    e < elem[mi] ? (hi = mi) : (lo = mi + 1); //经比较后确定深入[lo, mi)或(mi, hi)
    7.  }
    8.  return lo - 1;
    9. };

    循环终止时， lo = hi。考查此时的元素A[lo - 1]和A[lo]：作为A[0, lo)内的最后一个
    元素， A[lo - 1]必不大于e； 作为A[lo, n) = A[hi, n)内的第一个元素， A[lo]必大于e。
    也就是说， A[lo - 1]即是原向量中不大于e的最后一个元素。因此在循环结束之后，无论成功
    与否，只需返回lo - 1即可这也是版本C与版本B的第三点差异
    image.png