树

树的相关术语

1. 位于树顶部的节点叫做根节点，没有父节点。
2. 树中的每一个元素都叫做节点，节点分为内部节点和外部节点（叶节点）。
3. 外部节点（叶节点）没有子节点。
4. 一个节点可以有祖先和后代。一个节点（除了根节点）的祖先包括父节点、祖父节点、曾祖父节点等。一个节点的后代包括子节点、孙子节点、曾孙节点等。
5. 任一节点v在通往树根沿途所经过的每个节点都是其祖先（ancestor）， v是它们的后代（descendant）。特别地，v的祖先/后代包括其本身，而v本身以外的祖先/后代称作真祖先（proper ancestor）/真后代（properdescendant）
6. 节点v孩子的总数，称其为度数或度，记做deg(v)。无孩子的节点称作叶节点（leaf） ，包括根在内的其余节点皆为内部节点。
7. 节点v所有的后代及其之间的联边称作子树（subtree）,记作subtree(v)
8. 沿每个节点v到根r的唯一通路所经过边的数目，称作v的深度（depth） ，记作depth(v)。特别地，约定根节点的深度depth(r) = 0，故属于第0层。
9. 树T中所有节点深度的最大值称作该树的高度（height），记作height(T)。仅含单节点的树的高度为0，空树高度为-1。推而广之，任一节点v所对应子树subtree(v)的高度， 亦称作该节点的高度，记作height(v)。特别地， 全树的高度亦即其根节点r的高度， height(T) = height(r)。

   二叉树

   (Binary Tree)
   二叉树中的节点最多只能有两个子节点：一个是左侧子节点，另一个是右侧子节点。这个定义有助于我们写出更高效地在树中插入、查找和删除节点的算法

   二叉搜索树

   (Binary Search Tree BST)
   只允许在左侧节点存储（比父节点）小的值，在右侧节点存储（比父节点）大的值

   遍历方式

   节点(V)、左侧子节点(L)、右侧子节点(R)

   中序遍历

   LVR
   从最小到最大的顺序访问所有节点。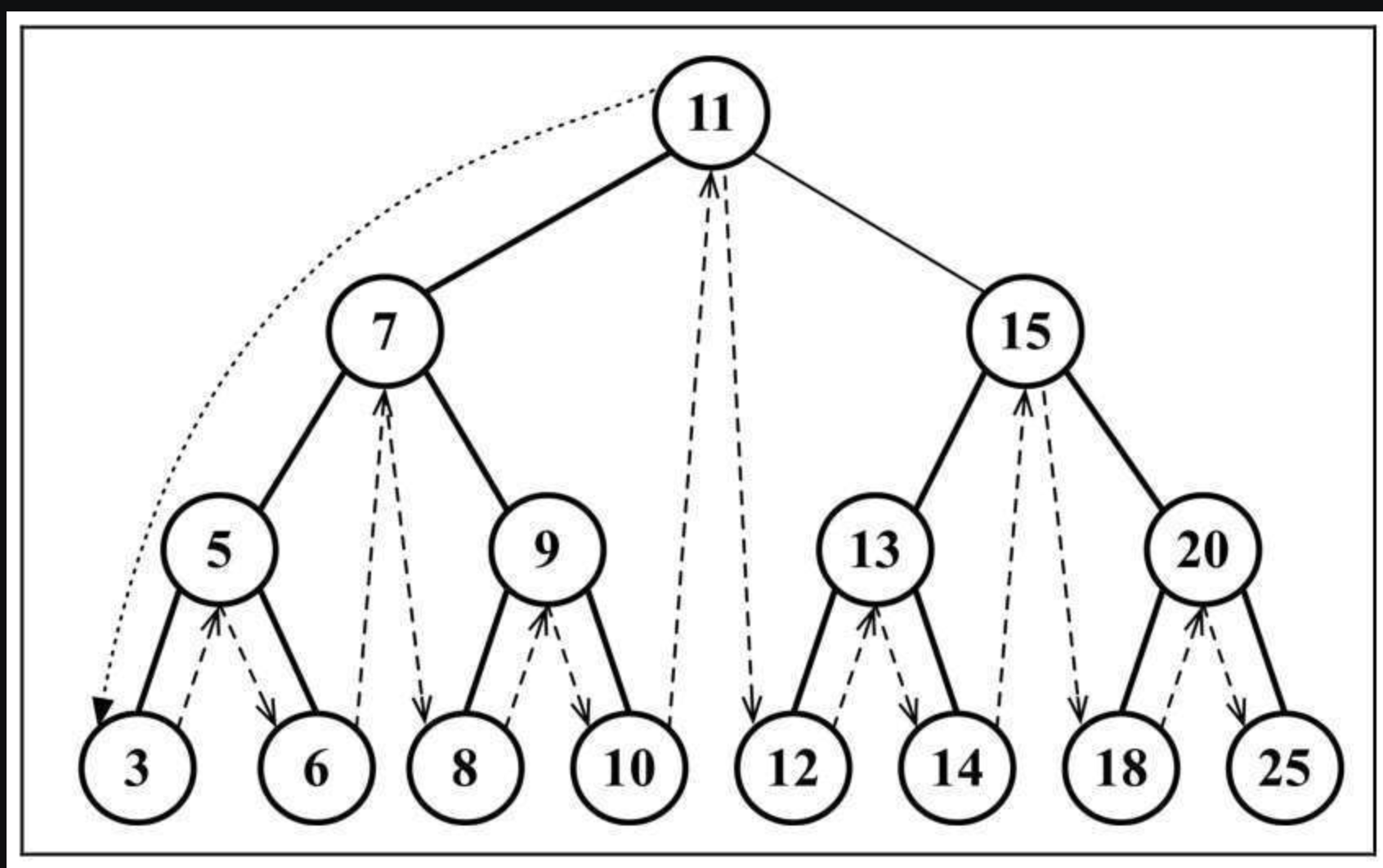
   

   先序遍历

   VLR
   优先于后代节点的顺序访问每个节点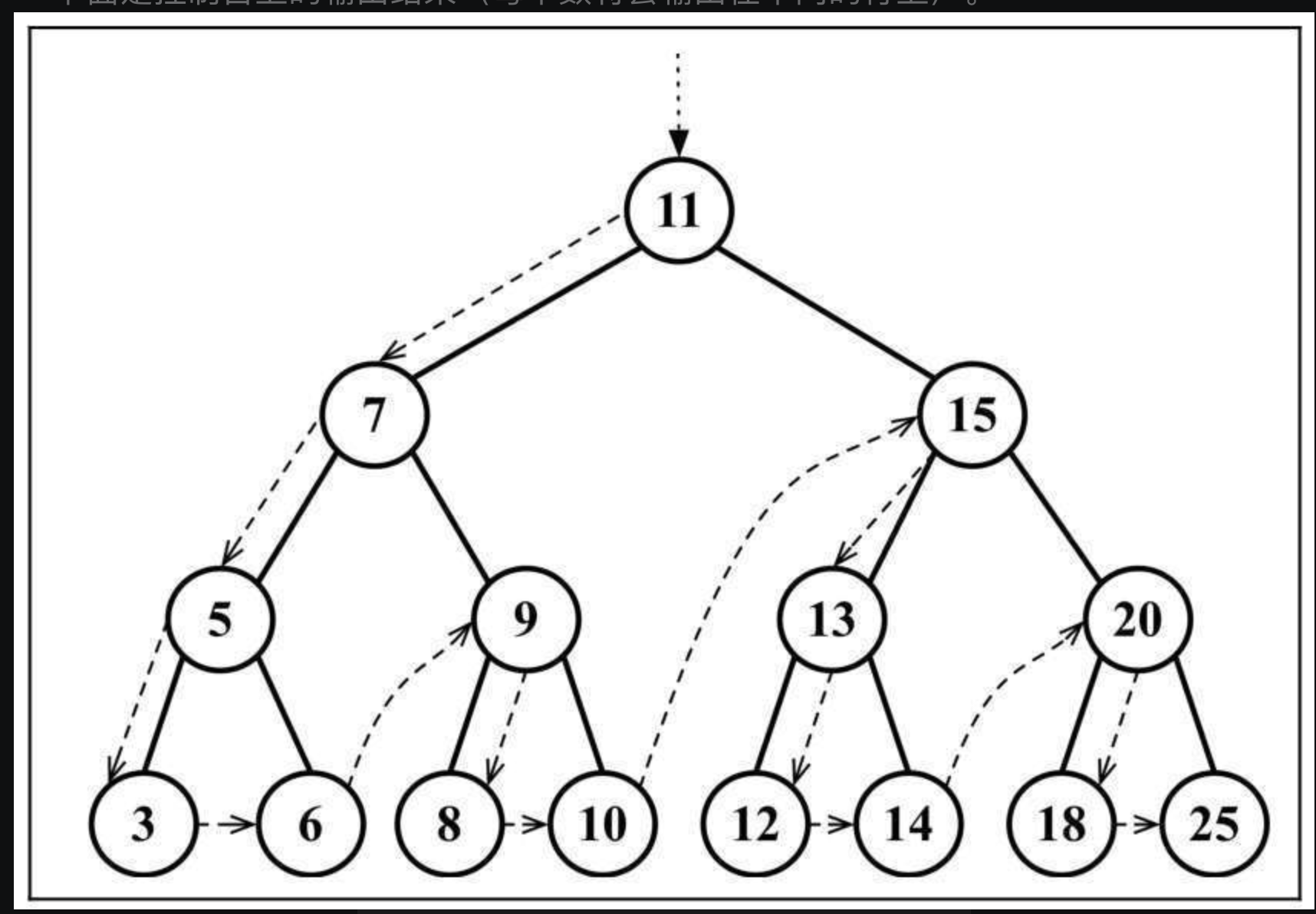
   

   后序遍历

   LRV
   先访问后代节点，再访问节点本身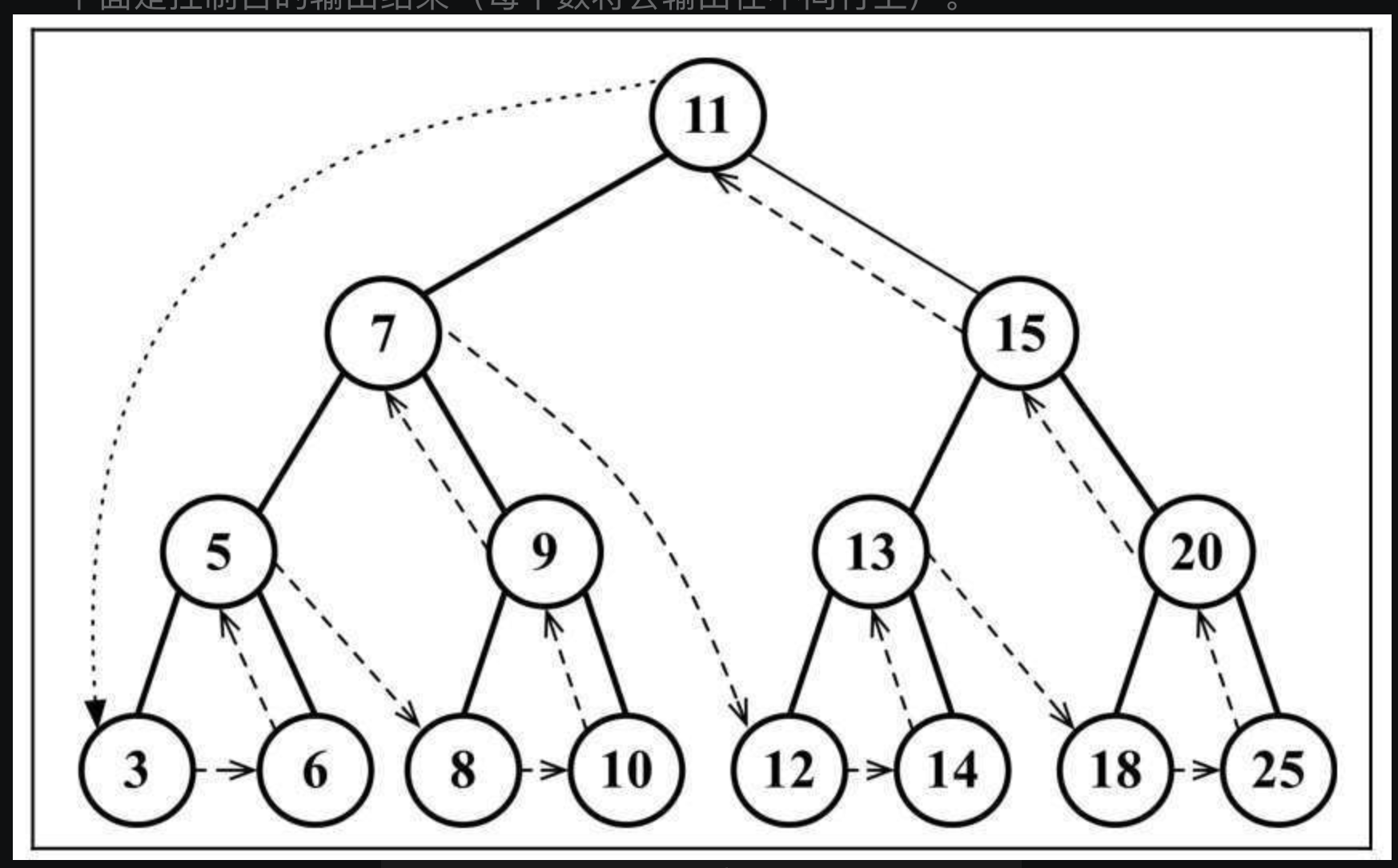
   

   自平衡树

   BST存在以下问题，树的一边可能会非常深。会引起一些性能问题，为了解决这种现象，有一种树叫做（Adelson-Velskii-Landi AVL树）
   AVL树是一种自平衡二叉搜索树，任一节点左右两侧子树的高度之差最多为1。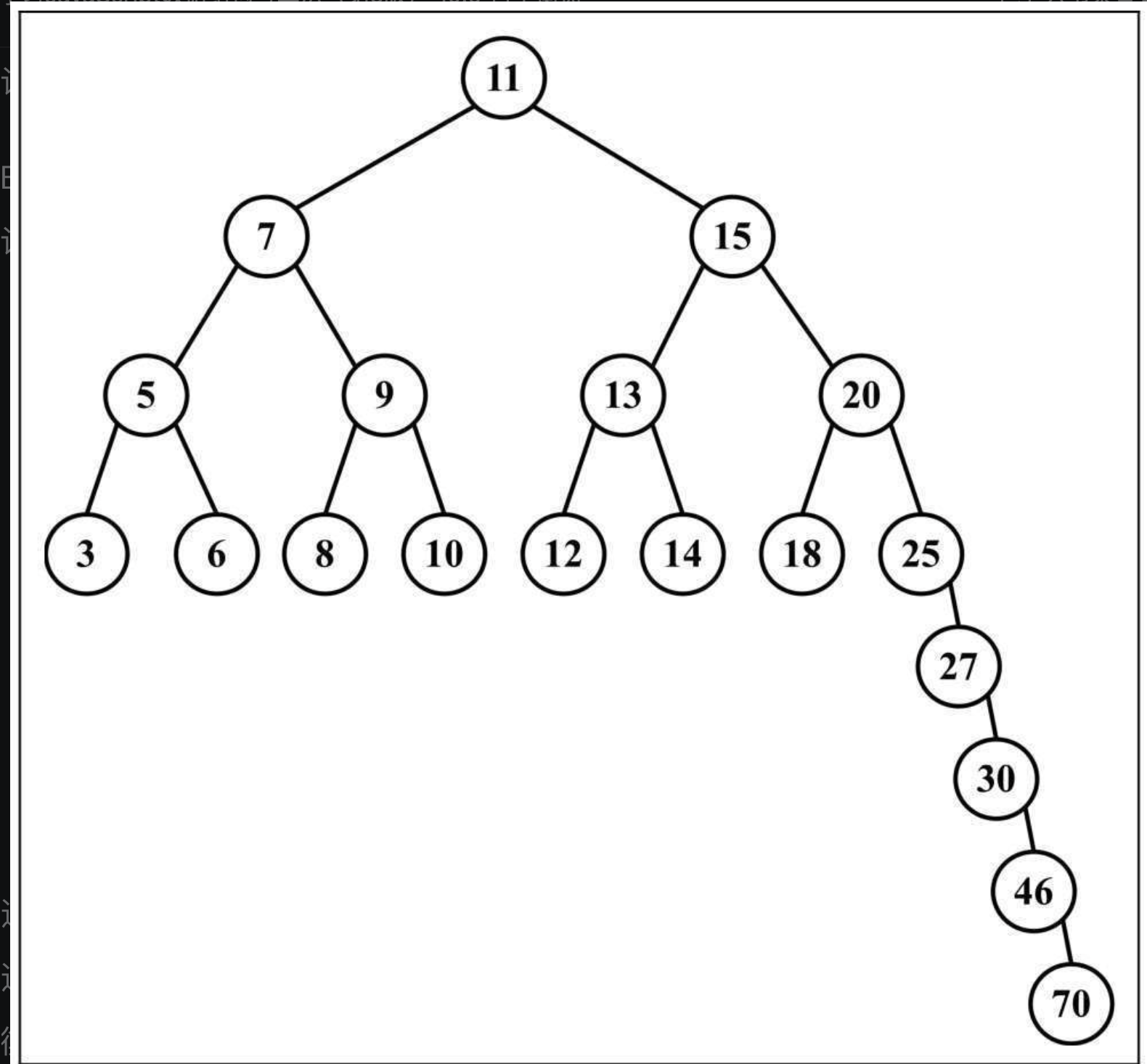
   

   节点的高度和平衡因子

   平衡操作-AVL旋转

   插入节点时，可以执行单旋转或双旋转两种平衡操作，分别对应四种场景。

   左-左(LL)：向右的单旋转

   右-右(RR)：向左的单旋转

   左-右(LR)：向右的双旋转(LL、RR)

   右-左(RL)：向左的双旋转(RR、LL)