无论就逻辑结构和算法功能而言，任何有根有序的多叉树，都可等价地转化并实现为二叉树。

1 二叉树及其表示

1.1 树

1.1.1 深度与层次

深度：沿每个节点v到根r的唯一通路所经过边的数目，称作v的深度，记作depth(v)
层次：依据深度排序，可对所有节点做分层归类。depth(r) = 0

1.1.2 祖先、后代与子树

祖先、后代：任一节点v在通往树根r沿途所经过的每个节点都是其祖先。特别地，若节点u是v的祖先且恰好比v高出一层 ，则称u是v的父亲，v是u的孩子。
子树：v所有的后代及其之间的联边称作子树，记作subtree(v)

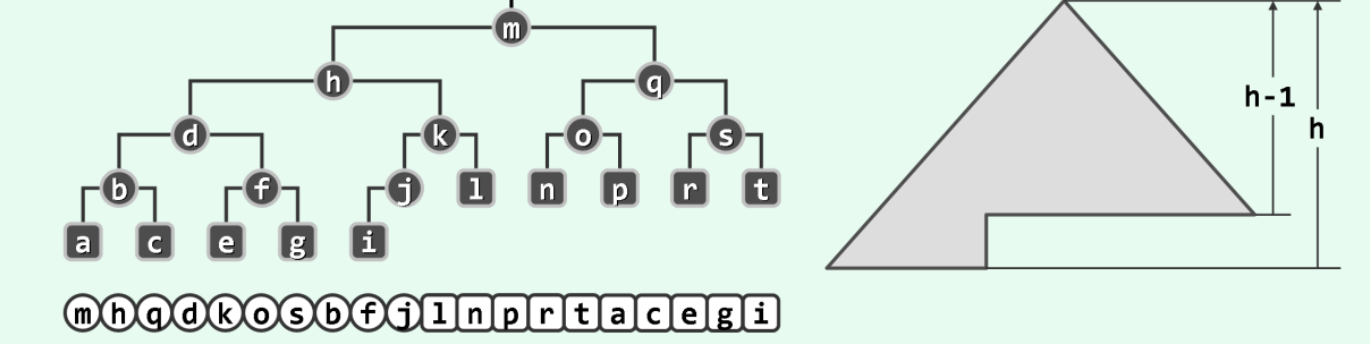
1.1.3 高度

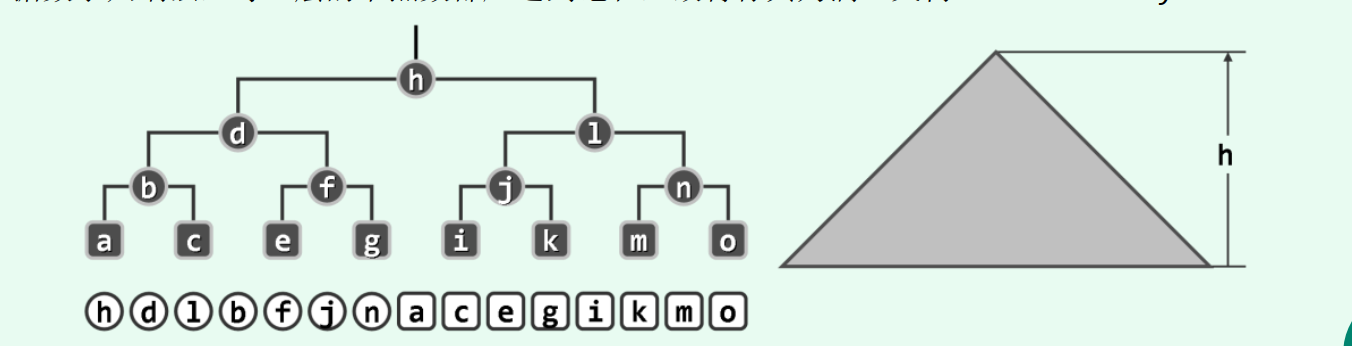
树T中所有节点深度的最大值称作该树的高度，记作height(T)。仅含单个节点的树高度为0，空树高度为-1。
任一节点v所对应子树subtree(v)的高度，亦称作该节点的高度，记作height(v)。

1.2 二叉树

二叉树中每个节点的度数均不超过2。特别地，不含一度节点的二叉树称作真二叉树。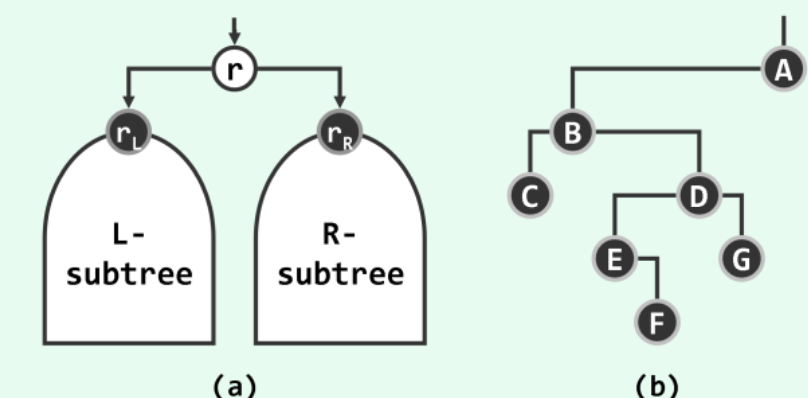
image.png

1.3 多叉树

每个节点的孩子均不超过k个的有跟树，称作k叉树。

1.3.1 父节点+孩子节点表示法

将各节点组织为向量和列表，每个元素除了保存节点本身的信息(data)外，还需要保存父节点的位置(parent)，各节点将其所有孩子组织为一个向量或列表(children)。
尽管如此可以高效地兼顾对父节点和孩子的定位，但在节点插入与删除操作频繁的场合，为了动态地维护和更新树的拓扑结构，不得不反复地遍历和调整一些节点所对应的孩子序列。然而，向量和列表等线性结构的此类操作都需耗费大量时间，势必影响到整体的效率。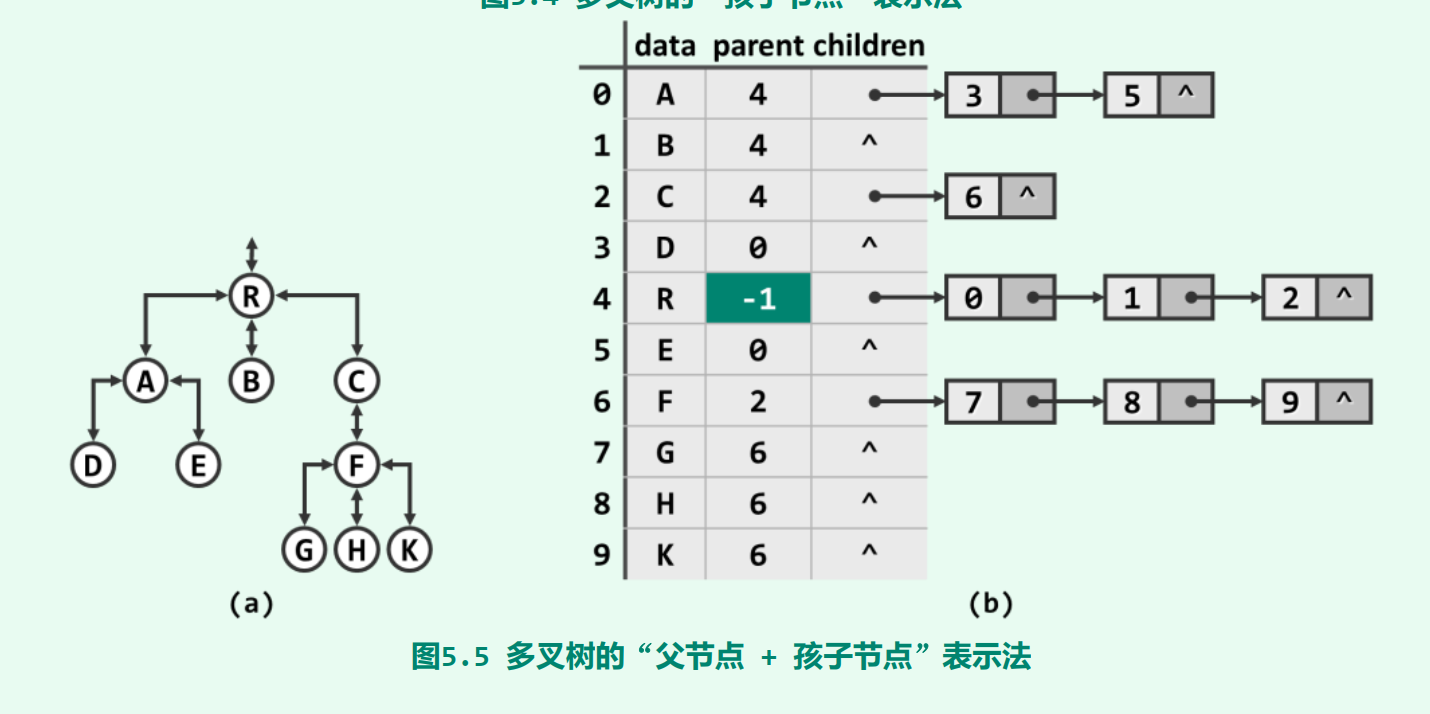
image.png

1.3.2 有序多叉树 = 二叉树

为了保证作为多叉树特例的二叉树有足够的能力表示任何一棵多叉树，我们只需给多叉树增加一项约束条件——同一节点的所有孩子之间必须具有某一线性次序。
凡符合这一条件的多叉树也称为有序树。

1.3.3 长子、兄弟

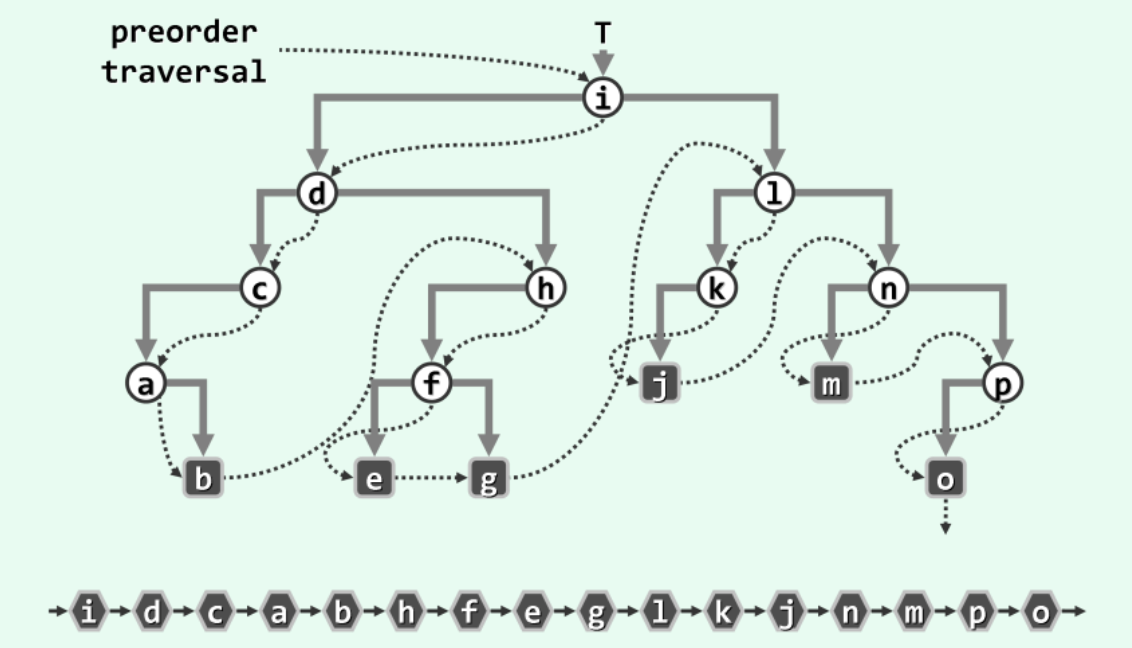
有序多叉树中任一非叶节点都有唯一的“长子” ，而且从该“长子” 出发，可按照预先约定或指定的次序遍历所有孩子节点。如下图所示，为每个节点设置两个指针，分别指向其“长子”（实线） 和下一“兄弟”（虚线） 。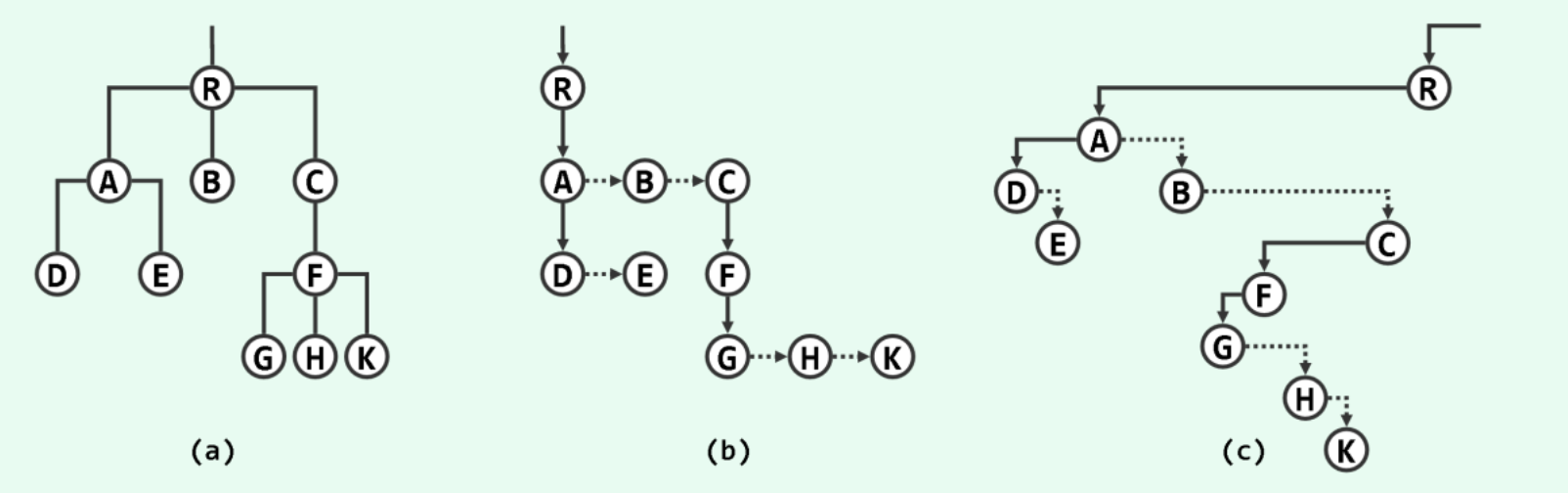
image.png

2 编码树

2.1 二进制编码

信息被转换为二进制形式的过程称作编码（ encoding）； 反之， 经信道抵达目标后再由二进制编码恢复原始信息的过程称作解码。

2.1.1 生成编码表

每一编码表都是从字符集到编码表的一个单射，编码就是对信息文本中各字符逐个实施这一映射的过程，而解码则是逆向映射的过程。
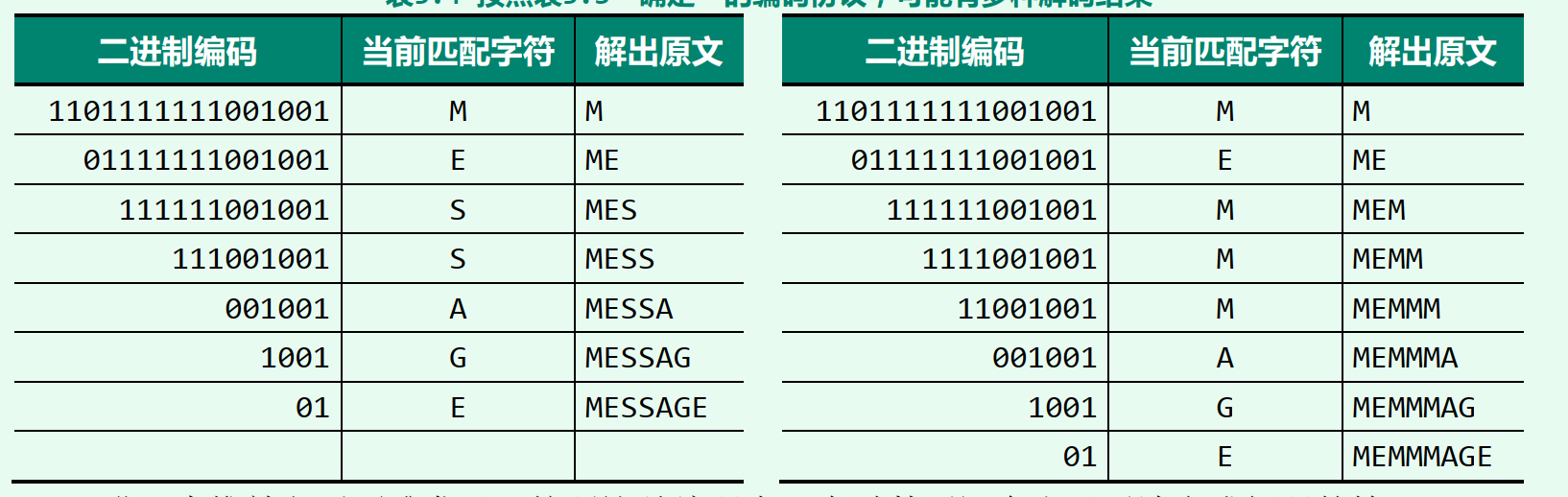
image.png

2.1.2 解码歧义

image.png
image.png

2.1.3 前缀无歧义编码

任何两个原始字符所对应的二进制编码，相互都不得是前缀。简称PFC编码。

2.2 二叉编码树

2.2.1 根通路与节点编码

从根节点到每个节点的唯一通路，可以为各节点v赋予一个互异的二进制串。

2.2.2 PFC编码树

只要所有字符都对应叶节点（不存在父子（前缀）关系），就不会导致解码歧义。
图b中M是S的父节点，存在前缀现象。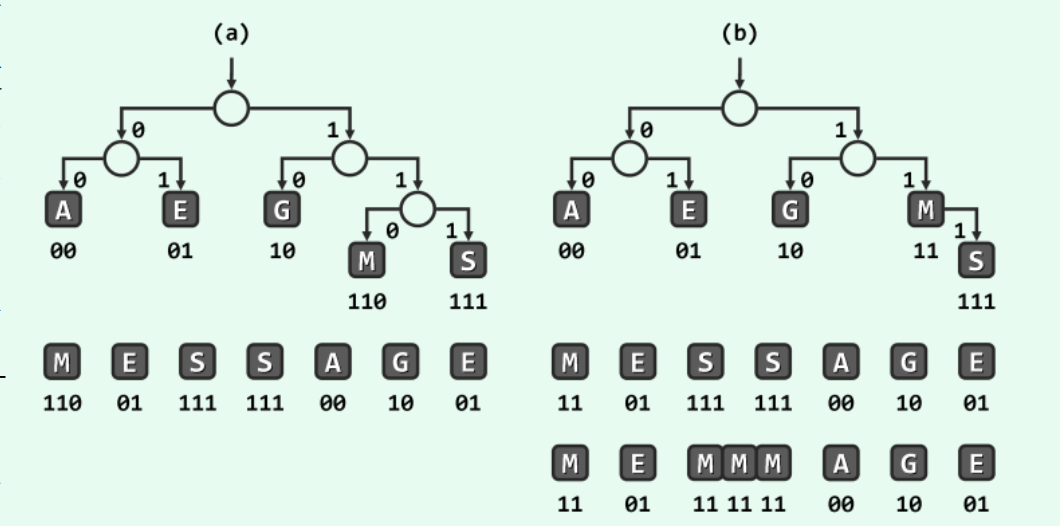
image.png

2.2.3 基于PFC编码树的解码

持续从树根开始对二进制编码进行扫描，取出对应的字符。

2.2.4 PFC编码树的构造

3 二叉树的实现

参考二叉树实现项目地址
一旦有节点加入或离开二叉树，则更新其所有祖先的高度。

3.1 二叉树节点

3.2 二叉树节点操作接口

3.3 二叉树

4 遍历

此过程等效于将半线性的树形结构，转化为线性结构。
节点：V、左孩子L、右孩子R
在遍历中，左孩子始终优于右孩子
VLR(先序遍历)、LVR(中序遍历)、LRV(后序遍历)

4.1 递归式遍历

4.1.1 先序遍历VLR

先遍历根节点，然后左子树，然后右子树。
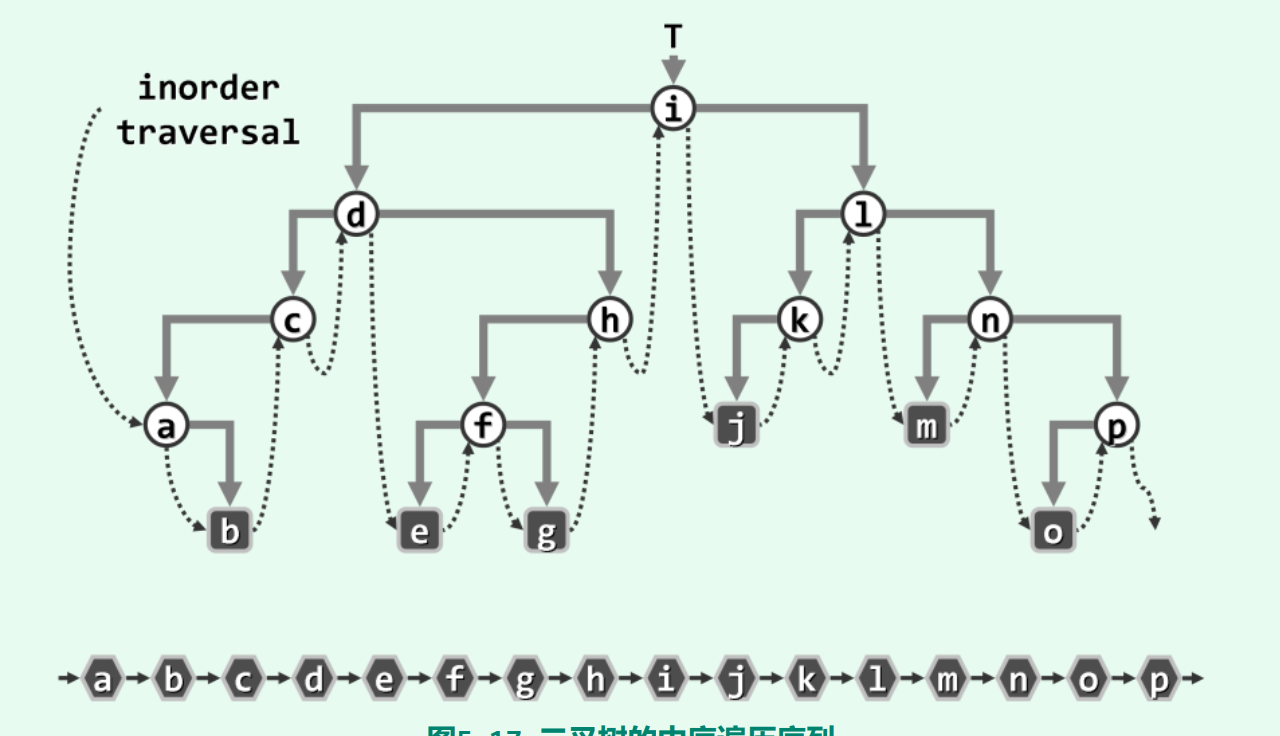
image.png

4.1.2 中序遍历LVR

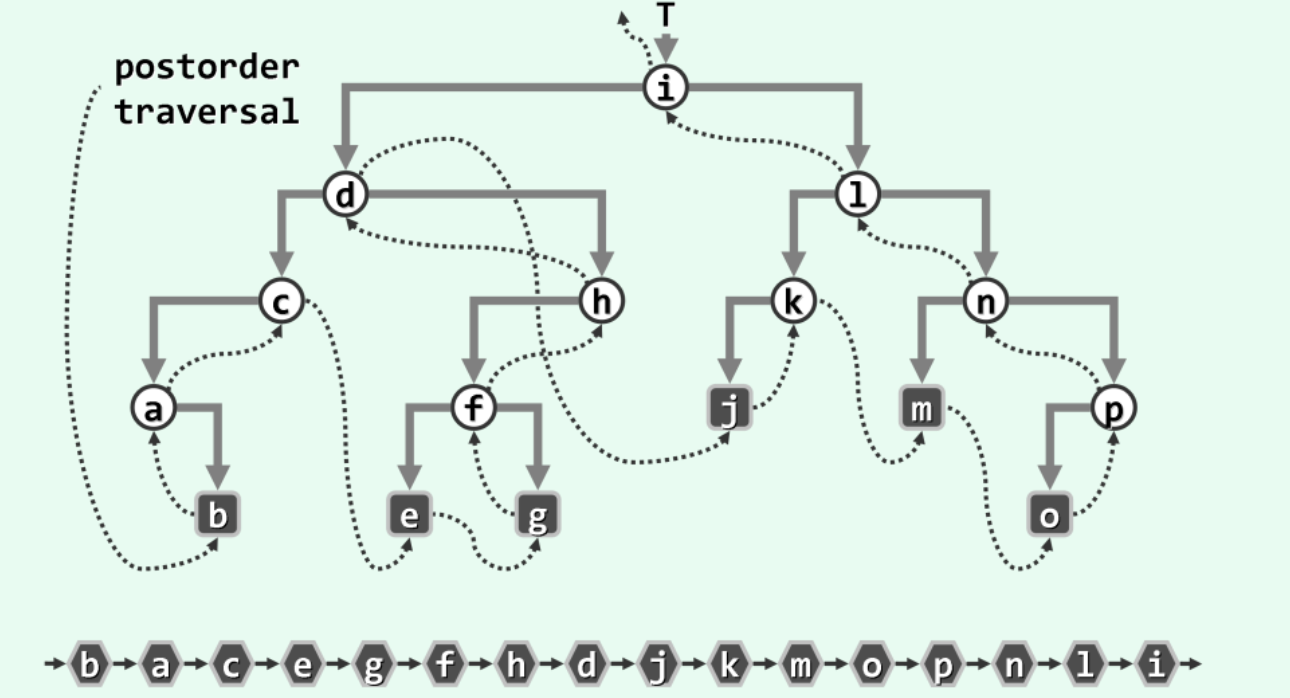
image.png

4.1.3 后序遍历LRV

节点的左右子树都访问完后，才访问节点的值。
image.png

4.2 迭代版先序遍历

先序遍历序列可分解为两段： 沿最左侧通路自顶而下访问的各节点， 以及自底而上遍历的对应右子树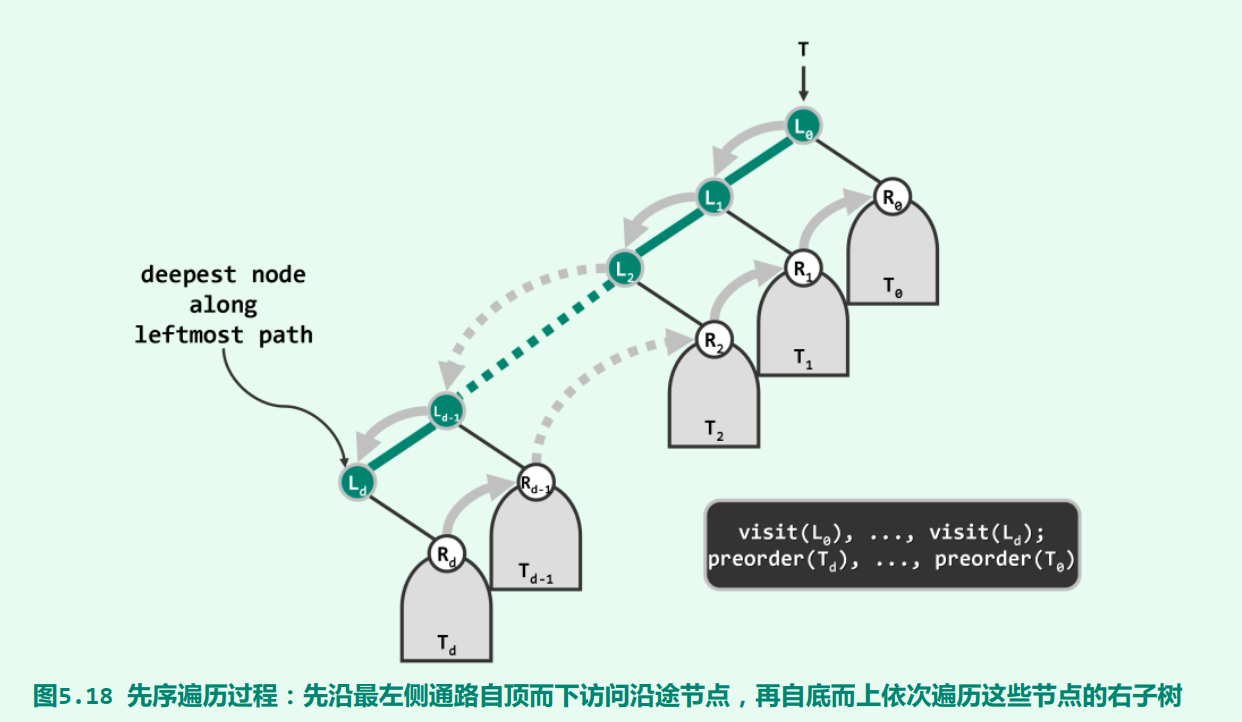
image.png

4.3 迭代版中序遍历

若最后一个左子节点没有子节点，相当于它的左子树已经访问过了。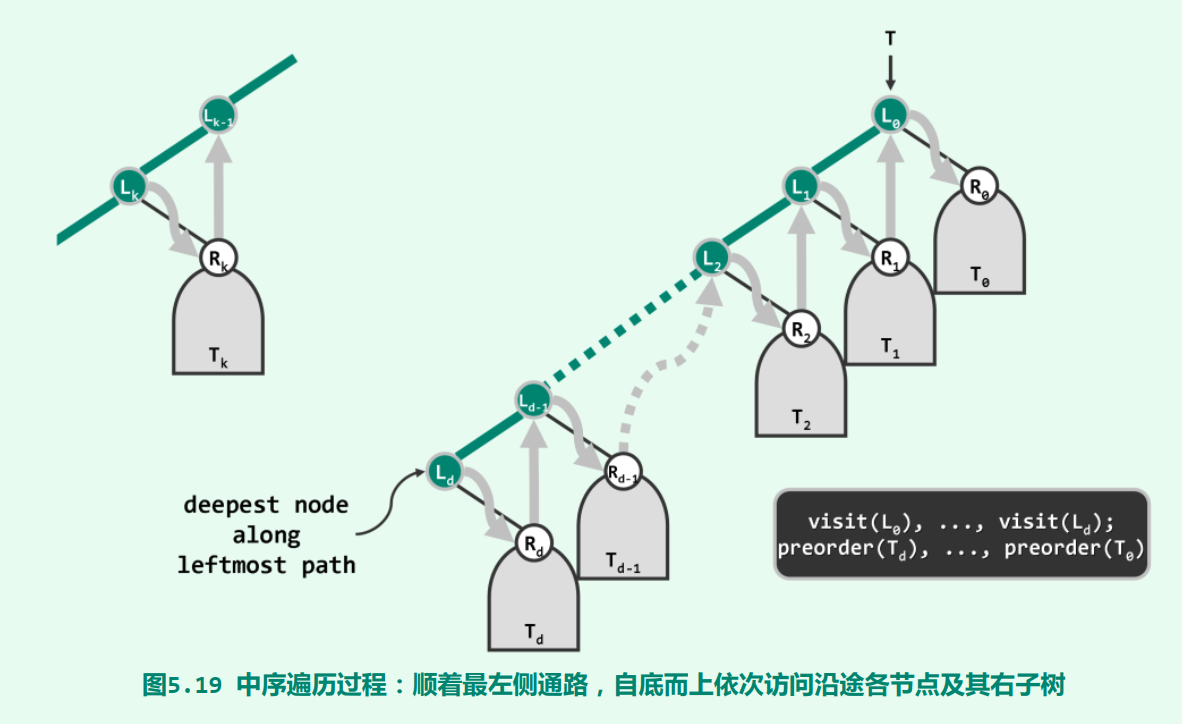
image.png

4.4 迭代版后序遍历

与先序与中序遍历类似地， 自底而上地沿着该通路， 整个后序遍历序列也可分解为若干个片段。每一片段，分别起始于通路上的一个节点，并包括三步： 访问当前节点(左子节点)， 遍历以其右兄弟（若存在）为根的子树，以及向上回溯至其父节点（若存在）并转入下一片段。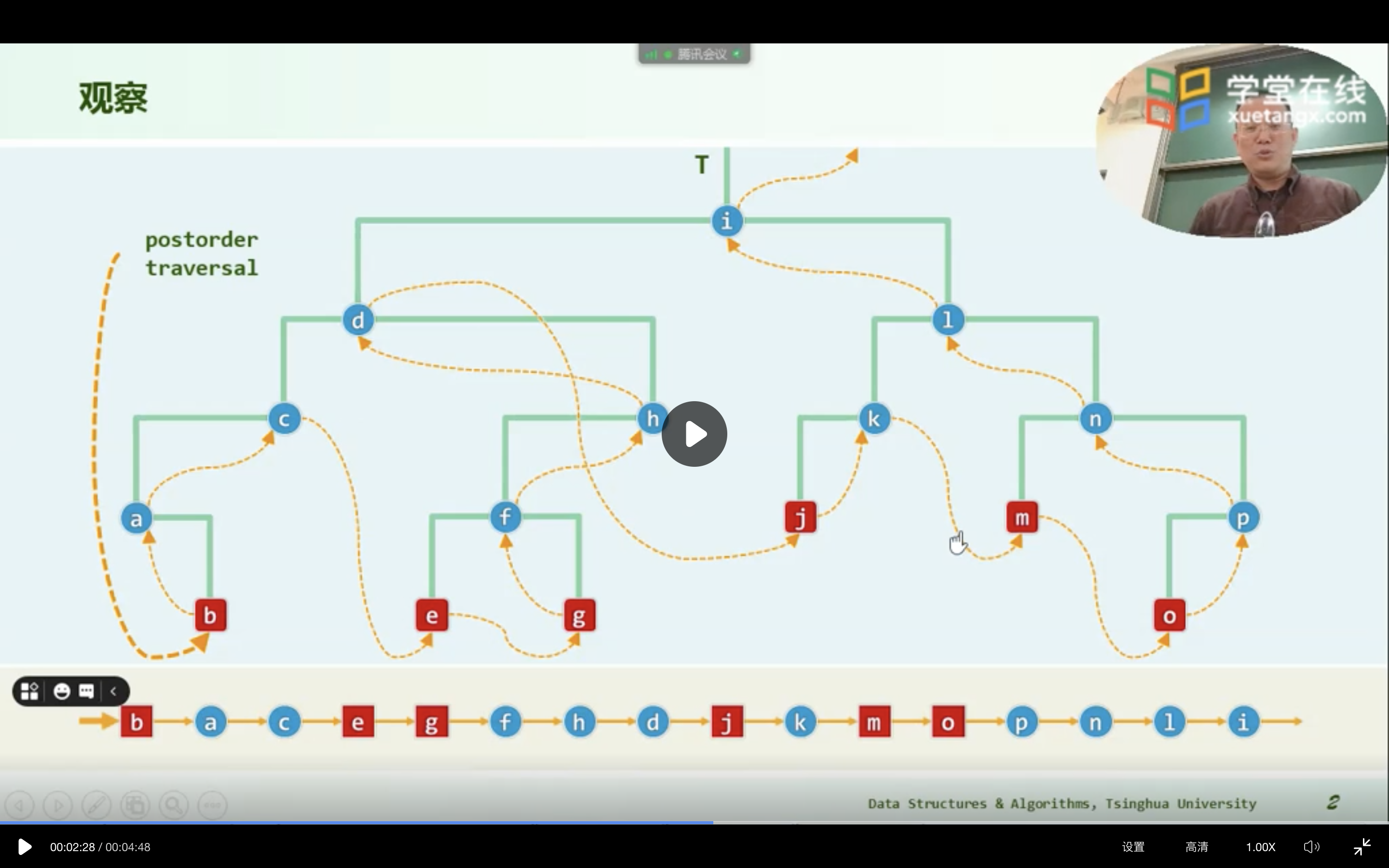
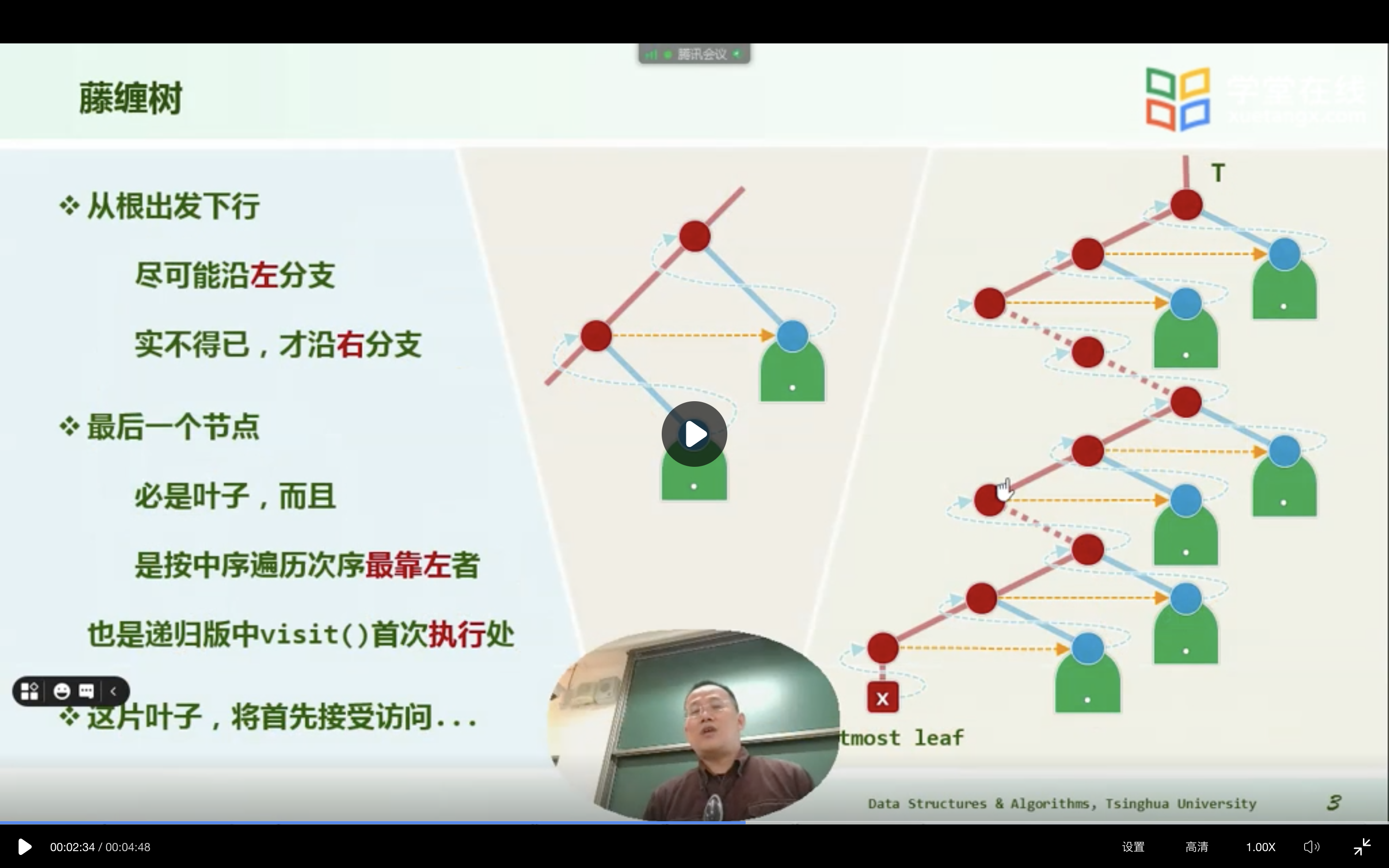
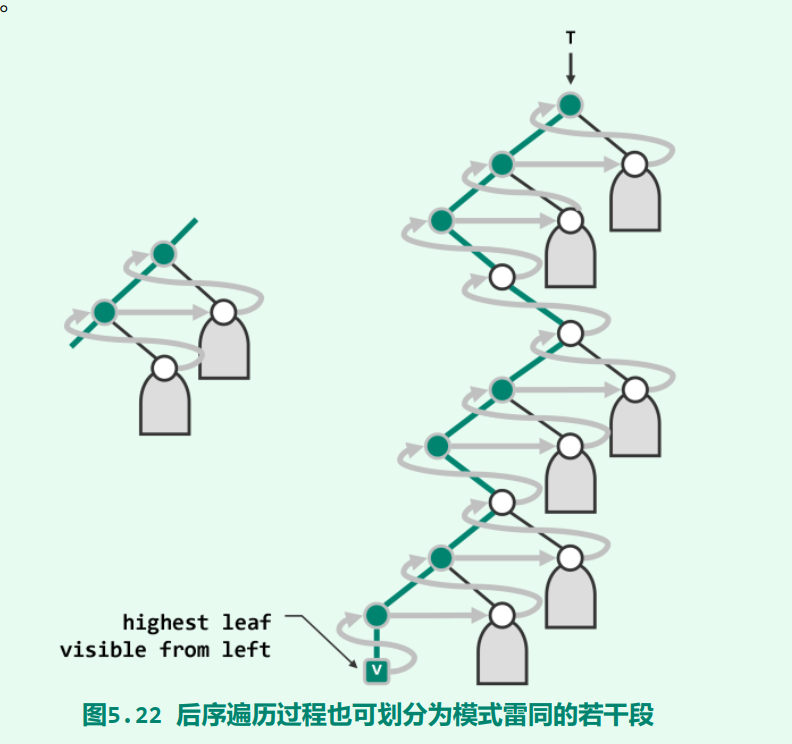
image.png
image.png
image.png
最右边依然是右子树，因为左子节点（红色部分）会变成“藤”

4.5 层次遍历

确定节点访问次序的原则可概括为“先上后下、先左后右”。
先访问树根， 再依次是左孩子、右孩子、左孩子的左孩子、左孩子的右孩子、右孩子的左孩子、右孩子的右孩子、 …，依此类推。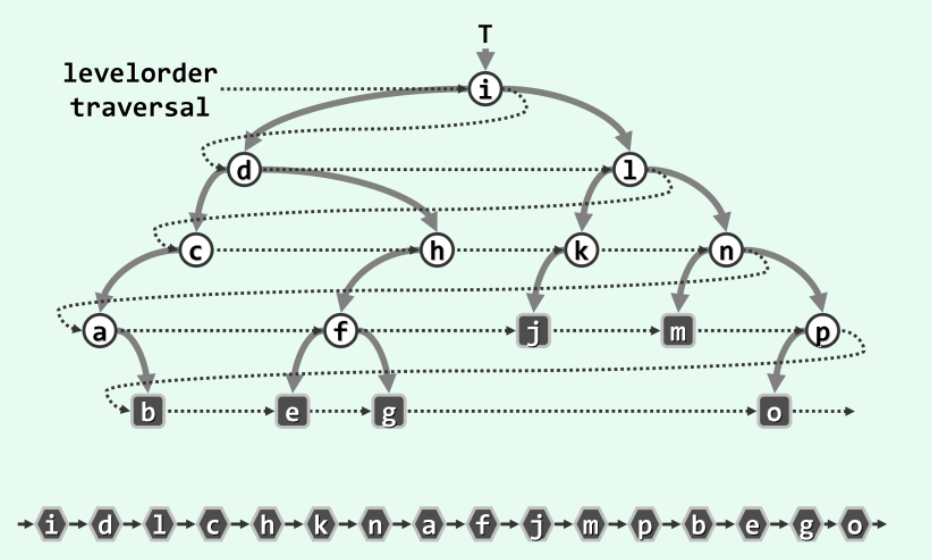
image.png

4.5.1 算法实现

每一次迭代中，首先取出并访问队首节点，然后其左、右孩子将顺序入队。一旦在试图进入下一迭代前发现队列为空，遍历即告完成。

4.5.2 完全二叉树

层次遍历的次数为n，若在对某棵二叉树的层次遍历过程中，前n/2次迭代中都有左孩子入队，且前[n/2]-1次迭代中都有右孩子入队。则称为完全二叉树(CBT complete binary tree)
叶节点只能出现在最底层的两层，且最底层叶节点均处于次底层叶节点的左侧。
image.png

4.5.3 满二叉树

image.png

5 Huffman编码