1. 伸展树
伸展树无需时刻都严格地保持全树的平衡, 但却能够在任何足够长的真实操作序列中,保持分摊意义上的高效率。伸展树也不需要对基本的二叉树节点结构, 做任何附加的要求或改动, 更不需要记录平衡因子或高度之类的额外信息,故适用范围更广。
1.1 局部性
- 刚刚被访问过的节点, 极有可能在不久之后再次被访问到。
- 将被访问的下一节点, 极有可能就处于不久之前被访问过的某个节点的附近。
因此,只需将刚被访问的节点,及时地“转移”至树根(附近), 即可加速后续的操作。
1.2 逐层伸展
一种直接方式是: 每访问过一个节点之后(无论查找或插入,甚至“删除” ), 随即反复地以它的父节点为轴,经适当的旋转将其提升一层,直至最终成为树根。但会有很大的缺陷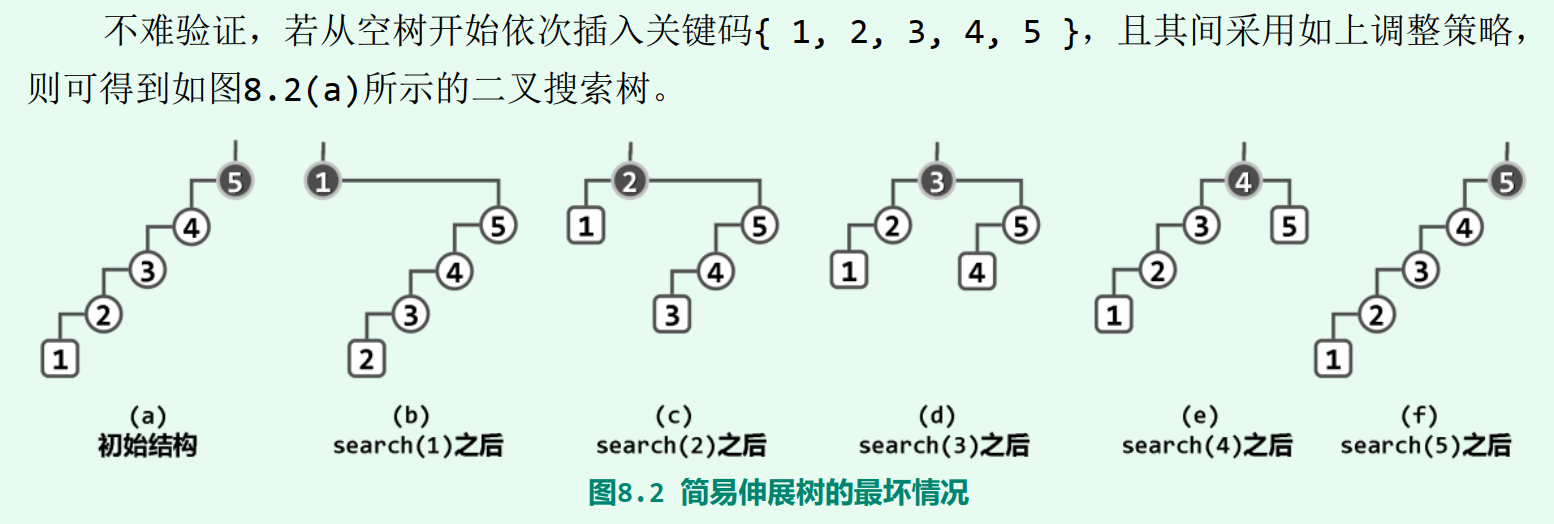
1.3 双层伸展
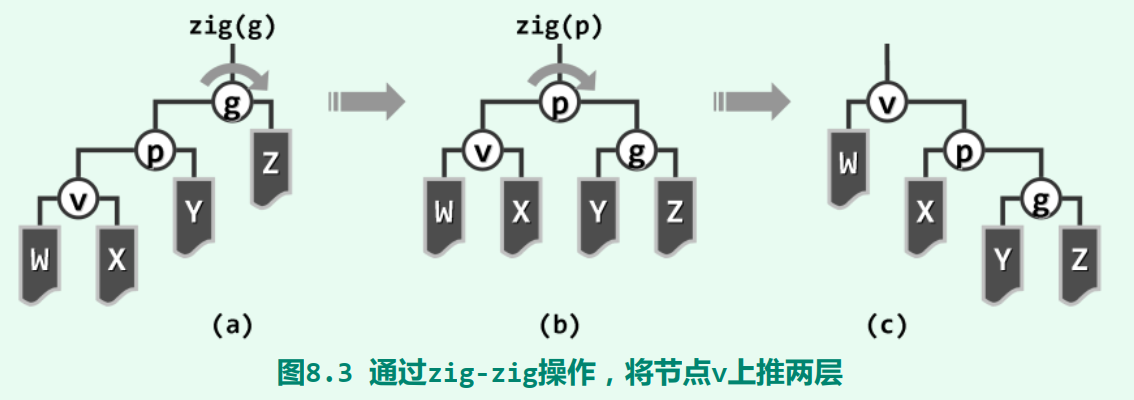
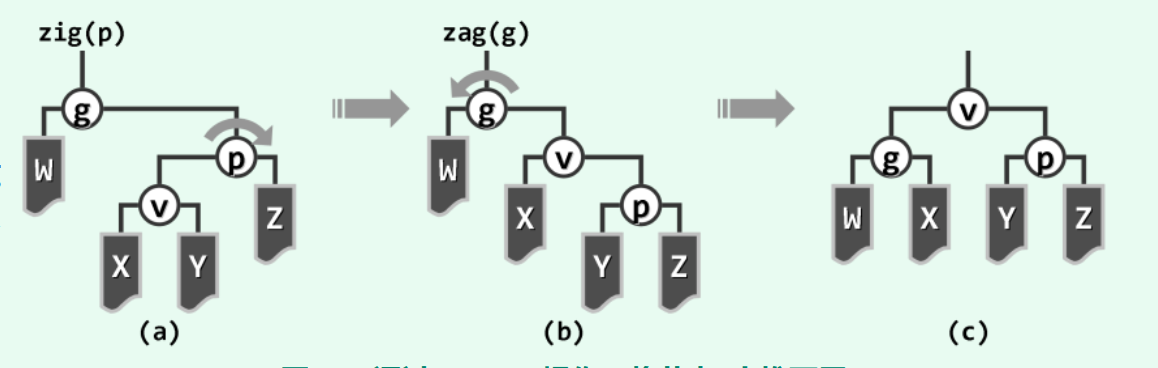
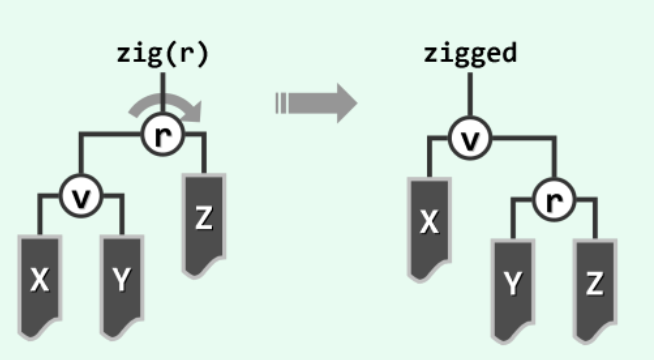
具体地,每次都从当前节点v向上追溯两层(而不是仅一层),并根据其父亲p以及祖父g的相对位置,进行相应的旋转
1.3.1 zig-zig/zag-zag
1.3.2 zig-zag/zag-zig
1.3.3 zig-zag
1.3.4 zig/zag
1.4 查找算法的实现
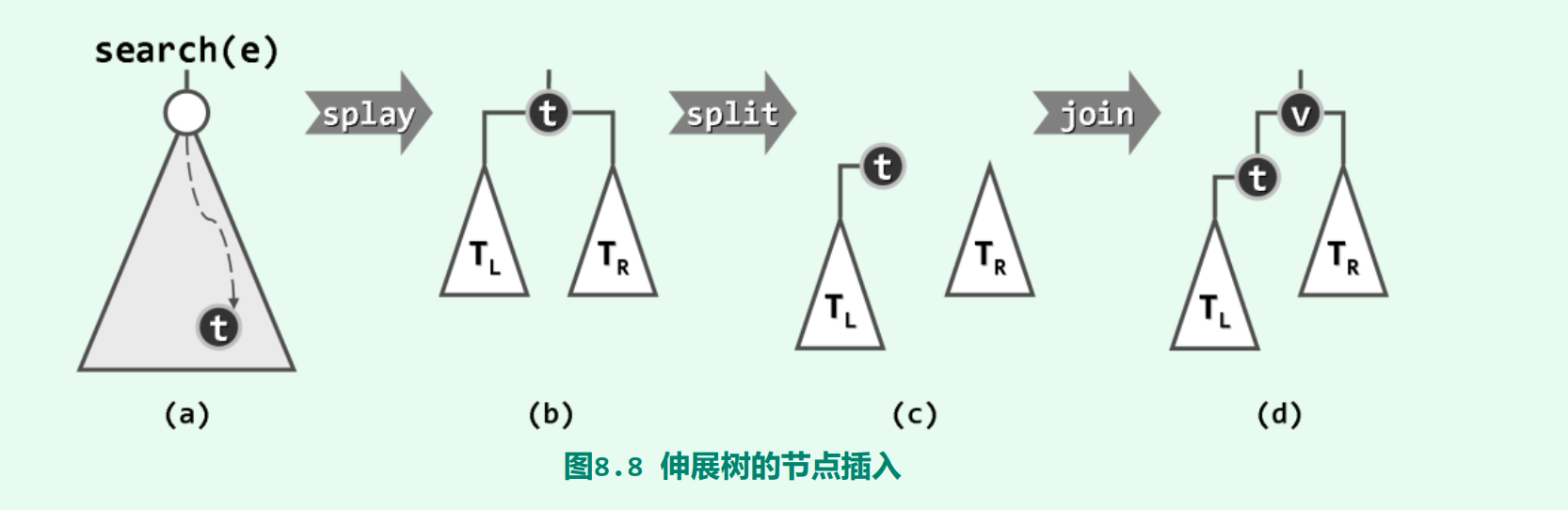
1.5 插入算法的实现
1.6 删除算法的实现
2. B-树
多路搜索树
由于各节点的分支数介于[m/2]至m之间,故m阶B-树也称作(m/2, m)-树,如(2, 3)-树、(3, 6)-树或(7, 13)-树等
对应的各节点的关键码数量介于 [m/2] -1,m-1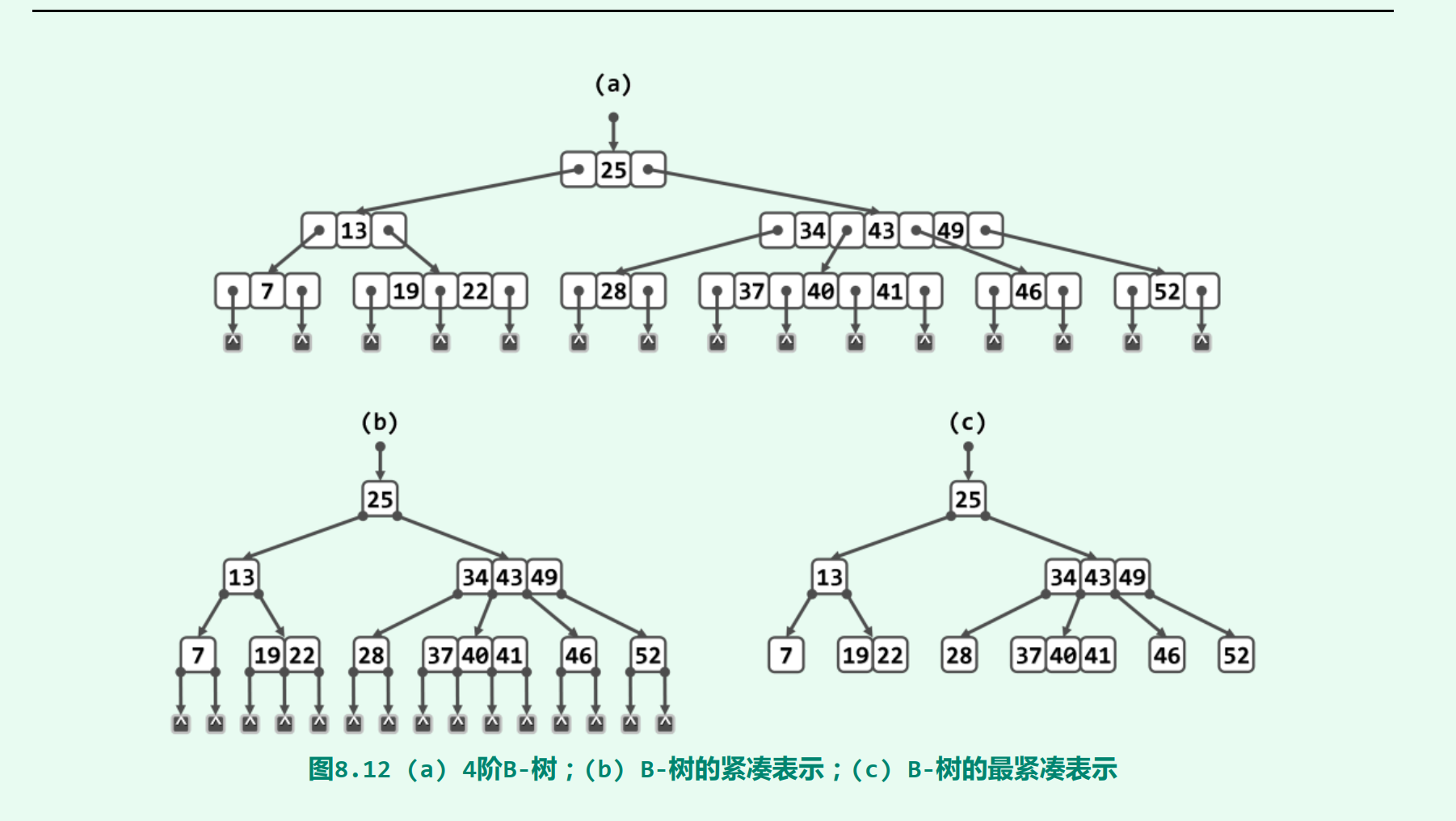
2.1 多路平衡查找
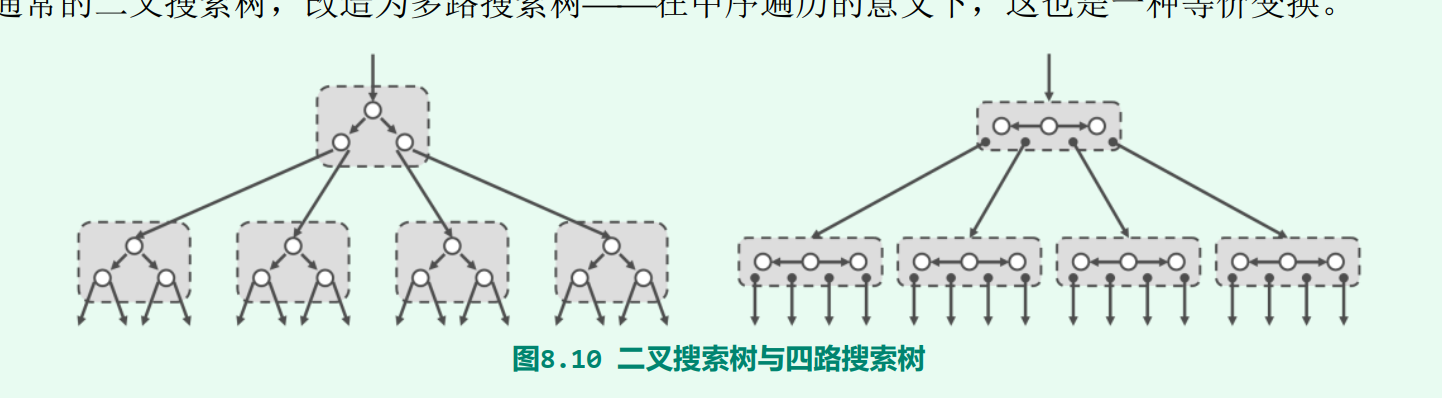
一般地,以k层为间隔如此重组,可将二叉搜索树转化为等价的2^k路搜索树,统称多路搜索树(multi-way search tree)。
所谓m阶B-树(B-tree), 即m路平衡搜索树(m >= 2)
每个内部节点都存有不超过m - 1个关键码, 以及用以指示对应分支的不超过m个引用
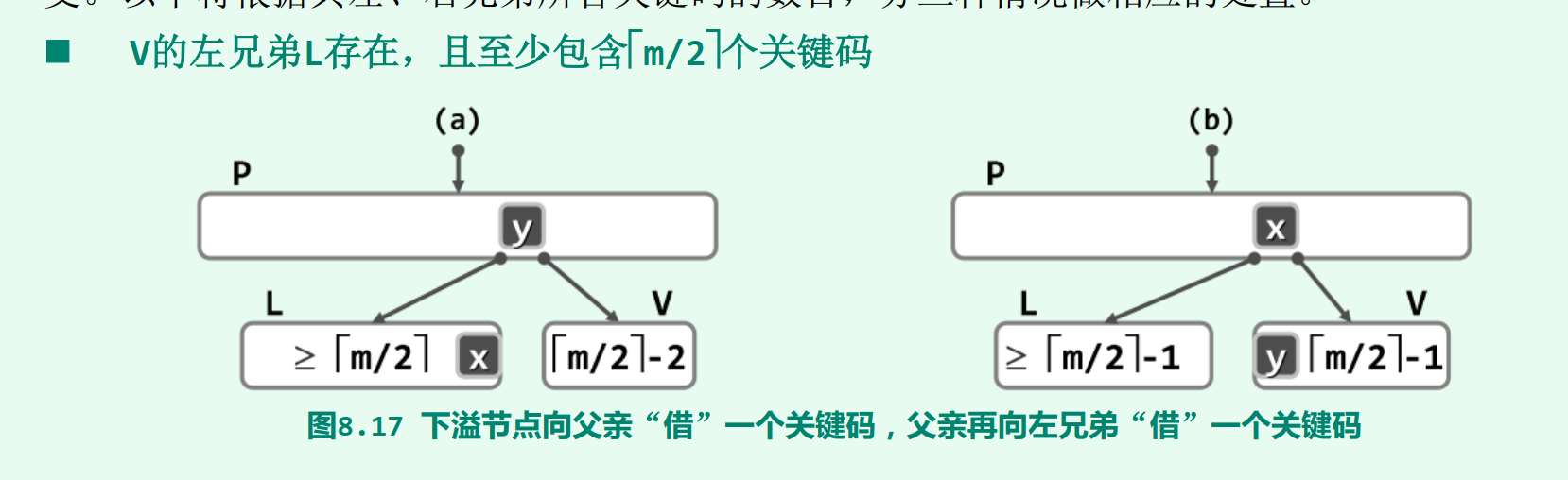
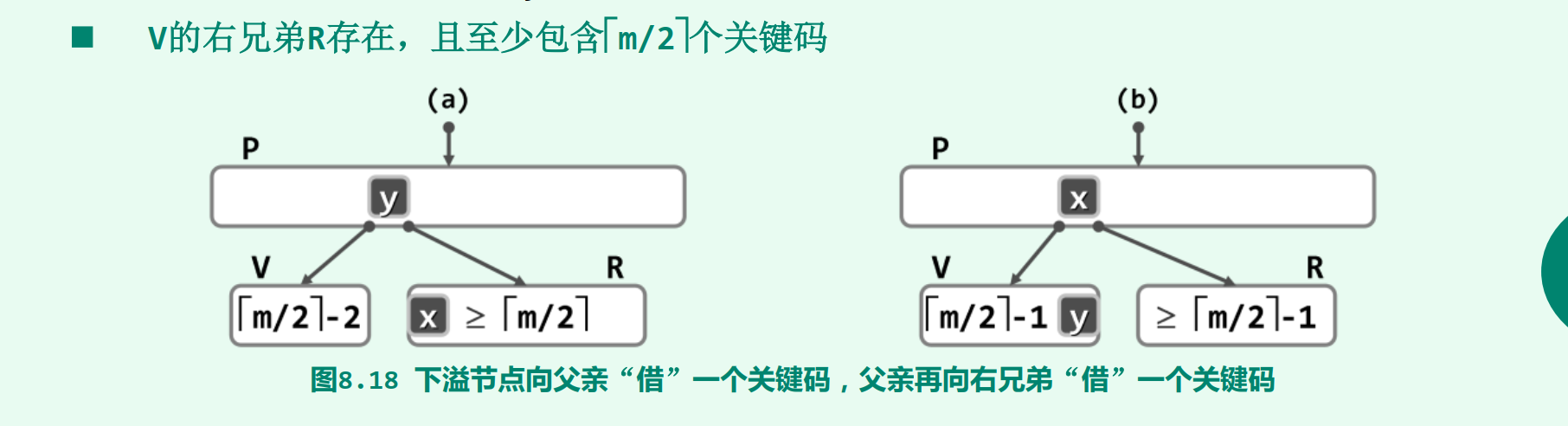
反过来,各内部节点的分支数也不能太少。具体地,除根以外的所有内部节点,都应满足:n + 1 >=m/2
由于各节点的分支数介于m/2至m之间,故m阶B-树也称作(m/2, m)-树
2.2 插入
2.3 删除
2.3.1 下溢
3. 红黑树
AVL树尽管可以保证最坏情况下的单次操作速度,但需在节点中嵌入平衡因子等标识;更重要的是, 删除操作之后的重平衡可能需做多达(logn)次旋转, 从而频繁地导致全树整体拓扑结构的大幅度变化。
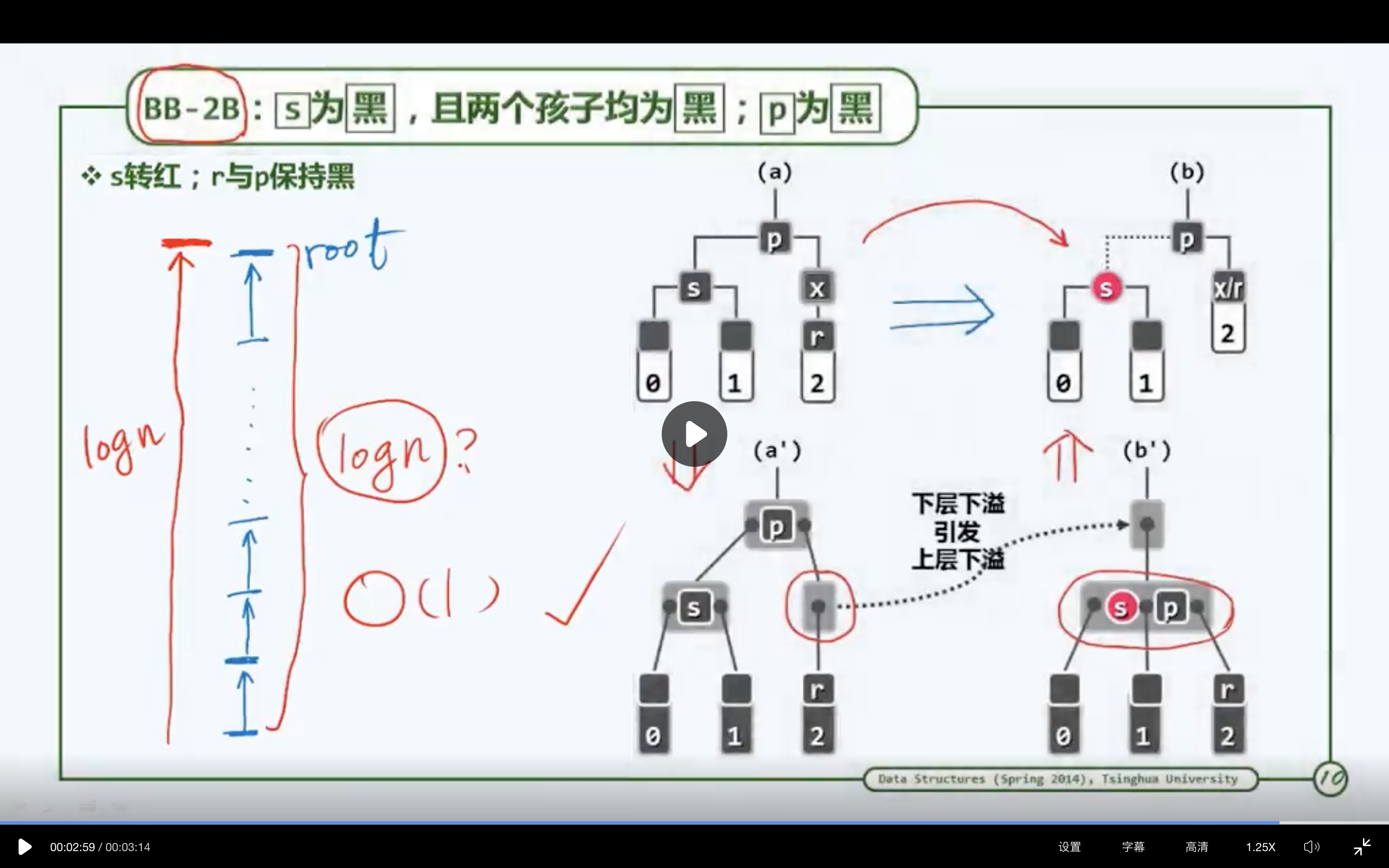
红黑树即是针对后一不足的改进。通过为节点指定颜色, 并巧妙地动态调整,红黑树可保证:在每次插入或删除操作之后的重平衡过程中, 全树拓扑结构的更新仅涉及常数个节点。尽管最坏情况下需对多达(logn)个节点重染色,但就分摊意义而言仅为O(1)个
红黑树所采用的“适度平衡”标准,可大致表述为: 任一节点左、右子树的高度,相差不得超过两倍。
每棵红黑树都等价于一棵(2,4)-树
以圆形、正方形和八角形表示红黑树的红节点、黑节点和颜色未定节点,以扁平长斱形表示B-树节点)
3.1 概述
外部节点即为值为空的假想式节点。为了将二叉树扩展为真二叉树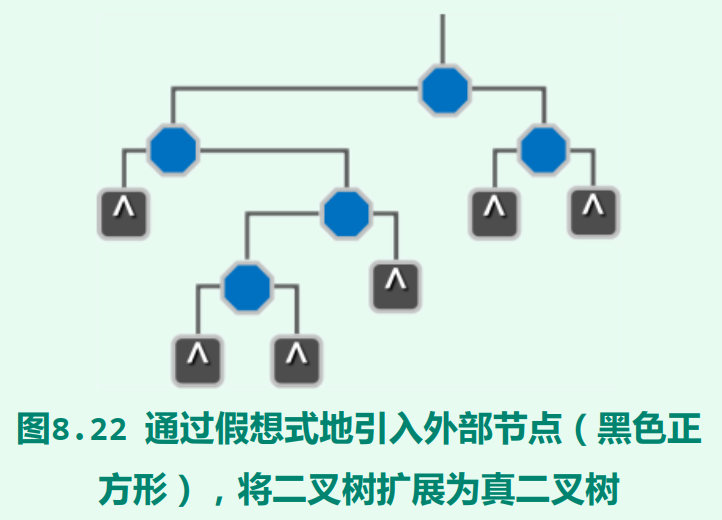
满足以下条件的二叉搜索树即为红黑树:
- 树根始终为黑色
- 外部节点均为黑色
- 除外部节点外的其余节点若为红色,其孩子节点必为黑色
- 从任一外部节点到根节点的沿途,黑节点的数目相等。(控制节点不能一直为黑色,控制黑深度和黑高度的值。新插入的节点初始都为红色)
由此可知,在从根节点通往任一节点的沿途, 黑节点都不少于红节点。除去根节点本身,沿途所经黑节点的总数称作该节点的黑深度。根节点的黑深度为0
在从任一节点通往其任一后代外部节点的沿途,黑节点的总数亦必相等。除去(黑色)外部节点,沿途所经黑节点的总数称作该节点的黑高度(black height) 。如此,所有外部节点的黑高度均为0,其余依此类推
根节点的黑高度亦称作全树的黑高度,在数值上与外部节点的黑深度相等。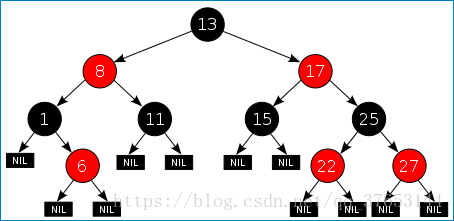
3.2 提升变换
每一个超级节点至少拥有两个分支,至多拥有四个分支
通往黑节点的边对黑高度有贡献 ,用实线表示。通往红节点的边对黑高度没有贡献,用虚线表示。
(圆形为红色节点,正方形为黑色节点,八角形表示颜色未定节点。扁长方形表示B树节点)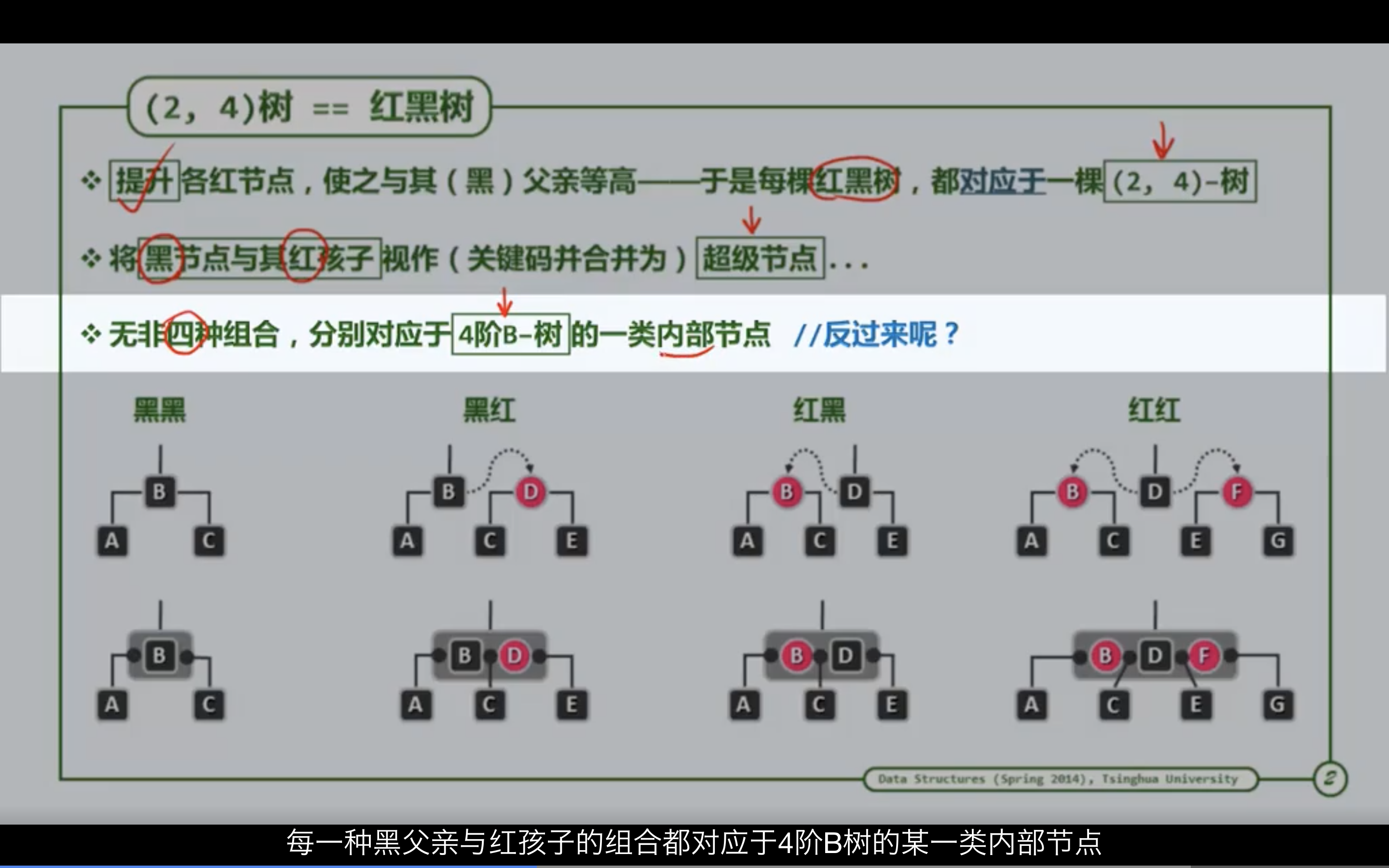
3.3 插入
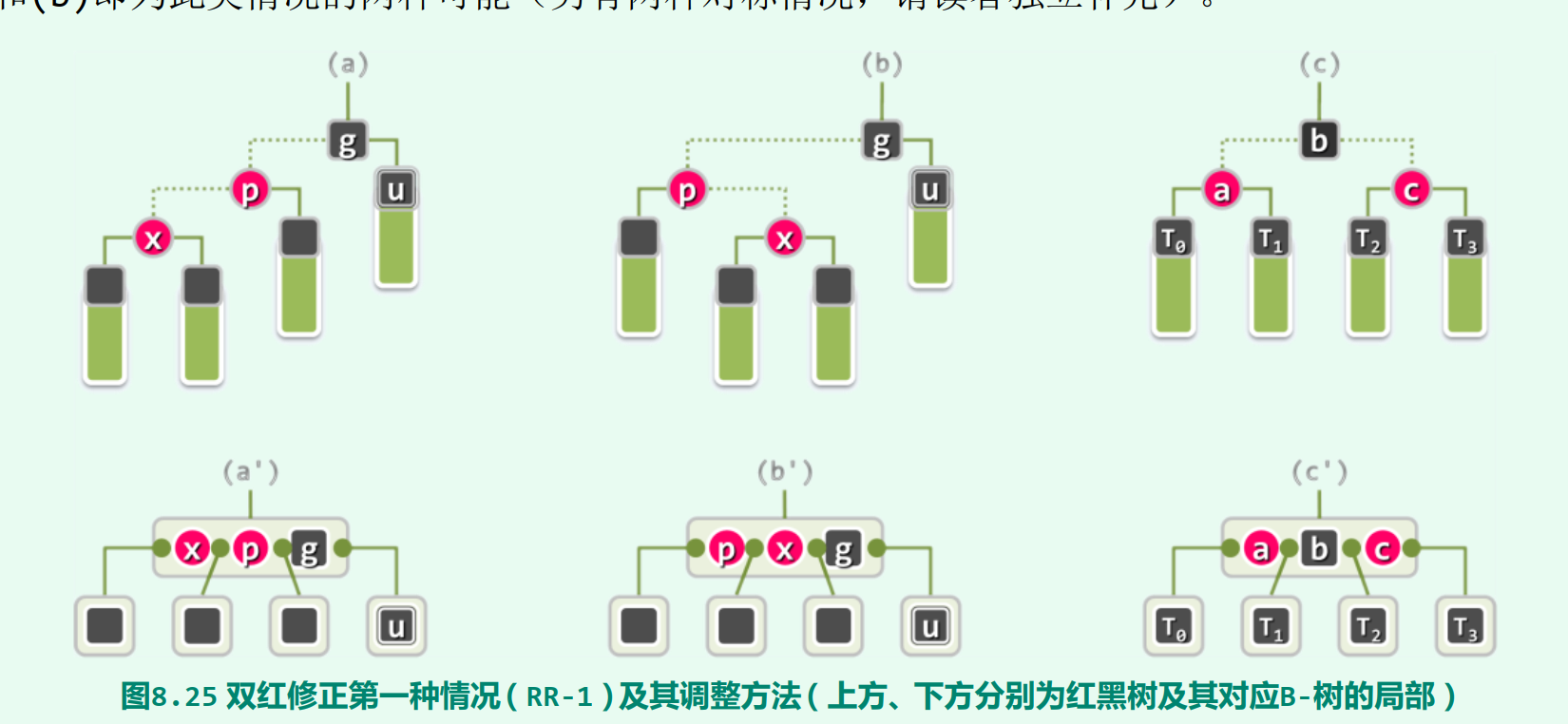
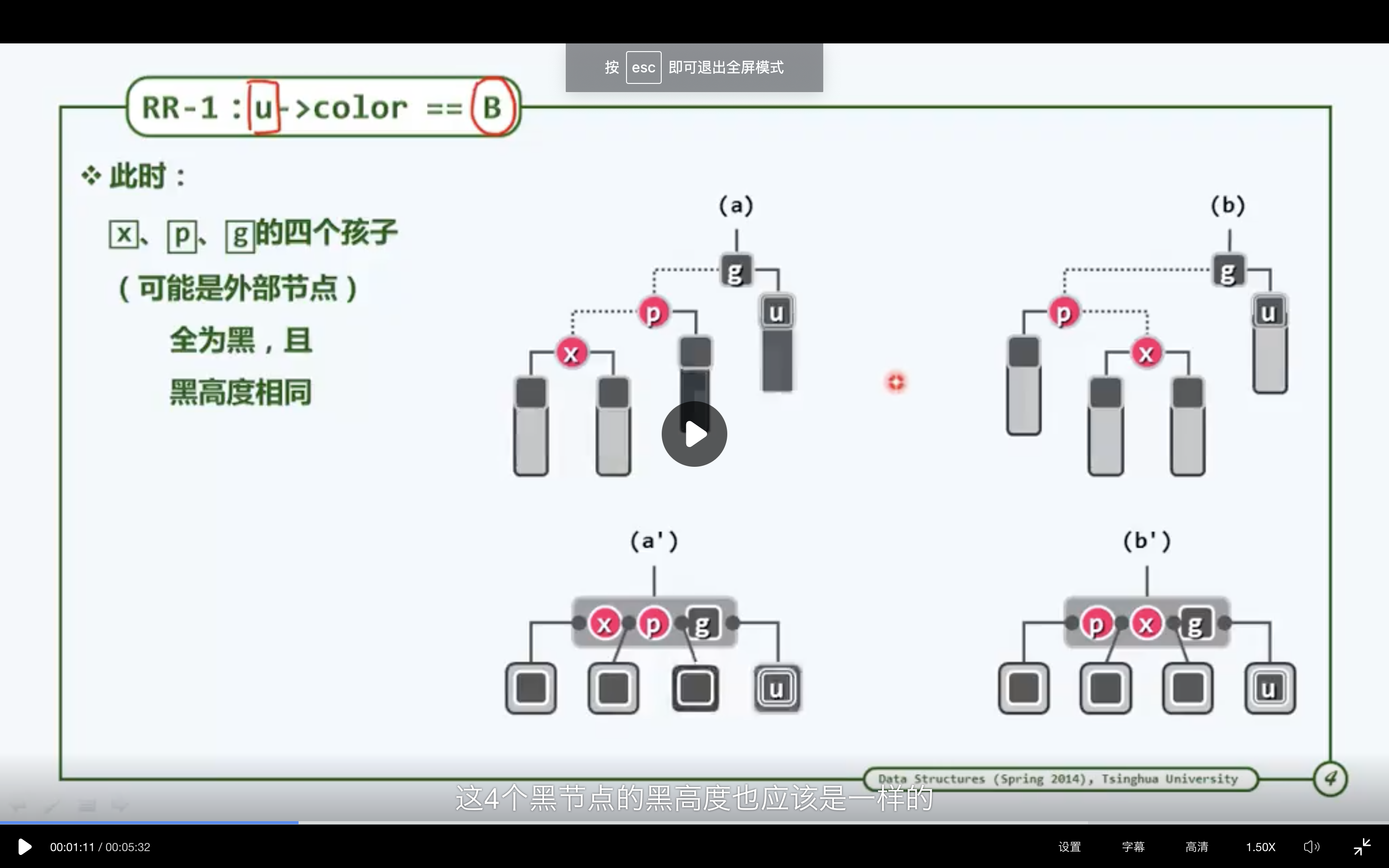
因新节点的引入,而导致父子节点同为红色的此类情况,称作“双红” (double red)。当前节点x的兄弟及两个孩子(初始时都是外部节点) ,始终均为黑色。
将x的父亲与祖父分别记作p和g。 既然此前的红黑树合法,故作为红节点p的父亲, g必然存
在且为黑色。 g作为内部节点, 其另一孩子(即p的兄弟、 x的叔父) 也必然存在, 将其记作u。以下,视节点u的颜色不同, 分两类情况分别处置。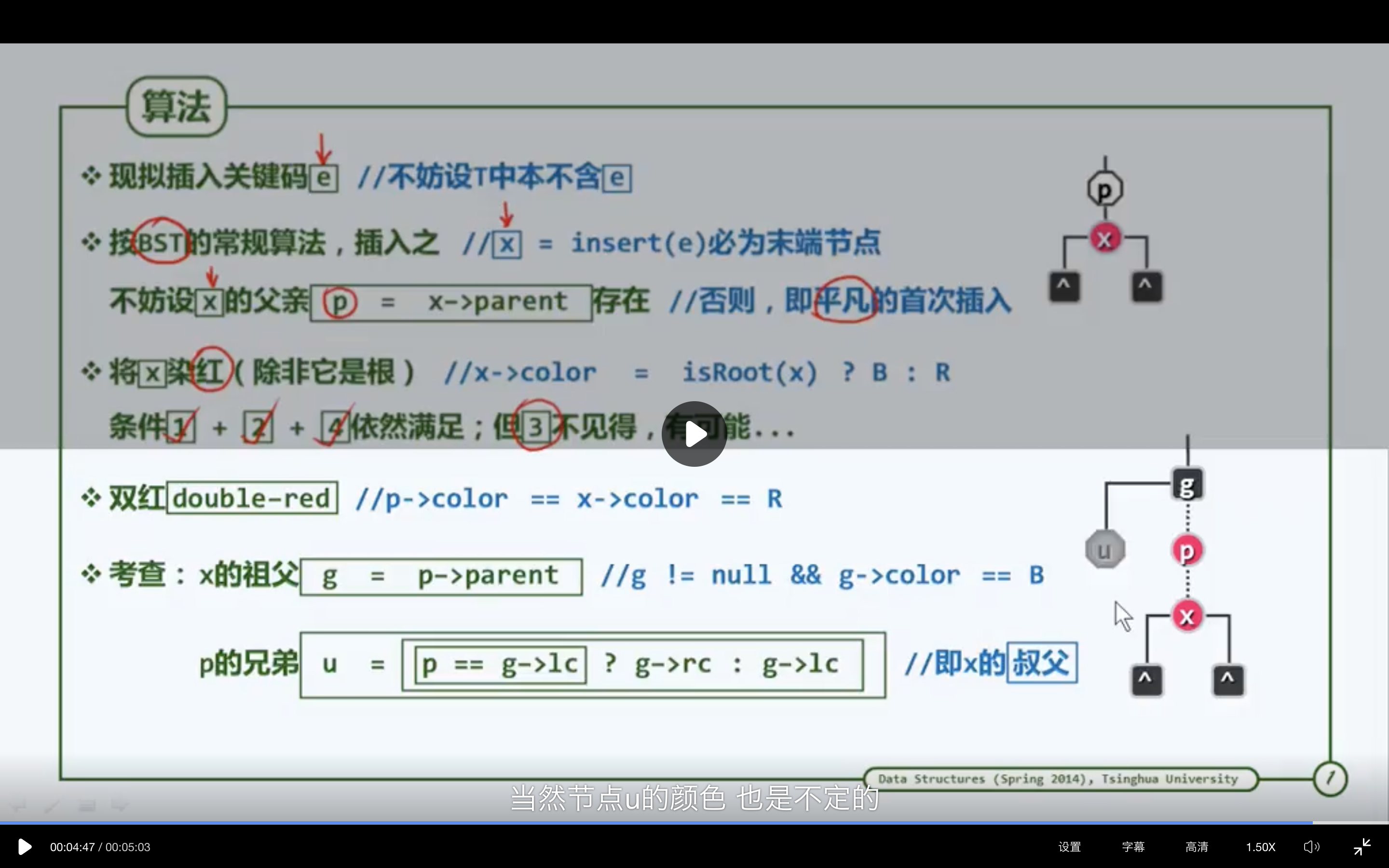
3.3.1 叔父节点u为黑节点的情况
3.3.2 叔父节点u为红节点的情况
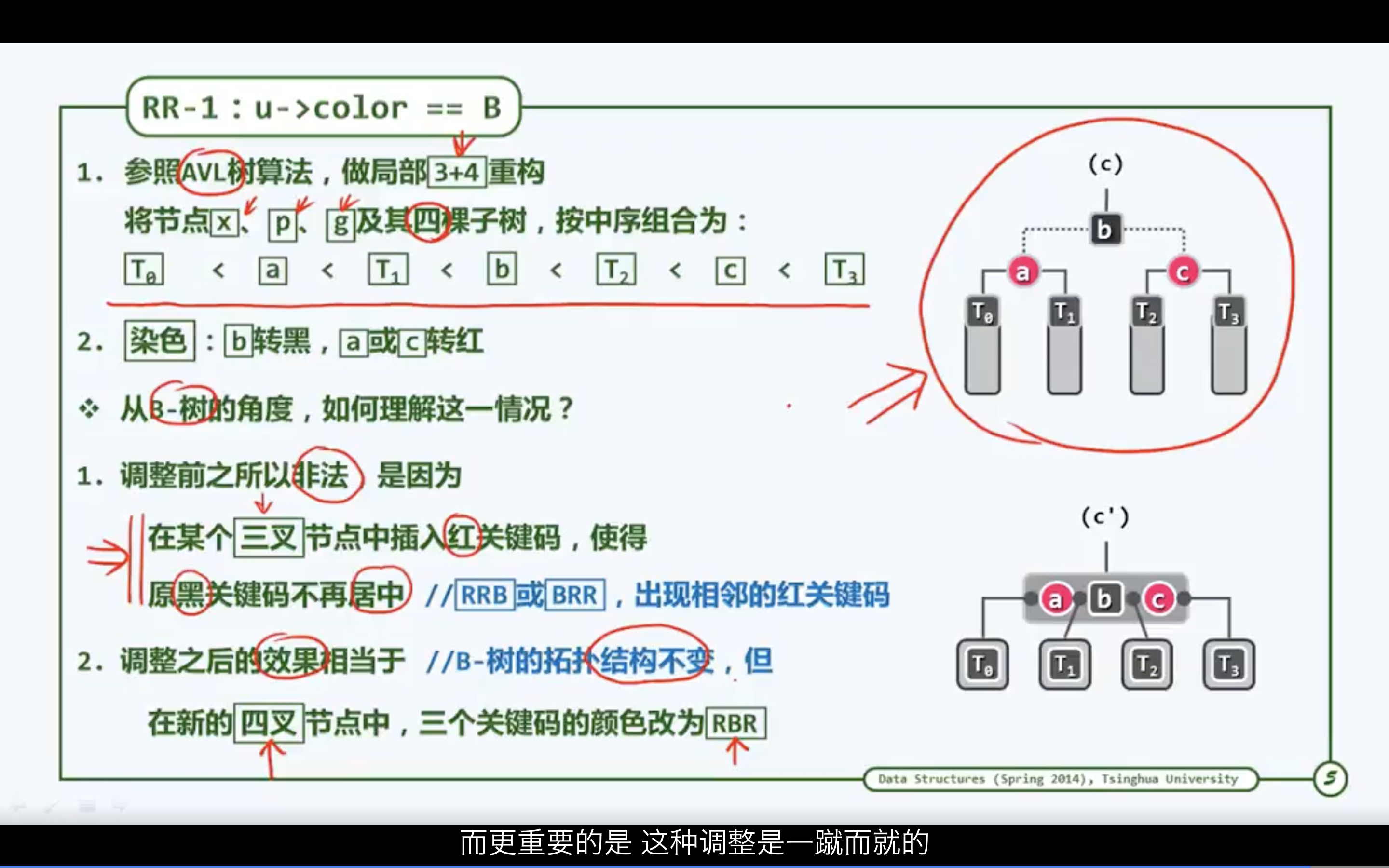
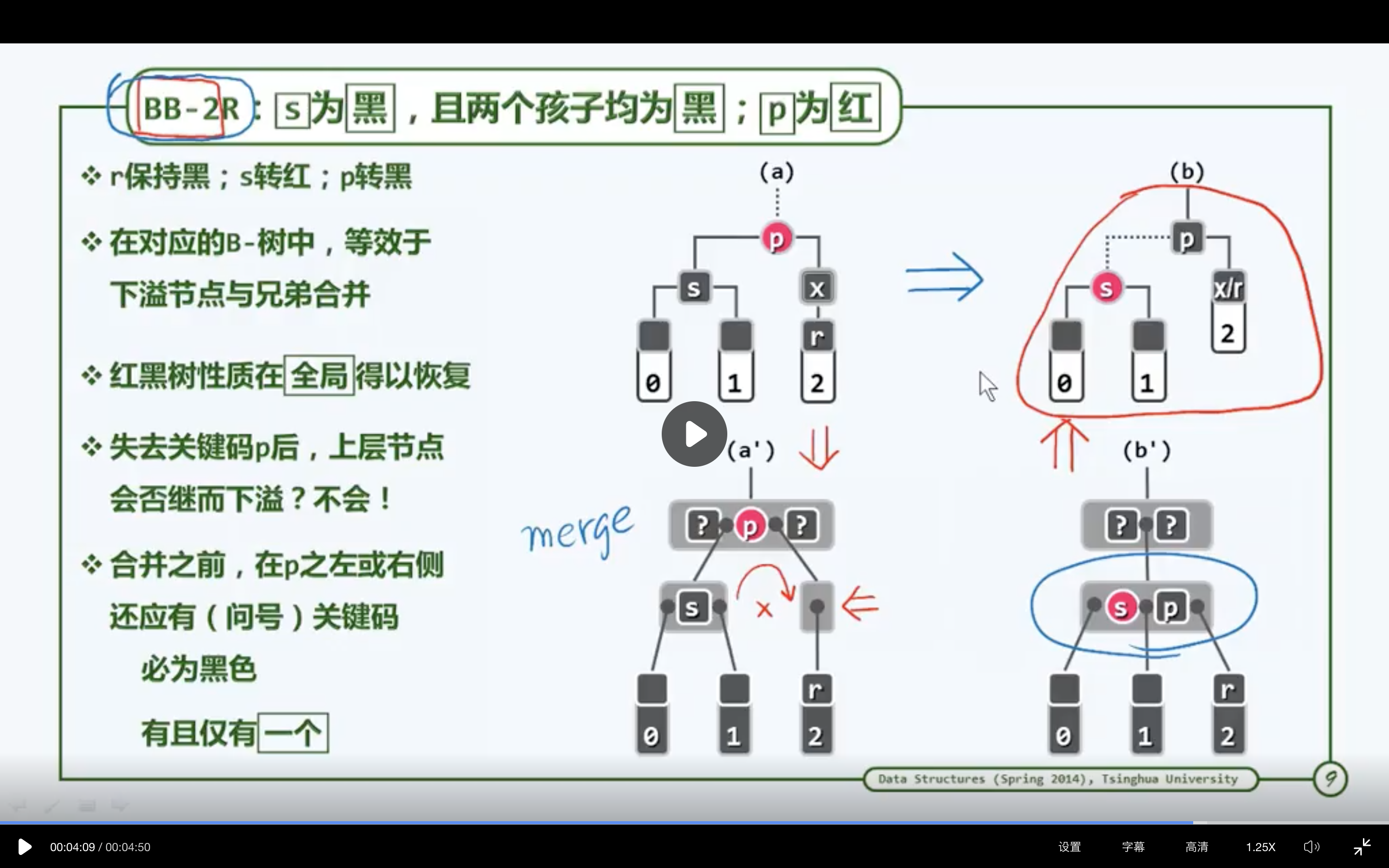
相当于在对应的B树中修复上溢缺陷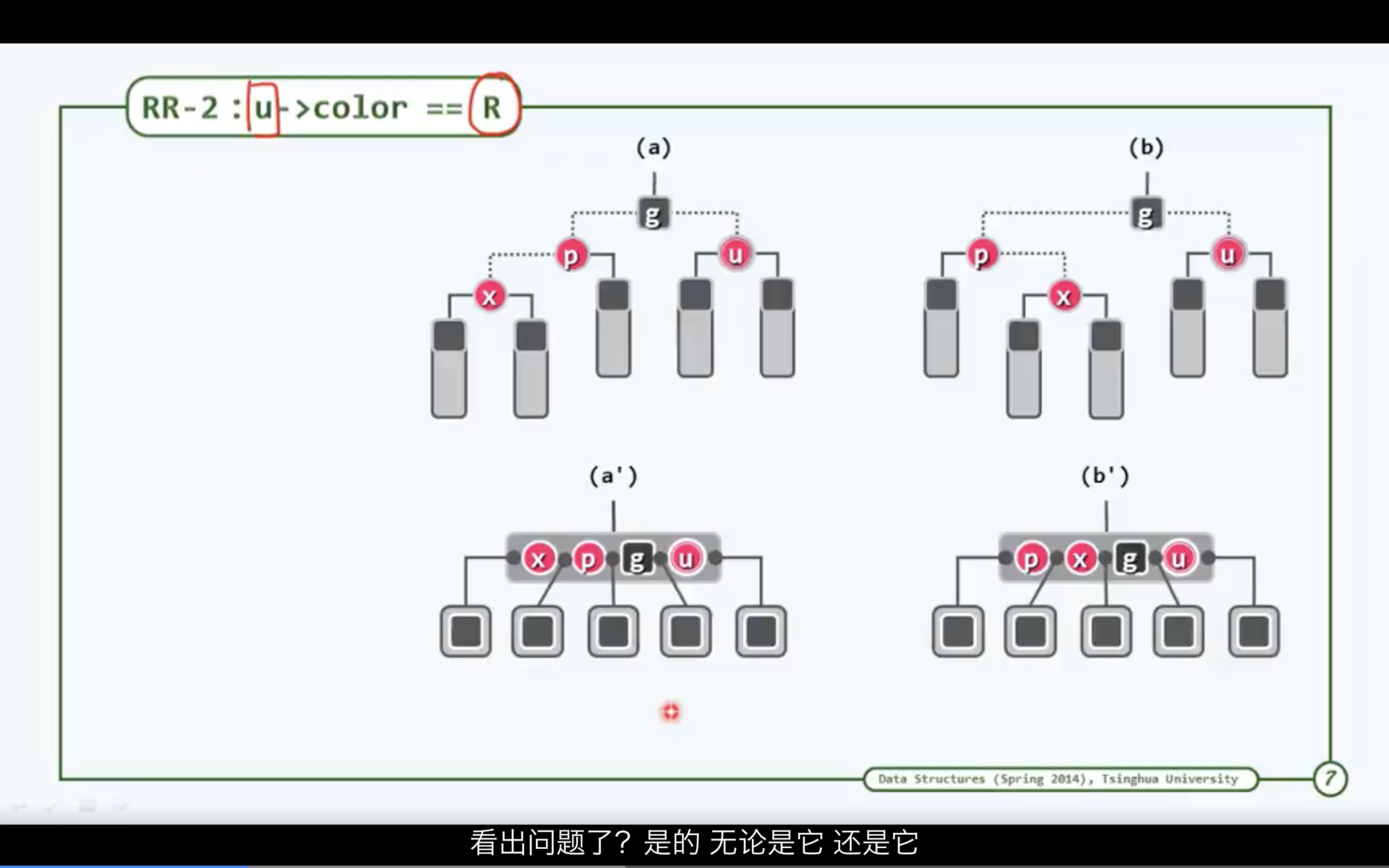
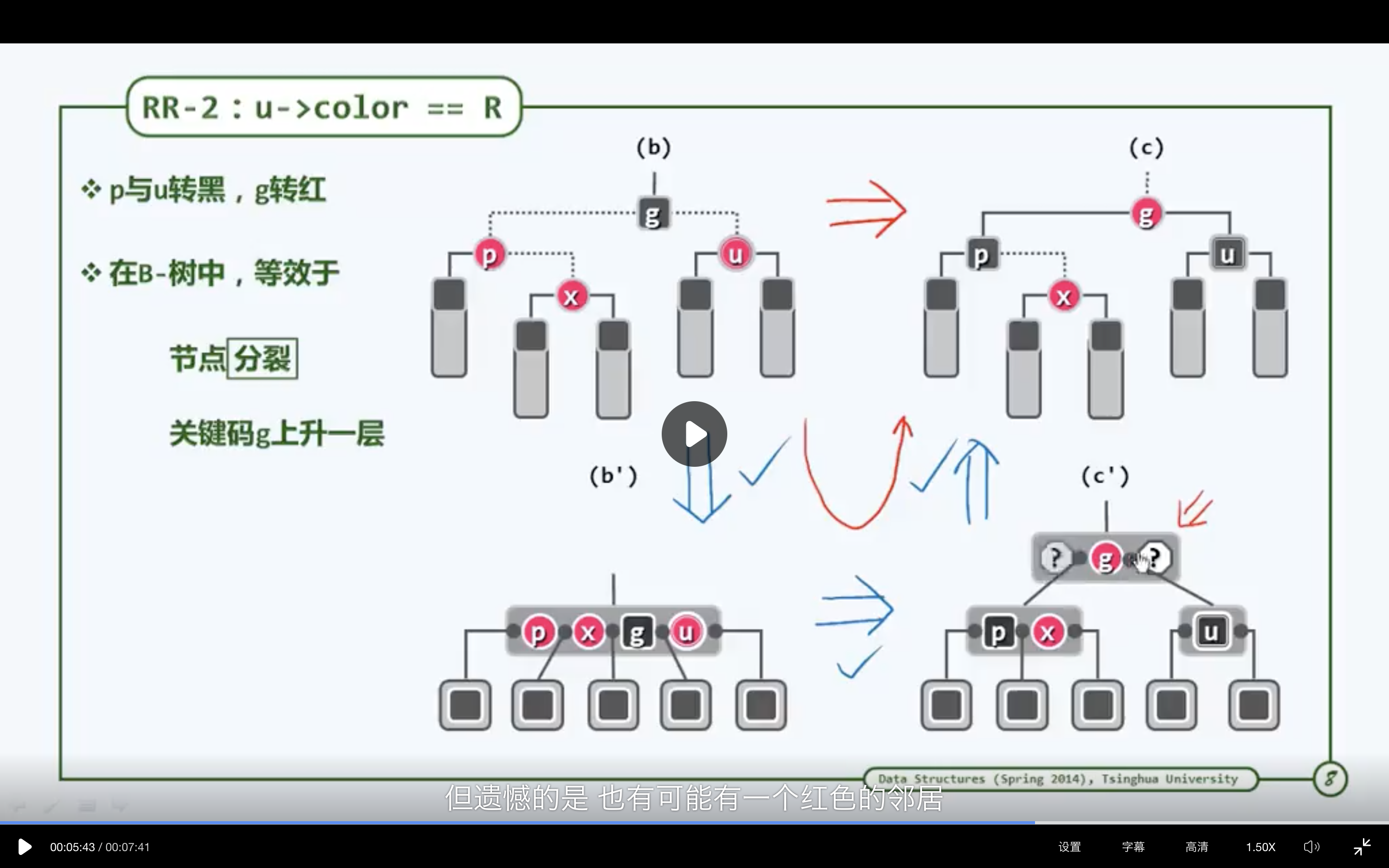
相当于在父节点插入一个新的关键码(红),在g的左侧或右侧至少应该拥有一个黑色的关键码,也有可能是一个红色的邻居。(相当于在g的父节点下新插入一个红色节点,也会发生双红缺陷)
3.4 删除
3.4.1 双黑缺陷
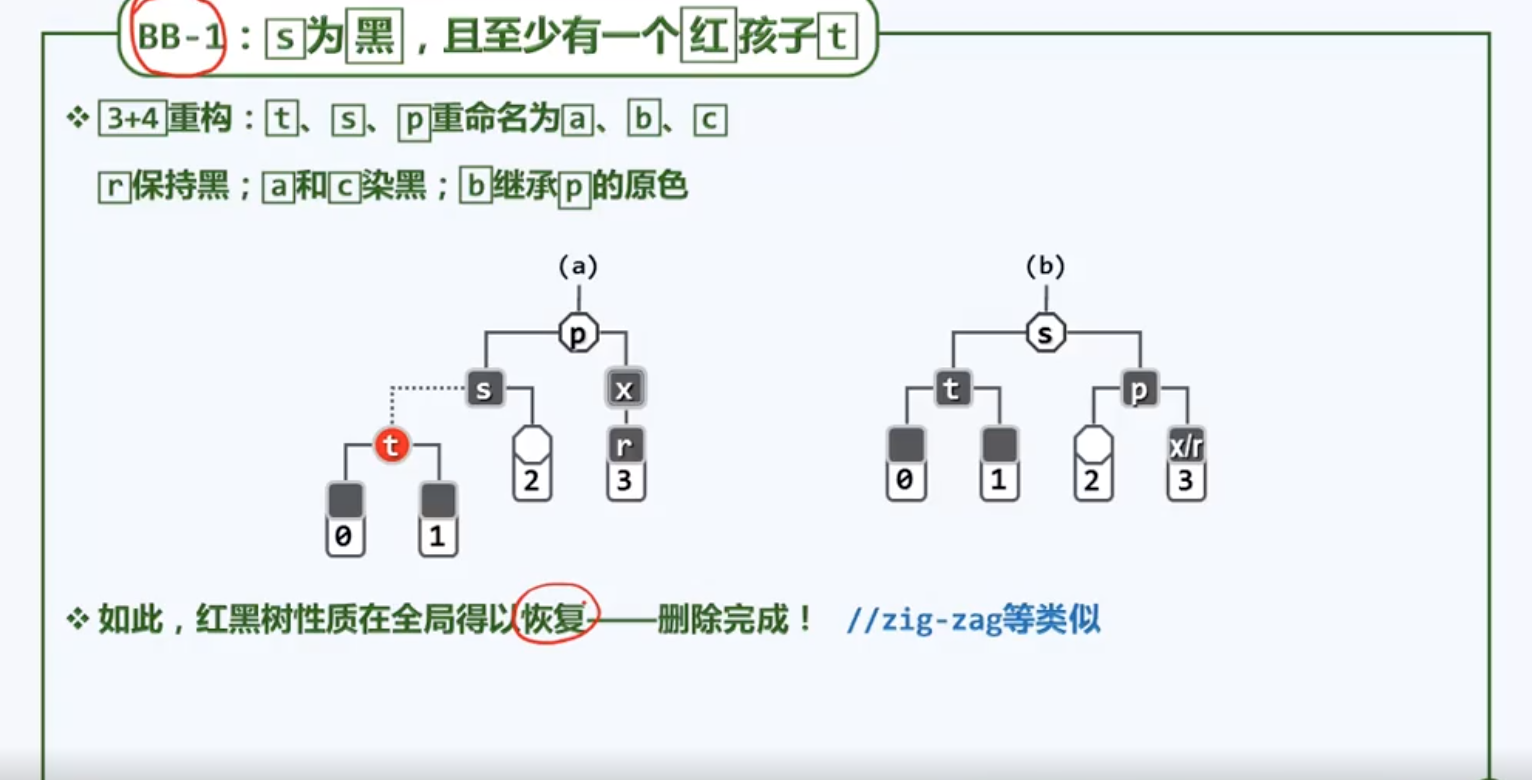
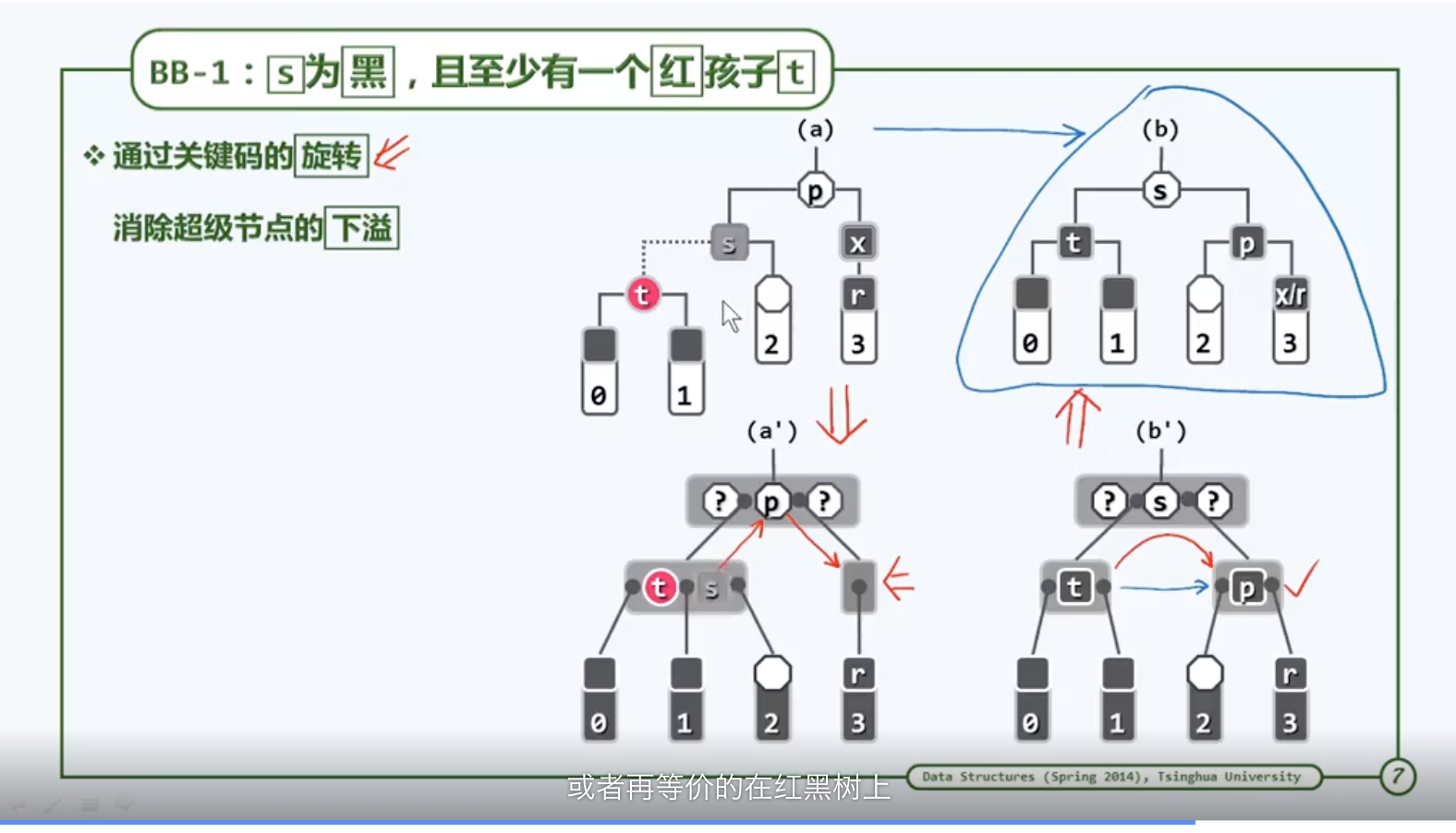
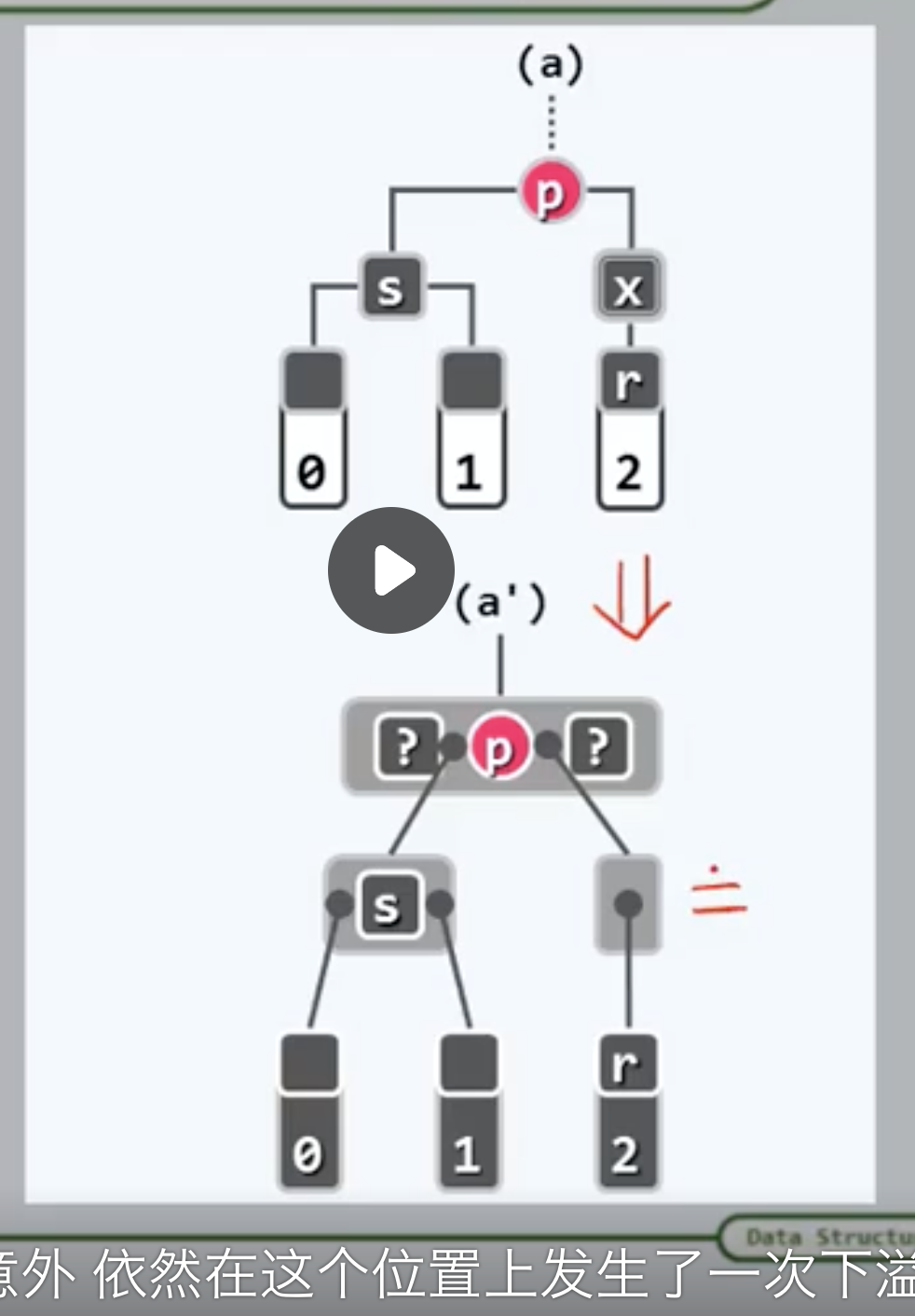
如果x和r都为黑色,在b树的角度来看。x独立成为一个超级节点,于是在唯一的一个关键码x删除后,这个超级节点也就自然发生下溢。在新树中需要考虑两个节点:首先是删除之后节点r的父亲p,还需要在原树中考察r的兄弟s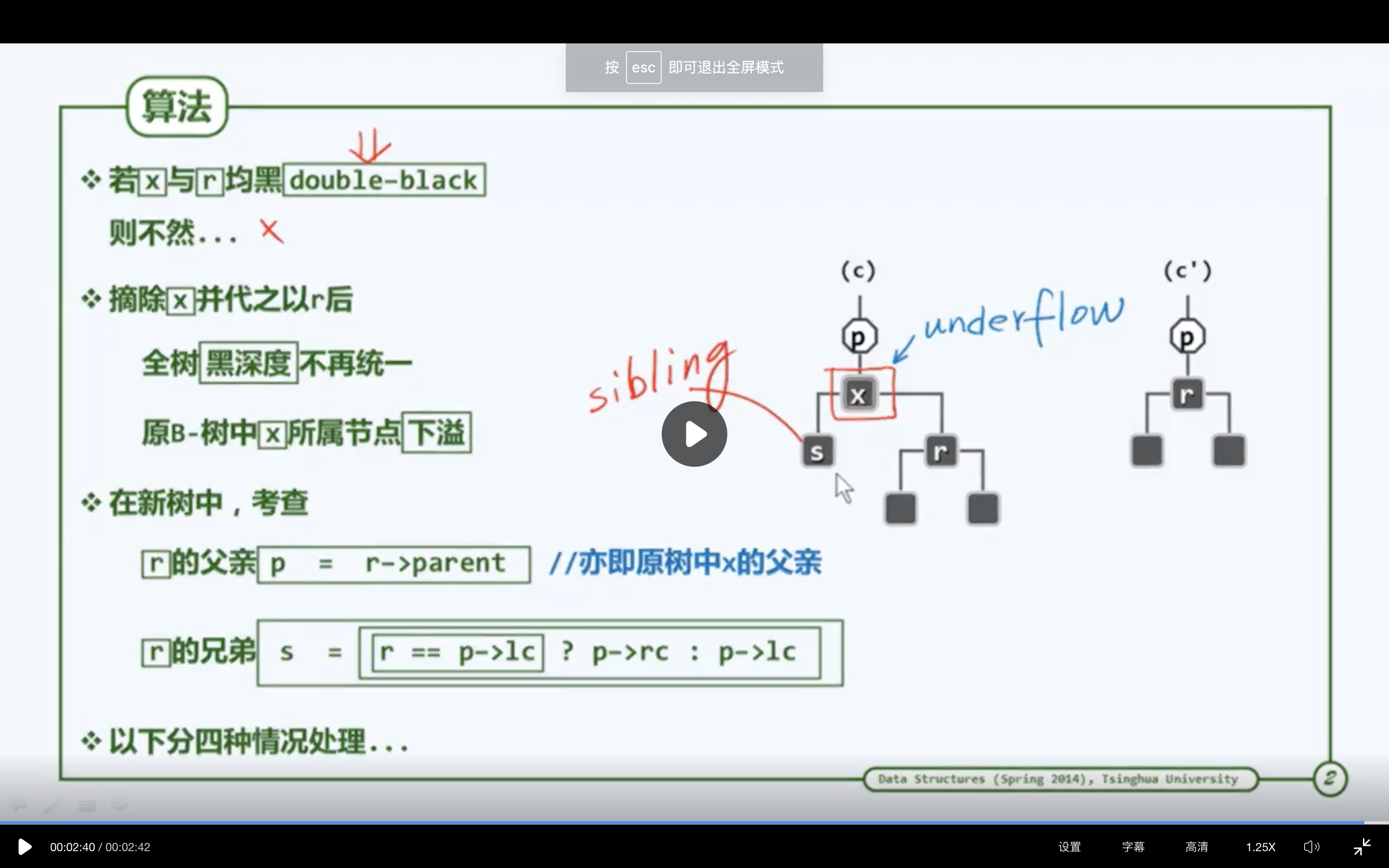
3.4.2 BB-1
3.4.3 BB-2R
3.4.4 BB-2B
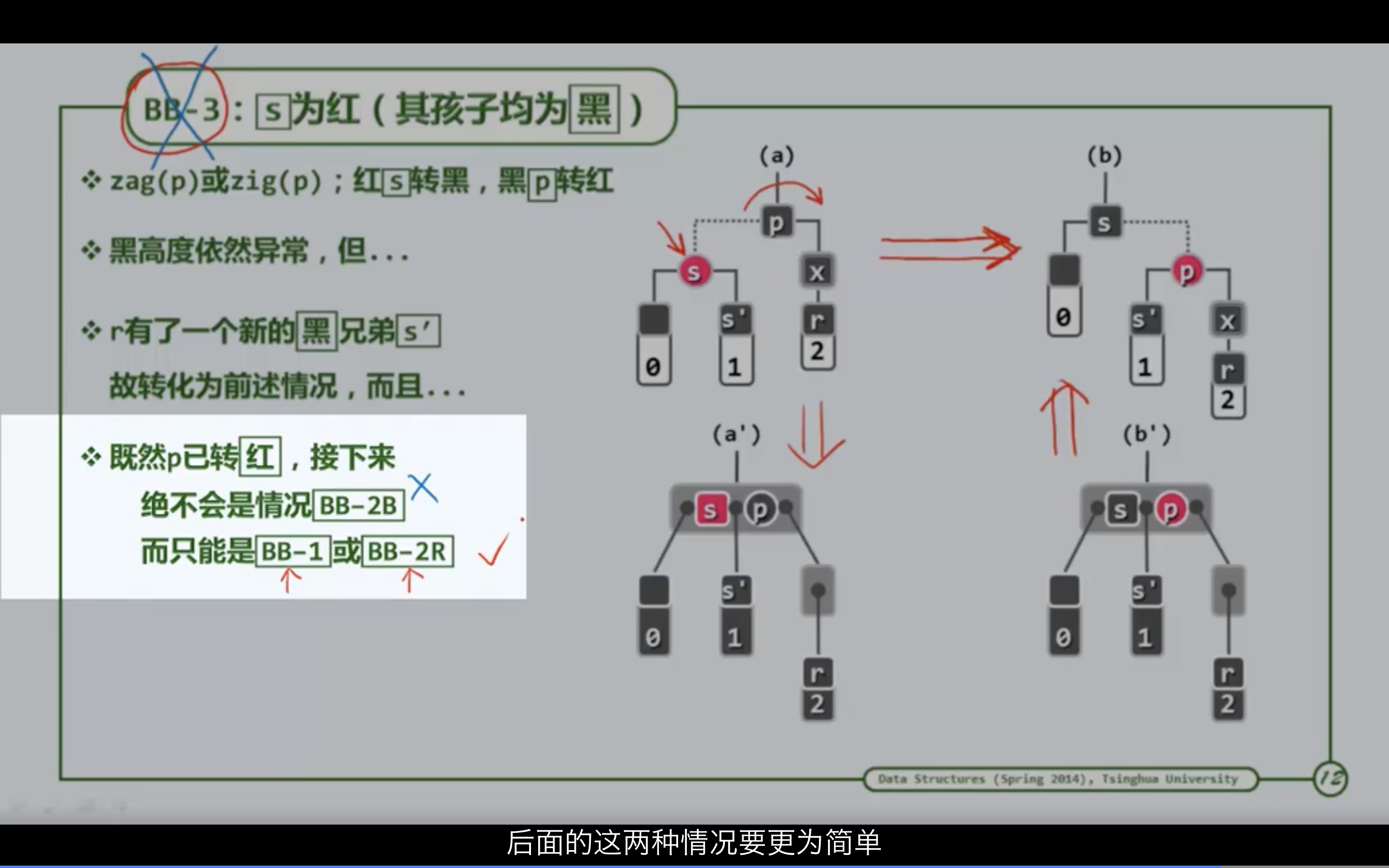
3.4.5 BB-3
兄弟节点s为红色的情况