RNN梯度消失-LSTM-GRU-SRU

LSTM 与 Gradient Vanish

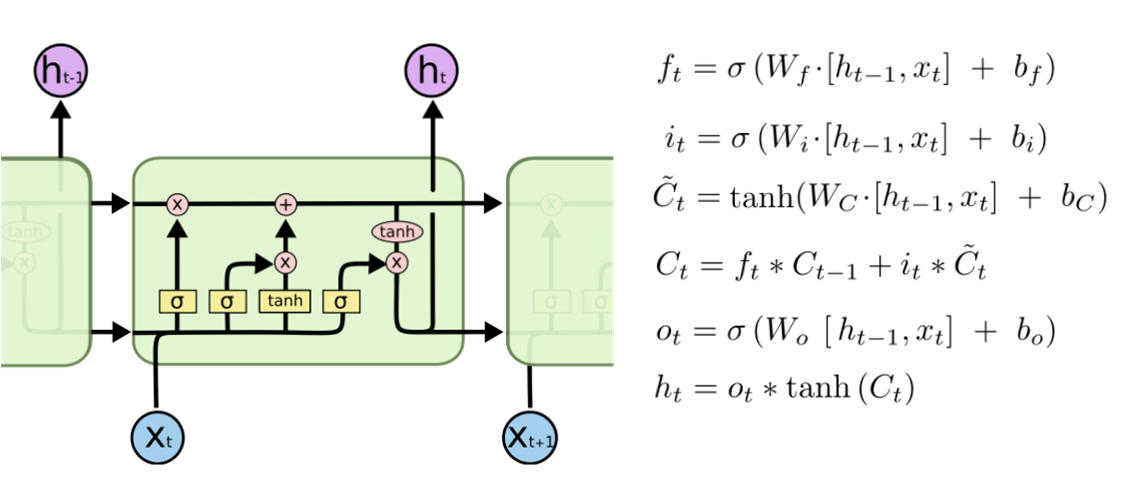
fig1. lstm 网络结构

• 第 4 个式子：遗忘门控制保留多少 C_t-1, 输入门控制输入多少新的信息 x_t （可以看到这个式子在 GRU 中对应的就是更新门 z_t）

• 输出门控制输出信息，在 GRU 中并没有对应的这个门。在 GRU 中就只有一个 h_t 状态向量

LSTM 是为了解决 RNN 的 Gradient Vanish 的问题所提出的。关于 RNN 为什么会出现 Gradient Vanish，上面已经介绍的比较清楚了，本质原因就是因为矩阵高次幂导致的。下面简要解释一下为什么 LSTM 能有效避免 Gradient Vanish。

对于 LSTM，有如下公式

模仿 RNN，我们来计算 ，有

公式里其余的项不重要，这里就用省略号代替了。可以看出当 时，就算其余项很小，梯度仍然可以很好导到上一个时刻，此时即使层数较深也不会发生 Gradient Vanish 的问题；当 时，即上一时刻的信号不影响到当前时刻，则梯度也不会回传回去； 在这里也控制着梯度传导的衰减程度，与它 Forget Gate 的功能一致。

GRU 在 lstm 上面的改进

fig2. gru 网络结构

• 合并了 cell state 和 hidden state

• 组合了遗忘门和输入门到一个单独的“更新门”(z_t)

• 根据上面的式子进行分析：

  • z_t 叫做 “更新门”：z_t 会控制添加多少新的信息。从最后一个式子看，如果 z_t 越大的话，那么加进来的 x_t 会多一些，保留的 h_t-1 会少一些，但是 h_t-1 实际上还主要受到 r_t 的影响。

  • r_t 叫做 “重置门”：r_t 主要用来控制保留多少上一个时刻的信息，越大则保留得越多。从倒数第二个式子看，如果 r_t 越大的话，h_t-1 就会越多的加入到 h_t 中。

SRU

• 内态 c_t 仍然利用以前的状态 c_t-1 更新，但是在循环步骤中，已经不再依赖于 h_t-1 了。结果，循环单元中所有的矩阵乘法运算可以很轻易在任何维度和步骤中并行化。

• 

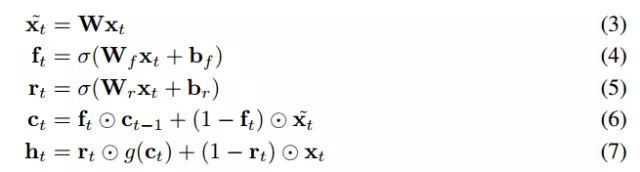
• 在上面的计算中，其中 ht 是先要计算 x_t, f_t, r_t, c_t；所以 h_t 的计算是最麻烦的，它依赖于其他的计算。在 lstm 中，c_t 的计算是依赖于 h_t-1 的，因此，在计算 h_t-1 计算完成之前，没有办法计算 c_t. 现在 SRU 中 c_t 的计算不再依赖 h_t-1 了，因此，计算完 c_t-1 之后，可以同时计算 h_t-1, c_t，不用等着 h_t-1 也计算完才往后计算(h_t-1的计算是比较麻烦的)。