一文搞懂HMM(隐马尔可夫模型)
隐马尔可夫模型是可用于序列标注问题的统计学习模型,描述由马尔科夫链随机生成观测序列的过程,是一种生成模型。
1 两个假设
- 齐次马尔科夫假设:马尔科夫性质,无记忆。就是当前时刻只受前一个时刻的影响,不会受更往前一些时刻的影响。
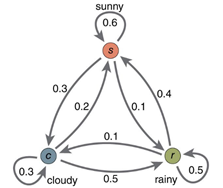
上图是一个马尔科夫链,每个节点表示状态,每条边表示转移概率。 在HMM中,假设状态有一个齐次马尔科夫链生成。(齐次:转移概率与起始位置无关)
- 独立输出假设:在 HMM 中,每个时刻会输出一个可见的符号,这个符号与该时刻的状态相关,而且至于该时刻的状态相关。
2 五个元素
通过上面的分析,就可以知道 HMM 模型其实是由五个元素构成的:状态序列I,输出序列O,转移概率分布A,输出概率分布B,初始状态概率分布π。
3 三个问题
概率计算问题
- 在已知模型 λ=(A,B,π)λ=(A,B,π) 和观测序列 O的情况下,计算 P(O|λ)P(O|λ) 的概率。
学习问题
- 已知观测序列O,估计模型λ=(A,B,π)λ=(A,B,π)的参数,使得 P(O|λ)P(O|λ) 最大。
预测问题(解码问题)
- 已知模型λ=(A,B,π)λ=(A,B,π)和观测序列O,预测最有可能的状态序列I.
4 以分词来理解预测问题
在自然语言处理中经常会用到隐马尔可夫模型,主要用在序列标注相关的问题上,比如:分词、命名实体识别和词性标注等。我自己也用BiLSTM + HMM 实现过简单的分词,在 HMM 中有 3 个问题,这是一个预测问题。
在分词中,可见序列指的是一个个文字,状态序列指的是该字的标注(词首,词中还是词尾等)。
已知:
A(状态转移概率矩阵,通过统计训练样本获得)
B(输出概率分布,以 Bi-LSTM 模型的分类输出概率作为对应时刻的输出概率)
π(初始状态概率分布,初始只能是 s 或者 b,取 Bi-LSTM 预测的第一个时刻的结果中 s 和 b 的概率值)
要求的是: 通过维特比译码求解最有可能的状态(标注)序列。
实际步骤是:
我们有4个类别(s:singleword, b:begin, m:middle, e:end),然后对于每一个字都有对应的类别,通过有监督学习的方法来学习。
(1)使用 Bi-LSTM 进行分类,获得每个字属于每个类别的概率;
(2)以每个字在LSTM的分类概率作为该时刻的输出概率 b_t(i);
(3)使用维特比译码获取最有可能的标注结果。
在传统方法中,输出概率分布也是通过统计的方式来计算的。而在这里,我们先用 Bi-LSTM 分类的方式计算输出,然后再用维特比译码来进行强矫正。

