不同激活函数及其优缺点

参考1：【机器学习】神经网络-激活函数-面面观(Activation Function) 参考2：深度学习中激活函数的优缺点

为什么要引入激活函数？
引入非线性激活函数，神经网络财局比了分层的非线性映射能力。

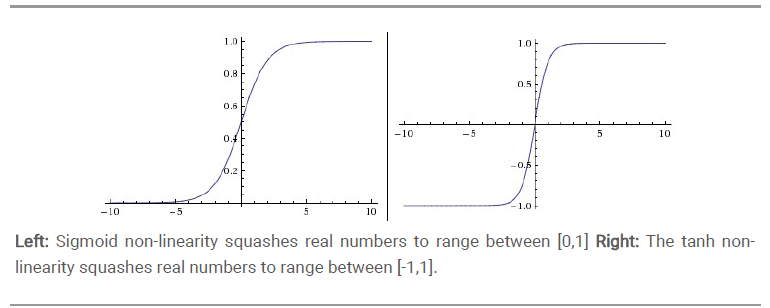
sigmoid

• 

• 好处

  • 是在物理意义上最为接近生物神经元。 (0, 1) 的输出还可以被表示作概率，或用于输入的归一化。Batch Normalization的逐层归一化，Xavier和MSRA权重初始化等代表性技术。能够一定程度上面缓解梯度消失的问题。

• 缺点

  • 梯度消失：sigmoid 在定义域内处处可导，且两侧导数逐渐趋近于0。因此一旦输入落入饱和区，f’(x) 就会变得接近于0，导致了向底层传递的梯度也变得非常小。此时，网络参数很难得到有效训练。这种现象被称为梯度消失。

  • 非零均值：这会导致后层的神经元的输入是非0均值的信号，这会对梯度产生影响。以 f=sigmoid(wx+b)为例， 假设输入均为正数（或负数），那么对w的导数总是正数（或负数），这样在反向传播过程中要么都往正方向更新，要么都往负方向更新，导致有一种捆绑效果，使得收敛缓慢。

  • 激活函数计算量大（指数运算），反向传播求误差梯度时，求导涉及除法

tanh

• 

• 零均值化

relu

• 

• 好处

  • 计算复杂度低，不需要进行指数运算

  • 梯度不会饱和，解决了梯度消失问题，SGD算法的收敛速度要比 sigmoid 和 tanh 快

  • 保留正向激活的特征，防止过拟合（这也是缺点）

• 缺点

  • 非零均值化

  • 不会对数据做幅度压缩，因此数据的幅度会随着模型层数的增加而不断扩张

  • Dead ReLu Problem，部分神经元坏死。某些神经元永远不会被激活，导致相应参数永远不会被更新（在负数部分，梯度为0）。

    • 产生这种现象的两个原因：参数初始化问题；learning rate太高导致在训练过程中参数更新太大。

    • 解决方法：采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。