先验-后验-似然-贝叶斯

似然 先验

后验 事实

对于参数估计，主要分为两种学派两种观点：

• 频率学派通过优化准则，如最大化似然函数来选择参数：

• 贝叶斯学派则假定参数服从一个先验分布 p(θ)，由贝叶斯推断来计算后验分布：

后验分布 = 似然函数 * 先验分布

最大似然估计和最大后验概率估计

参考1：详解最大似然估计（MLE）、最大后验概率估计（MAP），以及贝叶斯公式的理解

• 似然函数

  • 指的是在固定参数 θ 的情况下，事实发生的概率 p(x|θ) 是多少。最大似然估计要做的就是我们找到一个合理的参数 θ，使得最终的发生概率最大（令 p(x|θ) 取得最大值）。

  • 但是，在最大似然估计中，假定参数 θ 的取值是随机的。但是事实中，这些参数往往不是完全随机的，而是也服从一个概率分布，这就是先验概率，它指的是参数的先验分布，注意，是参数的分布。

• 后验概率

  • 实际上就是在似然函数的基础上面，加上了参数的先验概率分布。

• 具体的例子可以参考1上面链接中的抛硬币例子，讲得听通俗易懂的。

这两种参数估计方式都是非常简单的，在实际问题中，p(x|θ) 一般都是有具体的概率计算公式，其中 x 都是已知的（训练数据）比如神经网络中可能就是最后一层某个节点的输出值，有了这个计算公式之后，我们要做的最大似然估计实际上就是在最大化这个公式。
同理，最大后验概率估计也是解一个最大化问题，只不过他的计算公式中多了先验分布这一项。

参考2：贝叶斯思想以及与最大似然估计、最大后验估计的区别

• ML估计不会把先验知识考虑进去，而且很容易造成过拟合现象。

  • 举个例子，比如对癌症的估计，一个医生一天可能接到了100名患者，但最终被诊断出癌症的患者为5个人，在ML估计的模式下我们得到的得到癌症的概率为0.05。

• MAP与ML最大的不同在于p(参数)项，所以可以说MAP是正好可以解决ML缺乏先验知识的缺点，将先验知识加入后，优化损失函数。

• 其实p(参数)项正好起到了正则化的作用。如：如果假设p(参数)服从高斯分布，则相当于加了一个L2 norm；如果假设p(参数)服从拉普拉斯分布，则相当于加了一个L1 norm。（推导过程见：【机器学习】贝叶斯角度看L1，L2正则化）

logistic 交叉熵损失函数

参考3：（译）神经网络基础（1）：Logistic 回归

上面介绍了 ML 和 MAP 两种参数估计方法，他们最终都是为了解决一个最大化问题。在实际工程实现中，一般都是先取负对数概率函数然后再求解最小化。因为取对数之后和原问题还是等价的，接着去负号把最大化问题转为最小化，这样子会比原问题更好求解。

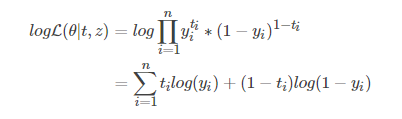
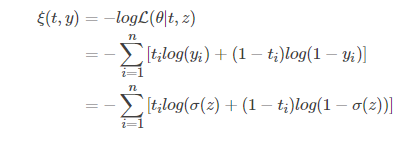
在 logistic 中，我们最开始求解的是最大似然估计问题，然后经过一系列的等价变换（-log）最后得到的交叉熵，从信息论的角度来说，交叉熵和 KL 散度是等价的。