LDA主题模型

请介绍一些 LDA 模型的基本原理？

参考： 文档主题生成模型（LDA）

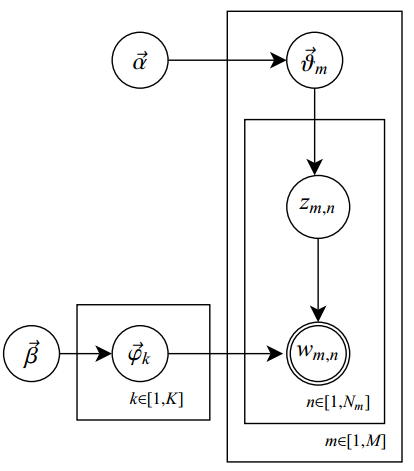
总的来说，LDA 主题模型是一种无监督的学习方法，模型最终输出每个文档的主题分布。
实际中，我们根据语料的数量和分布来设定一个主题数目，比如我们现在有200万个文档，选择200个主题进行学习。lda的主题叫做隐主题，意思就是说这些主题都是隐藏的，我们并不知道这200个主题最后具体指的是什么内容，当模型训练完成的时候，每个主题实际上就是一个词频分布。最终，每个文档的每个词都会被指定到某一个具体的主题中，这样子我们就可以得到这个文档的主题分布。

现在有一个 LDA 模型，我们假定取了 200 个主题，对于一个长度为 1000 词的文章 [w1, w2, …, w1000]，LDA模型假设这个文章是通过下面的步骤生成的：

• 先从主题分布中抽取出一个主题

• 在上面抽取出来的主题所对应的词分布中抽取一个词

• 然后不断的重复，直到生成这 1000 个词

统计文本建模的目的其实很简单：就是估算一组参数，这组参数使得整个语料库出现的概率最大。这是很简单的极大似然的思想了，就是认为观测到的样本的概率是最大的。** **建模的目标也是这样，下面就用数学来表示吧。
一开始来说，先要注意假设了一些隐变量z，也就是topic。每个文档都符合一个topic的分布，另外是每个topic里面的词也是符合一个分布的，这个似然是以文档为单位的。极大似然式子全部写出来是下面的样子的

其中的M表示文档个数。其中的α，就是每个文档符合的那个topic分布的参数，注意这个家伙是一个向量，后面会再描述；其中的β，就是每个topic里面的词符合的那个分布的参数，注意这个也是一个向量。

在LDA中，实际上我们要解的就是一个最大似然问题：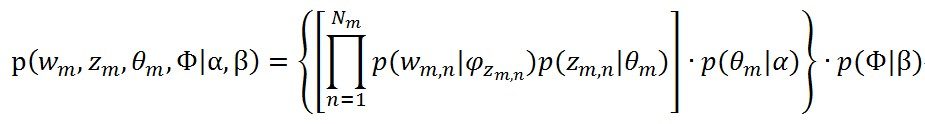

但是这个公式中包含的隐变量非常多，没有办法直接求解。Gibbs Sample 方法就是用来解决这个问题，经过一系列的推导之后得到完全条件分布的公式：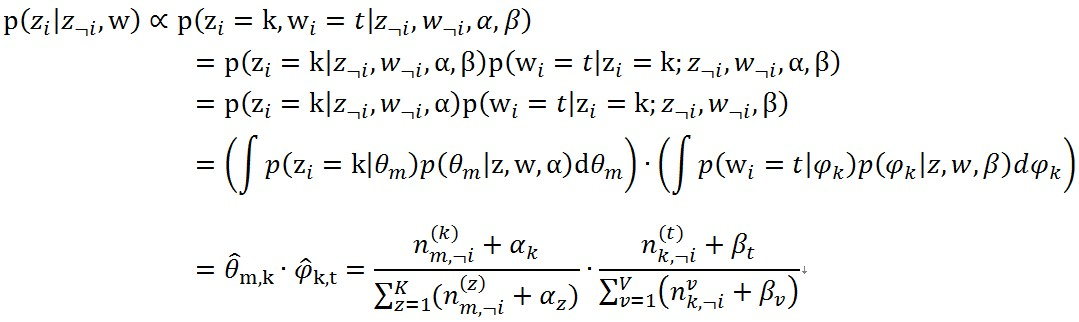

在实际的工程计算中，我们也就是通过这样的一个计算公式就够了。通过这个公式，我们就能够计算出文档中每个词属于各个主题的概率，从而通过多项分布采样就可以确定每个词的所属主题。具体的计算过程如下：

• 多项分布采样

public int sampleTopic(double p[]) {
        // 多项式采样
        // 计算主题的累积概率
        for (int k = 1; k < K; k++) {
            p[k] += p[k - 1];
        }
        // 归一化
        double u = Math.random() * p[K - 1];
        int topic = -1;
        for (topic = 0; topic < K; topic++) {
            if (p[topic] > u)
                break;
        }
        return topic;
    }

LDA相关的知识点

参考：随机采样和随机模拟：吉布斯采样Gibbs Sampling

• 平稳马尔科夫链：马尔科夫链定义本身比较简单，它假设某一时刻状态转移的概率只依赖于它的前一个状态。马尔科夫链模型的状态转移矩阵收敛到的稳定概率分布与我们的初始状态概率分布无关。

• 马尔科夫链采样：for t=0 to n1+n2−1，从条件概率分布P(x|x)中采样得到样本 x

• MCMC：Markov链通过转移概率矩阵可以收敛到稳定的概率分布。这意味着MCMC可以借助Markov链的平稳分布特性模拟高维概率分布；当Markov链经过burn-in阶段，消除初始参数的影响，到达平稳状态后，每一次状态转移都可以生成待模拟分布的一个样本。而Gibbs抽样是MCMC的一个特例，它交替的固定某一维度，然后通过其他维度的值来抽样该维度的值，注意，gibbs采样只对z是高维（2维以上）（Gibbs sampling is applicable in situations where Z has at least two dimensions）情况有效。

• 在 lda 中，我们要预测每个词的主题，先把这篇文章中其他的词固定，然后就可以计算到这个词的一个概率分布。然后再根据这个分布来采样得到这个词的主题。接下来，我们固定这个词，继续对下一个词的主题进行采样…如此迭代，最后达到收敛。如上图中，我们要计算某个词属于主题k的概率，当我们固定这个文档中其他每个词的主题时，上述的这个公式中每个值都能够确定下来。

怎么来进行主题数量的选择？

• 数据量

• 数据分布，我们的资讯数据量挺大的，但是主要是理财、金融相关的，所以话题数量并不需要非常多。

• 通过困惑度等一些指标来评判

• 其实话题一般不是很多，也可以肉眼看看效果呀

困惑度

通俗来说，困惑度可以理解为：对于一篇文章，我们的LDA模型有多不确定它是属于某个topic的。topic越多，Perplexity越小，但是越容易overfitting。

相似度

相似度主要衡量 lda 得到的各个主题之间的相似程度，当各个topic之间的相似度的最小的时候，就可以算是找到了合适的topic个数。