SymPy 是一个由 Python 语言编写的符号计算库。我将在本文中简要地介绍如何利用 SymPy 进行符号计算。在介绍 SymPy 之前，我们首先要明确何谓符号计算？计算机代数系统又是什么？

什么是符号计算 ？

处理数学对象的计算称为符号计算。在符号计算中，数学对象是精确表示的，而不是近似的，未计算的数学表达式会以符号形式保留。与符号计算相对应的是数值计算，下面将以两个例子来展示二者之间的区别。

数值计算示例

下面是一个计算 数值解的例子：

import math
math.pi
print(math.sin(math.pi))

符号计算示例

下面是一个计算 解析解的例子：

from sympy import *
sin(pi)

对比 的数值和符号计算结果可以发现，数值计算结果无法精确地表示出 ，只能用一个很小的浮点数 表示，而符号计算结果则得出 。
明确了数值计算和符号计算之间的区别后，让我们再来认识什么是计算机代数系统。

什么是计算机代数系统 ？

计算机代数系统（Computer Algebra System，缩写作：CAS）是进行符号运算的软件。在计算机代数系统中运算的对象是数学表达式，通常表达式有如下几类：

• 多元多项式
• 标准函数（三角函数、指数函数等）
• 特殊函数（ 函数、Bessel 函数等）
• 多种函数组成的复合函数
• 表达式的导数、积分、和与积等
• 级数
• 矩阵

以下列出了几种典型的符号计算：

• 表达式化简
• 表达式求值
• 表达式的变形：展开、积、幂、部分分式表示、将三角函数转换为指数函数等
• 一元或多元微分
• 带条件的化简
• 部分或完整的因式分解
• 求解线性或非线性方程
• 求解微分方程或差分方程
• 求极限
• 求函数的定积分、不定积分
• 泰勒展开、洛朗展开等
• 无穷级数展开
• 级数求和
• 矩阵运算
• 数学公式的 或 显示

通常符号计算软件也具备一定的数值运算能力，例如可以进行如下运算：

• 求函数确切值
• 求高精度值，如
• 线性代数的数值运算

此外符号计算软件也具有描绘二维、三维函数图像的功能。
实际上，目前存在众多的计算机代数系统，下面列出了几种：

• Maple
• MuPAD
• Maxima
• Mathcad
• Mathematica
• MATLAB Symbolic Math Toolbox
• SageMath

  为什么选择 SymPy ？

  那么，是什么让 SymPy 从这众多软件中脱颖而出，让我们选择它呢？我觉得有如下 4 个原因：

1. SymPy 是自由软件，免费开源，在遵守许可证条款的前提下，用户可以自由地根据自己的需求修改其源代码。与之形成对比的是，Maple、MuPad、Mathcad、MATLAB、Mathematica 等都是商业软件，价格昂贵；
2. SymPy 使用 Python 编写而成，与使用自己发明的语言的计算机代数系统相比（如 Maxima 由 LISP 编写)，SymPy 具有很强的通用性。SymPy 完全用 Python 编写，完全在 Python 中执行。这样，只要您熟悉 Python，那么 SymPy 将会很容易入门；
3. 与另一个使用 Python 的符号计算软件——SageMath 相比，SymPy 的优点是安装包体积小；
4. SymPy 的一个重要特性是，它可以作为库集成到其他软件中，为别的软件所用。SageMath 便是将 SymPy 作为其子模块，然后再加入其他模块，构建出一个功能齐全的数学软件。

   准备知识

   在学习如何使用 SymPy 进行符号计算之前，请确保您满足如下几个条件：

• 学习过微积分
• 学习过线性代数
• 熟悉 Python 基本语法
• 了解 Python 面向对象编程方法
• 会使用 JupyterLab Notebook 交互式开发环境
• 了解 是什么东西

  如何使用 SymPy ？

  前面的第 1 个符号计算示例展示了如何利用 SymPy 精确地计算三角函数，实际上，它的功能远不仅于此。作为一个强大的符号计算库，它几乎能够计算所有带符号变量的表达式。下面从本节开始将介绍如何使用 SymPy。

  导入 SymPy 库

  在使用 SymPy 之前需要先将其导入，有两种方式：

1. 直接导入：

   import sympy

2. 利用 from 语句导入：

   from sympy import *

   两种方式都导入了 SymPy 库中的所有函数、对象、变量等。区别是调用方式不同。比如在调用 sqrt( )函数时，前者应写成 sympy.sqrt(2)，后者则直接写成 sqrt(2)。为了力求简洁，我们使用第 2 种方式导入 SymPy 。

   注意：为了防止命名空间冲突，PEP 标准推荐使用第一种方式导入库。但是，通常一个符号运算 Python 源文件是单独使用的，稍加注意就可以避免命名空间冲突的问题。

   新建符号

   在使用符号之前，先要利用 symbols 函数定义符号，语句是：

   # 新建符号 x, y
   x, y = symbols('x y')

   还有一个更简洁的方法是，利用 SymPy 的 abc 子模块导入所有拉丁、希腊字母：

   # 利用 SymPy 的 abc 子模块新建符号 x, y
   from sympy.abc import x, y

   注意：希腊字母 > (lambda) 是 Python 保留关键字，当用户需要使用这个字母时，请写成 > lamda(不写中间的 ‘b’)。 新建符号变量时可以指定其定义域，比如指定 :

   x = symbols('x', positive = True)

   这样在求解过程中 必须满足这个前提条件。
   可以利用 symbols 函数依次新建类似 的多个变量：

   vars = symbols('x_1:5')
   vars
   (x_1, x_2, x_3, x_4)
   vars[0]

   
   下面是一个符号计算的完整例子：

   from sympy import *
   x, y, z = symbols('x y z')
   y = expand((x + 1)**2) # expand() 是展开函数
   y

   

   z = Rational(1, 2) # 构造分数 1/2
   z

   

   符号计算基本操作

   在本节中，我将介绍几个符号计算的基本操作。

   替换

   采用符号变量的 subs 方法进行替换操作，例如：

   x = symbols('x')
   expr = cos(x) + 1
   expr.subs(x, 0)

   

   将字符串转换为 SymPy 表达式

   利用 sympify 函数可以将字符串表达式转换为 SymPy 表达式。 注意：> sympify 是符号化，与另一个函数 > simplify （化简）拼写相近，不要混淆。

   str_expr = 'x**2 + 2*x + 1'
   expr = sympify(str_expr)
   expr

   

   转换为指定精度的数值解

   可以使用符号变量的 evalf 方法将其转换为指定精度的数值解，例如：

   pi.evalf(3) # pi 保留 3 位有效数字

   

   利用 lambdify 函数将 SymPy 表达式转换为 NumPy 可使用的函数

   如果进行简单的计算，使用 subs 和 evalf 是可行的，但要获得更高的精度，则需要使用更加有效的方法。例如，要保留小数点后 1000 位，则使用 SymPy 的速度会很慢。这时，您就需要使用 NumPy 库。
   lambdify 函数的功能就是可以将 SymPy 表达式转换为 NumPy 可以使用的函数，然后用户可以利用 NumPy 计算获得更高的精度。

   import numpy
   a = numpy.pi / 3
   x = symbols('x')
   expr = sin(x)
   f = lambdify(x, expr, 'numpy')
   f(a)
   0.8660254037844386
   expr.subs(x, pi/3)

   

   使用 simplify (化简)

   在符号计算中，最常用的操作就是利用 simplify 函数对表达式化简。默认情况下，simplify 函数将自行寻找它认为的最简单的表达形式，呈现给用户。

   simplify(sin(x)**2 + cos(x)**2)

   

   alpha_mu = symbols('alpha_mu')
   simplify(2*sin(alpha_mu)*cos(alpha_mu))

   
   由于 simplify 函数执行过程是启发式的，它需要寻找它认为的最简形式，所以有时它的响应会比较慢。所以，当您知道化简形式是什么类型时，不要使用 simplify 函数，而应该使用专门的函数，如 factor（后续将会介绍）。

   多项式和有理函数化简

   下面介绍几个用于多项式或有理函数化简的函数。

   expand (展开)

   将多项式展开，使用 expand 函数。例如：

   x_1 = symbols('x_1')
   expand((x_1 + 1)**2)

   

   factor (因式分解)

   用 factor 函数可以对多项式进行因式分解，例如：

   factor(x**3 - x**2 + x - 1)

   实际上，多项式的展开和因式分解是互逆过程，因此 > factor 和 > expand 也是相对的。

   collect (合并同类项)

   利用 collect 合并同类项，例如：

   expr = x*y + x - 3 + 2*x**2 - z*x**2 + x**3
   collect(expr, x)

   

   cancel (有理分式化简)

   消去分子分母的公因式使用 cancel 函数，例如：

   cancel((x**2 + 2*x + 1)/(x**2 + x))

   

   apart (部分分式展开)

   使用 apart 函数可以将分式展开，例如：

   expr = (4*x**3 + 21*x**2 + 10*x + 12)/(x**4 + 5*x**3 + 5*x**2 + 4*x)
   expr

   

   apart(expr)

   

   微积分符号计算

   在本节中，将介绍使用 SymPy 进行微积分的基本操作。

   一元函数求导函数

   求导函数使用 diff 函数，例如：

   # 求一阶导数
   diff(cos(x), x)

   

   # 求 3 阶导数
   diff(x**4, x, 3)

   
   我们也可以用 符号变量的 diff 方法 求微分，例如：

   expr = cos(x)
   expr.diff(x, 2)

   

   多元函数求偏导函数

   可以用 diff 函数求多元函数的偏导数，例如：
   

   expr = exp(x*y*z)
   diff(expr, x)

   

   integrate (积分)

   使用 integrate 函数求积分，例如：

   # 求不定积分
   integrate(cos(x), x)

   
   求 的定积分：
   注意：在 SymPy 中，我们用 ‘oo’ 表示 > 。

   integrate(exp(-x), (x, 0, oo))

   
   求函数 在 的二重积分：
   

   integrate(exp(-x**2 - y**2), (x, -oo, oo), (y, -oo, oo))

   

   limit (求极限)

   使用 limit 函数求极限，例如：

   limit(sin(x)/x, x, 0)

   
   当 时，求 的极限：

   limit(1/x, x, 0, '+')

   

   series (级数展开)

   使用符号变量的 series 方法可以对函数 在 处进行 阶展开。例如，对函数 在 处进行 阶展开：

   expr = sin(x)
   expr.series(x, 0, 4)

   

   解方程

   使用 solveset 求解方程。

   求解一元二次方程

   求解方程 ，首先要构造方程，使用 Eq 函数构造等式：

   Eq(x**2 - x, 0)

   注意：在 SymPy 中，我们用 > Eq(左边表达式, 右边表达式) 表示左边表达式与右边表达式相等。

   solveset(Eq(x**2 - x, 0), x, domain = S.Reals)

   

比如我们来求解人教版九年级一元二次方程组比较经典的一个题目，

from sympy import *
x,y = symbols('x y')
a,b,c=symbols('a b c')
expr=a*x**2 + b*x + c
s_expr=solve( expr, x)
print(s_expr)

执行之后得出的结果为[(-b + sqrt(-4*a*c + b**2))/(2*a), -(b + sqrt(-4*a*c + b**2))/(2*a)],我们知道根与系数的关系二次方程会有两个解，这里的格式就是一个列表。转为我们常见的数学公式即为：

解二元一次方程组

我们来看如何求解二元一次方程组。（题目来自人教版七年级数学下）

from sympy import *
x,y = symbols('x y')
print(solve([x + y-10,2*x+y-16],[x,y]))

很快就可以得出{x: 6, y: 4}，也就是
。

解三元一次方程组

我们来看如何解三元一次方程组。（题目来自人教版七年级数学下）

执行之后，很快可以得出结果{x: 8, y: 2, z: 2}，也就是

**

求解微分方程

使用 dsolve 函数求解微分方程。首先需要建立符号函数变量：

f = symbols('f', cls = Function)

然后求解微分方程：

diffeq = Eq(f(x).diff(x, 2) - 2*f(x).diff(x) + f(x), sin(x))
diffeq

dsolve(diffeq, f(x))

矩阵运算

我们在进行矩阵运算之前，需要用 Matrix 构造矩阵，例如：

# 构造矩阵
Matrix([[1, -1], [3, 4], [0, 2]])

# 构造列向量
Matrix([1, 2, 3])

# 构造行向量
Matrix([[1], [2], [3]]).T

矩阵转置用矩阵变量的 > T 方法。

# 构造单位矩阵
eye(4)

# 构造零矩阵
zeros(4)

# 构造壹矩阵
ones(4)

# 构造对角矩阵
diag(1, 2, 3, 4)

矩阵转置

矩阵转置用矩阵变量的 T 方法。例如：

a = Matrix([[1, -1], [3, 4], [0, 2]])
a

# 求矩阵 a 的转置
a.T

求矩阵的幂

求矩阵 的 次幂：

# 求矩阵 M 的 2 次幂
M = Matrix([[1, 3], [-2, 3]])
M**2

特殊地，矩阵的 次幂就是矩阵的逆。

# 求矩阵 M 的逆
M**-1

求矩阵的行列式

用矩阵变量的 det 方法可以求其行列式：

M = Matrix([[1, 0, 1], [2, -1, 3], [4, 3, 2]])
M

M.det()

求矩阵的特征值和特征多项式

用矩阵变量的 eigenvals 和 charpoly 方法求其特征值和特征多项式。

M = Matrix([[3, -2,  4, -2], [5,  3, -3, -2], [5, -2,  2, -2], [5, -2, -3,  3]])
M

M.eigenvals()
{3: 1, -2: 1, 5: 2}
lamda = symbols('lamda')
p = M.charpoly(lamda)
factor(p)

Laplace 变换

可以利用 laplace_transform 函数进行 Laplace 变换，例如：

#  Laplace (拉普拉斯)变换
from sympy.abc import t, s
expr = sin(t)
laplace_transform(expr, t, s)

利用 inverse_laplace_transform 函数进行逆 Laplace 变换：

expr = 1/(s - 1)
inverse_laplace_transform(expr, s, t)

利用 SymPy 画函数图像

使用 plot 函数绘制二维函数图像，例如：

from sympy.plotting import plot
from sympy.abc import x
plot(x**2, (x, -2, 2))

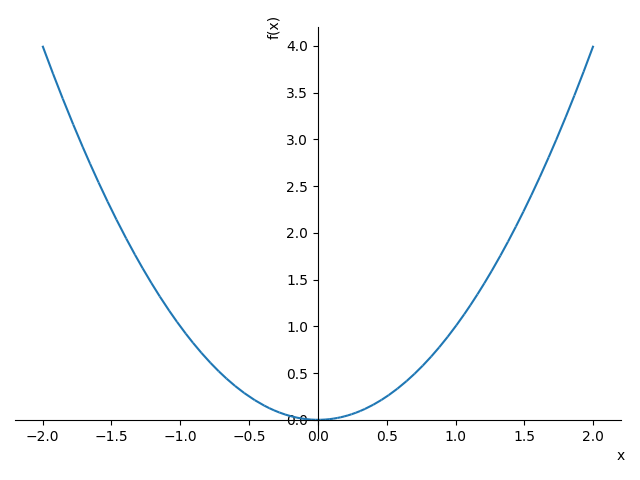
<sympy.plotting.plot.Plot at 0x20d094def40>

导入 SymPy 的 plot_implicit 函数绘制隐函数图像：

from sympy import plot_implicit
from sympy import Eq
from sympy.abc import x, y
plot_implicit(Eq(x**2 + y**2, 1))

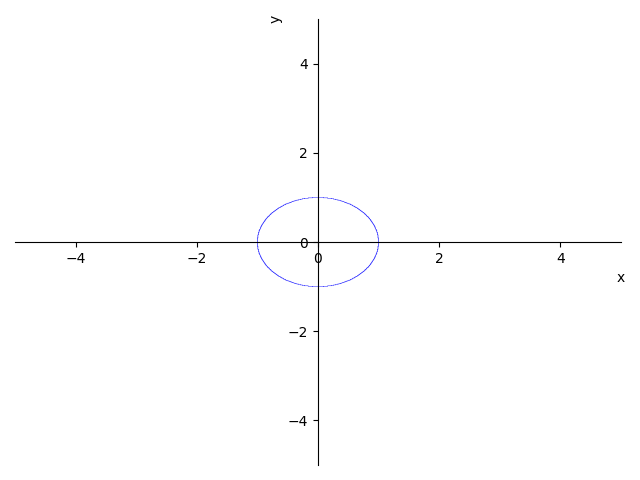
<sympy.plotting.plot.Plot at 0x20d14bb9dc0>

注意：上图中 > 轴不是 > ，导致图像显示不是圆。 使用 SymPy 画出三维函数图像，例如：

from sympy.plotting import plot3d
from sympy.abc import x, y
from sympy import exp
plot3d(x*exp(-x**2 - y**2), (x, -3, 3), (y, -2, 2))

<sympy.plotting.plot.Plot at 0x20d14fd2eb0>

输出运算结果的 代码

使用 latex 函数可以输出运算结果的 代码，例如：

print(latex(integrate(sqrt(x), x)))

结束语

至此，本文就将 SymPy 符号计算库的基本功能和使用技巧介绍完毕，从前面的内容可以总结出如下 2 点结论：

1. SymPy 基于 Python 编写，使用方法继承了 Python 简洁、直白的特点，非常适合初学者快速入门；
2. SymPy 的 2D、3D 函数绘图能力一般，画二维函数时会出现 轴比例不对。用户若有精确绘制函数图像的需求，应该求助于更加专业的 Python 绘图库，如 Matplotlib 。

附录：数学教材推荐

线性代数教材

线性代数特别推荐下面两本教材，这两本书都是华章出品的中文版教材：

• 《线性代数》，史蒂文 J.利昂 (Steven J.Leon)
• 《线性代数及其应用》，戴维 C.雷 (David C.Lay), 史蒂文 R.雷 (Steven R.Lay)

如果你英语比较OK，可以结合的视频教程《麻省理工公开课：线性代数》来看这个视频所用的教材，不过视频录制时间比较早，所用教材也比较落后了，推荐看新版（第4版或第5版）：

• 《Introduction to Linear Algebra》William Gilbert Strang（威廉·吉尔伯特·斯特朗）

同时推荐《线性代数的本质》系列加深理解：
点击查看【bilibili】

微积分教材

微积分教材，简单入门可以看普林斯顿微积分读本以及倚天屠龙，可以主要只看托马斯微积分即可。

• 《普林斯顿微积分读本》（The Calculus Lifesaver:All the Tools You Need to Excel at Calculus）阿德里安·班纳 (Adrian Banner)
• 《托马斯微积分》（Thomas` Calculus）高等教育出版社出版
• 《微积分之屠龙宝刀》和《微积分之倚天宝剑》，C·亚当斯(Colin Adamx) (作者), J·哈斯(Joel Hass) (作者), A·汤普森(Abigail Thompson) (作者)。这两本书书名不忍直视，不要被表面名称误导哦

**

概率统计教材

• 《数理统计与数据分析》(Mathematical Statistics and Data Analysis)JohnA.Rice (作者)
• 《统计学》（Statistics for Engineers and the Sciences）门登霍尔(William Mendenhall), 辛塞奇(Terry Sincich)
• 《统计推断》（Statistical inference） 卡塞拉 (George Casello) (作者), 贝耶 (Roger L.Berger) (作者)

同时推荐看可汗学院的《统计学》：
点击查看【bilibili】

以上教材都要求你使用MATLAB，不过这里建议替换成Python。