什么是插入排序

插入排序(InsertionSort)，一般也被称为直接插入排序。
对于少量元素的排序，它是一个有效的算法。插入排序 是一种最简单的 排序方法 ，它的基本思想是将一个记录插入到 已经排好序 的有序表中，从而一个新的、记录数增 1 的有序表。
在其实现过程使用双层循环，外层循环对除了第一个元素之外的所有元素，内层循环对当前元素前面有序表进行待插入位置查找，并进行移动。

过程图示

假设前面 n-1(其中 n>=2)个数已经是排好顺序的，现将第 n 个数插到前面已经排好的序列中，然后找到合适自己的位置，使得插入第n个数的这个序列也是排好顺序的。
按照此法对所有元素进行插入，直到整个序列排为有序的过程，称为插入排序。
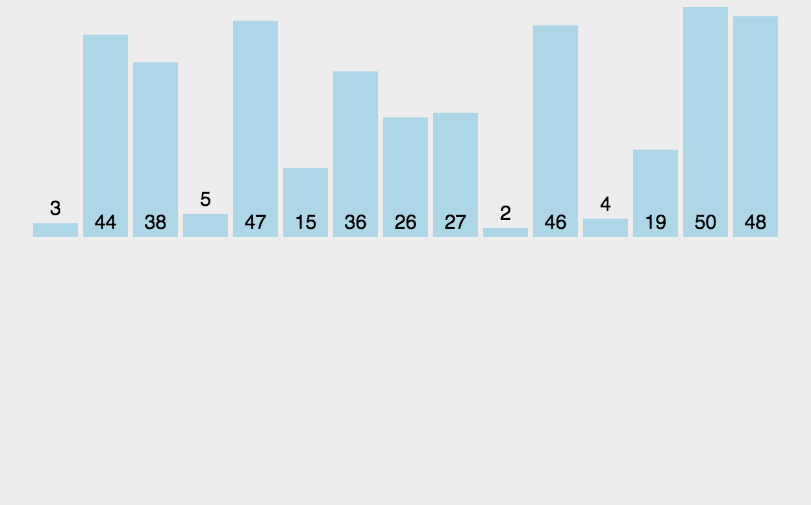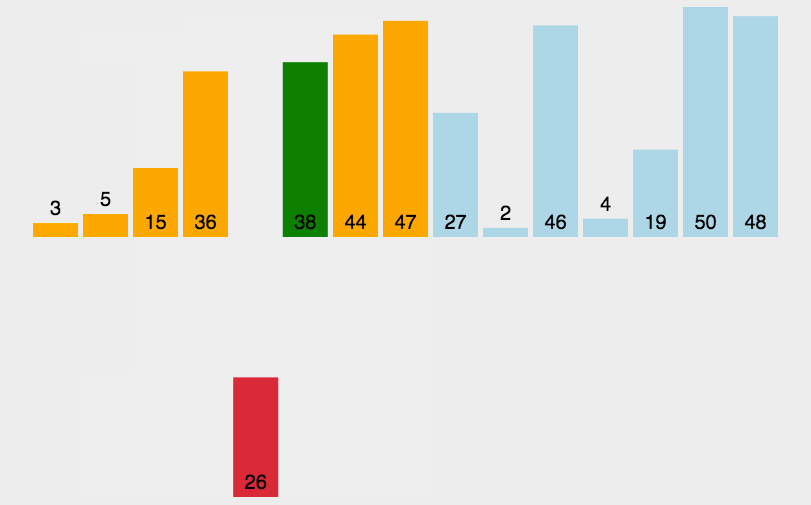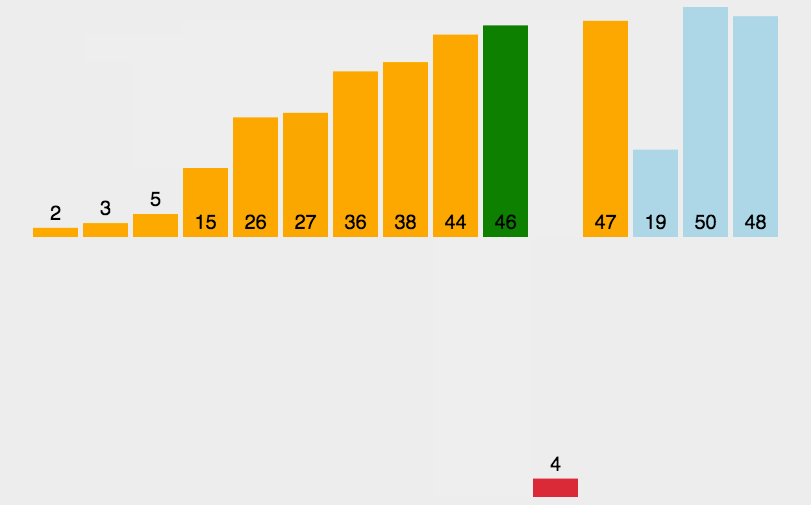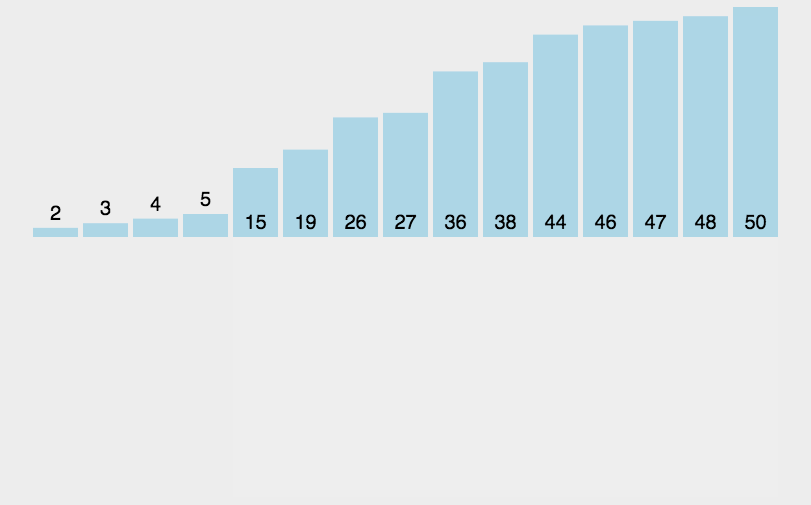
从小到大的插入排序整个过程如图示：
第一轮：从第二位置的 6 开始比较，比前面 7 小，交换位置。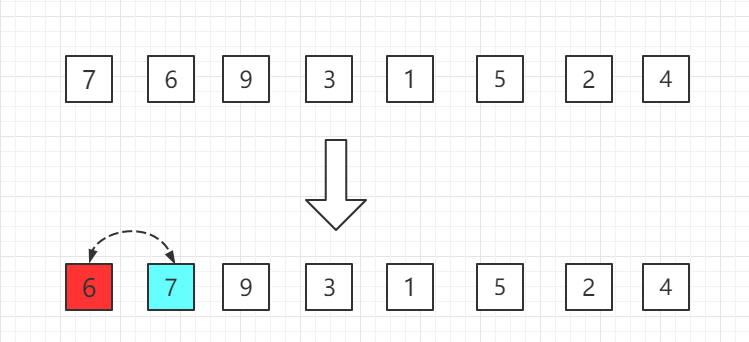

第二轮：第三位置的 9 比前一位置的 7 大，无需交换位置。

第三轮：第四位置的 3 比前一位置的 9 小交换位置，依次往前比较。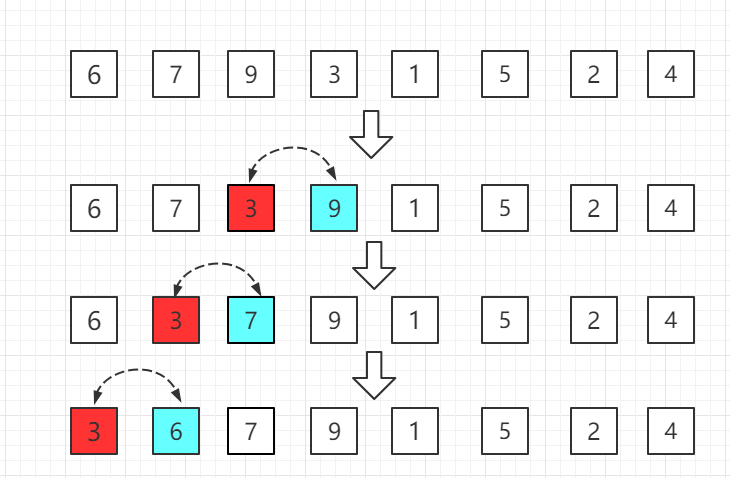

第四轮：第五位置的 1 比前一位置的 9 小，交换位置，再依次往前比较。

……
就这样依次比较到最后一个元素。

动画演示

插入排序和冒泡排序的区别

这里重点说下两种排序方法的区别
假设有这样一个数组为 int []list=new list[]{1,2,3,4}; 我们要对其进行升序排序(很显然 这里已经是符合要求的升序排列).
现在 假若我们用 冒泡排序 大概流程会是这样:

1. 先将1，2进行比较 无须替换 然后2，3比较 无须替换 然后3，4比较 无须替换 完成第一轮冒泡 比较次数为3次
2. 将2，3进行比较 无须替换 然后3，4进行比较 无须替换 完成第二轮冒泡 比较次数为2次
3. 将3，4进行比较 无须替换 完成第三轮冒泡 比较次数为1次

很显然 我们没有移动一次数字 但是却比较了6次。

再来看看插入排序如何实现 其详细步骤为:

1. 先设定1为有序区间 将2和1比较 无须移动 比较一次
2. 此时1，2均为有序区间 将3和2进行比较 无须移动 直接跳出while循环 比较一次
3. 此时1，2，3均为有序区间 将4和3进行比较 无须移动 直接跳出while循环 比较一次

很显然 我们也没有移动数字 但是只比较了3次
总的来说 冒泡排序 循环一次 就确定了第0位为最小值(针对升序) 而插入排序 循环一次 则将有序区间增加一位
因此 针对部分有序的集合来说（这里说的有序 是指与我们想得到的顺序一致） 插入排序效率优于冒泡排序
但是我们可以针对冒泡排序进行优化 当我们循环某一次 发现没有任何数字移动的时候 我们就已经知道 集合已经排序完成 而无须再进行循环。