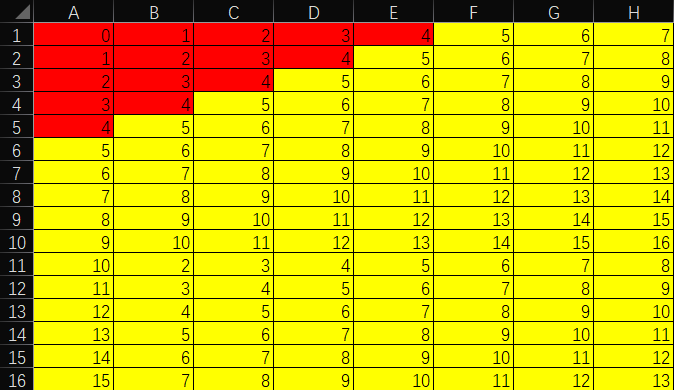
什么是深度优先搜索

深度优先搜索算法（英语：Depth-First-Search,DFS)是一种用于遍历或搜索树或图的算法。其过程简单来说就是对每一个可能的分支深入到不能再深入位置，而且每个节点只能访问一次。

算法题应用场景

1.二叉树有关问题

2.需要从根节点遍历到末尾子节点

3.遍历图

常见题型

满足（最大，最小，某种要求）的深度，路径，节点和……

深度优先搜索的二叉树模板

  1. // 深度优先搜索模板
  2. function dfsSearch() {
  3.   // 初始化当前结果
  4.   let start, currentResult
  5.   // 递归函数
  6.   let dfs = function (node, currentResult) {
  7.     if (!node) { return null }
  8.     // 更新当前结果currentResult
  10.     // 若到达末尾叶子节点，进行最优结果更新
  11.     if (node.left == null && node.right == null) {
  12.       // 更新最优结果
  14.     }
  15.     // 左右子树递归
  16.     dfs(node.left, currentResult)
  17.     dfs(node.right, currentResult)
  18.   }
  19.   dfs(root, start)
  20.   return currentResult
  21. }

判断是否是二叉搜索树

二叉树的中序遍历正好满足二叉搜索树的从小到大的排列规则

  1. const helper = (root, lower, upper) => {
  2.     if (root === null) {
  3.         return true;
  4.     }
  5.     if (root.val <= lower || root.val >= upper) {
  6.         return false;
  7.     }
  8.     return helper(root.left, lower, root.val) && helper(root.right, root.val, upper);
  9. }
  10. var isValidBST = function(root) {
  11.     return helper(root, -Infinity, Infinity);
  12. };

对无向图的深度优先搜索

  1. 获取二维数组的长宽
  2. 遍历并添加边界条件递归调用DFS函数

  3. 初始化调用DFS函数

    机器人行走范围

    image.png

    对无向图的深度优先搜索模板(岛屿数量）

    1. function get(arr) {
    2. // 通常输入的数组都是二维数组
    3. let m = arr.length
    4. let n = arr[0].length
    5. let count = 0
    6. function dfs(i, j) {
    7.  // 跳出递归的边界条件
    8.  if (i < 0 || j < 0 || i >= m || j >= n) return
    9.  // 按照题中所给的要求递归遍历无向图
    10.  dfs(i - 1, j) || dfs(i + 1, j) || dfs(i, j - 1) || dfs(i, j + 1)
    11. }
    13. for (let i = 0; i < m; i++) {
    14.  for (let j = 0; j < n; j++) {
    15.    // 符合题目的条件添加进结果或者计数
    16.    if (arr[i][j] == 1) {
    17.      // 更细最新结果
    18.      count++
    19.      dfs(i, j)
    20.    }
    21.  }
    23. }
    24. return count
    25. }

    图像渲染

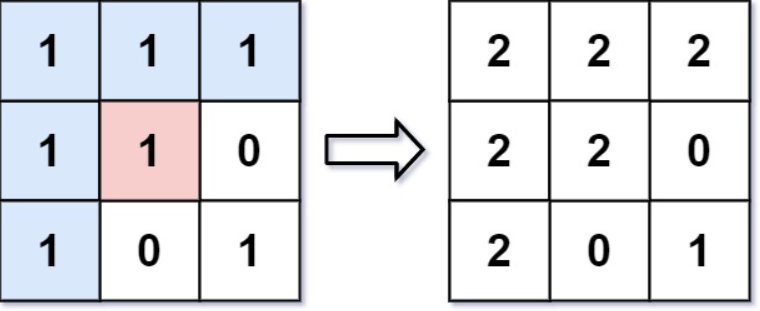
    image.png

    1. var floodFill = function (image, sr, sc, newColor) {
    2. let m = image.length
    3. let n = image[0].length
    4. let oldColor = image[sr][sc]
    5. if (newColor == oldColor) {
    6.  return image
    7. }
    8. let dfs = function (i, j) {
    9.  if (i < 0 || j < 0 || i >= m || j >= n || image[i][j] !== oldColor) {
    10.    return
    11.  }
    12.  image[i][j] = newColor
    13.  dfs(i + 1, j) || dfs(i, j + 1) || dfs(i, j - 1) || dfs(i - 1, j)
    14. }
    15. dfs(sr, sc)
    16. return image
    17. };

    深拷贝的深度优先搜索

不需要创建函数的DFS

路径总和

:::tips 给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。 :::

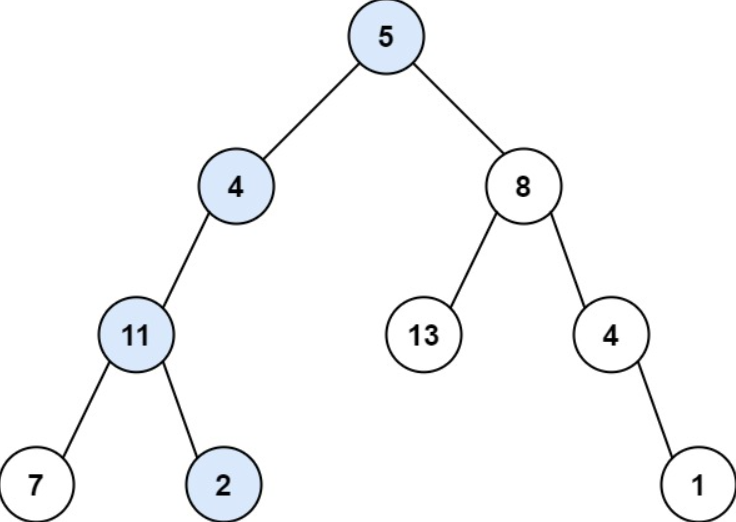
:::tips 输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。 ::: :::tips 输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 —> 2): 和为 3
(1 —> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。 ::: :::tips 输入：root = [], targetSum = 0 输出：false 解释：由于树是空的，所以不存在根节点到叶子节点的路径。 ::: image.png

  1. var hasPathSum = function(root, targetSum) {
  2.   if(root === null) {
  3.         return false
  4.     }
  5.     // 搜到叶子节点，则判断当前节点值是否等于目标值
  6.     if(root.left === null && root.right === null) {
  7.         return root.val === targetSum
  8.     }
  9.     // 还没搜到叶子节点，则进行 目标值-当前节点值，并继续往下搜
  10.     return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val)
  11. };

路径总和ii

输出全部满足的路径数组

  1. /**
  2.  * @param {TreeNode} root
  3.  * @param {number} targetSum
  4.  * @return {number[][]}
  5.  */
  6. var pathSum = function (root, targetSum) {
  7.   let res = [];
  8.   let path = [];
  9.   const dfs = (root, targetSum) => {
  10.     // 如果节点为空则不需要再递归了
  11.     if (root == null) {
  12.       return;
  13.     }
  14.     // 把当前节点的值加入路径中
  15.     path.push(root.val);
  16.     // 由于路径中加入了当前节点，那目标值就少了
  17.     targetSum -= root.val;
  18.     if (root.left == null && root.right == null && targetSum == 0) {
  19.       // 如果到达叶子节点 并且目标值满足
  20.       res.push(path.slice());
  21.       // res.push(path.concat());
  22.     }
  23.     dfs(root.left, targetSum);
  24.     dfs(root.right, targetSum);
  25.     // 左右子节点都递归完了，把当前节点从路径中删除，可走下一条路径
  26.     path.pop();
  27.   };
  28.   dfs(root, targetSum);
  29.   return res;
  30. };

路径总和iii

image.png

  1. var sumNumbers = function (root) {
  2.   return dfs(root, 0)
  3. };
  5. let dfs = function (root, prevSum) {
  6.   if (!root) {
  7.     return 0
  8.   }
  9.   let sum = prevSum * 10 + root.val
  10.   if (!root.left && !root.right) {
  11.     return sum
  12.   }
  13.   return dfs(root.left, sum) + dfs(root.right, sum)
  14. }

判断两个二叉树是否相等

  1. var isSameTree = function(p, q) {
  2.     if(!p && !q) 
  3.         return true;
  4.     if(!p || !q) 
  5.         return false;
  6.     if(p.val != q.val) 
  7.         return false;
  8.     return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
  9. }

单词搜索

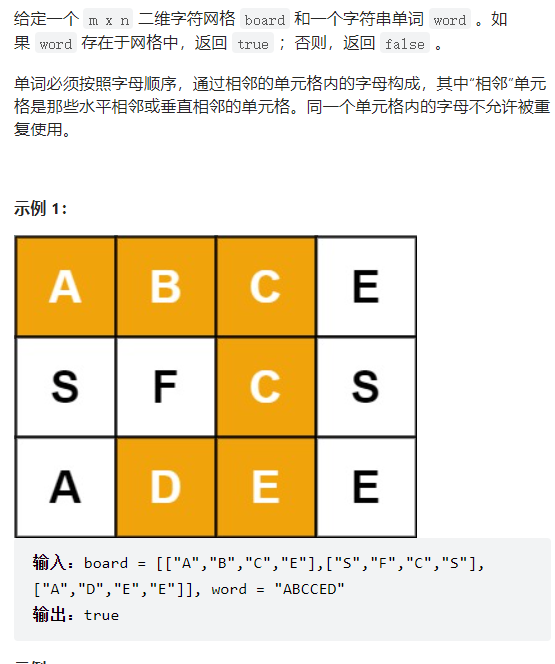
image.png
image.png

  1. var exist = function(board, word) {
  2.   const W = board.length;
  3.   const H = board[0].length
  4.   const K = word.length
  6.   //搜索的方向
  7.   const dirs = [[0, -1], [1, 0],[0, 1],[-1, 0]]
  8.   function helper(i, j, k) {
  9.     if (k>=K) return true
  10.     if (i >= W || j >= H || i < 0 || j < 0) return false
  12.     if (board[i][j] !== word[k]) return false
  13.     board[i][j]='*'
  14.     for (let [x,y] of dirs) {
  15.       if(helper(i+x,j+y,k+1)) return true
  16.     }
  17.     board[i][j]=word[k]
  18.     return false
  19.   }
  20.   for (let i = 0; i < W; i++) {
  21.     for (let j = 0; j < H; j++) {
  22.       if (helper(i,j,0)) return true
  23.     }
  24.   }
  25.   return false
  26. };