什么是广度优先搜索

广度优先搜索算法（英语：Breadth-First-Search，缩写为BFS），又译作宽度优先搜索，或横向优先搜索，是一种图形搜索算法。简单的说，BFS是从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。广度优先搜索的实现一般采用open-closed表。

时间复杂度：最差情形下，BFS必须查找所有到可能节点的所有路径。

完全性：广度优先搜索算法具有完全性。这意指无论图形的种类如何，只要目标存在，则BFS一定会找到。然而，若目标不存在，且图为无限大，则BFS将不收敛（不会结束）。

最佳解：若所有边的长度相等，广度优先搜索算法是最佳解——亦即它找到的第一个解，距离根节点的边数目一定最少；但对一般的图来说，BFS并不一定回传最佳解。这是因为当图形为加权图（亦即各边长度不同）时，BFS仍然回传从根节点开始，经过边数目最少的解；而这个解距离根节点的距离不一定最短。这个问题可以使用考虑各边权值，BFS的改良算法成本一致搜索法来解决。然而，若非加权图形，则所有边的长度相等，BFS就能找到最近的最佳解。
最后，广度优先搜索是可以于计算机游戏中平面网络的。

广度优先搜索的应用场景

BFS可用来解决计算机游戏（例如即时策略游戏）中找寻路径的问题。在这个应用中，使用平面网格来代替图形，而一个格子即是图中的一个节点。所有节点都与它的邻居（上、下、左、右、左上、右上、左下、右下）相接。
值得一提的是，当这样使用BFS算法时，首先要先检验上、下、左、右的邻居节点，再检验左上、右上、左下、右下的邻居节点。这是因为BFS趋向于先查找斜向邻居节点，而不是四方的邻居节点，因此找到的路径将不正确。BFS应该先查找四方邻居节点，接着才查找斜向邻居节点1。
最短路径问题一般用bfs，或者需要一层层判断或者遍历二叉树的时候需要用bfs。

广度优先实例

二叉树的层序遍历

  1. var levelOrder = function (root) {
  2.   // 若root不为空
  3.   if (root) {
  4.     // 创建一个队列和目标数组存储节点的值
  5.     // 创建一个队列,并放入根节点的值
  6.     let queen = [root]
  7.     // 初始化该目标数组为空数组
  8.     let res = []
  9.     // 若该队列内存在元素
  10.     while (queen.length > 0) {
  11.       // 将该队列内首个元素推出队列
  12.       let current = queen.shift()
  13.       // 若该队列推出的值不为空
  14.       if (current !== null) {
  15.         // 将该节点值推入目标数组
  16.         res.push(current.val)
  17.         // 将该节点的左右孩子推入队列
  18.         queen.push(current.left)
  19.         queen.push(current.right)
  20.       }
  21.       if (current == null) {
  22.         continue
  23.       }
  24.     }
  25.     return res
  26.   }
  27. };
  30. // 二叉树层序遍历输出每层的节点
  31. // 例如：输入：
  32. // root = [3,9,20,null,null,15,7]
  33. // 输出：[[3],[9,20],[15,7]]
  34. var levelOrder = function(root) {
  35.   const ret = [];
  36.     if (!root) {
  37.         return ret;
  38.     }
  40.     const q = [];
  41.     q.push(root);
  42.     while (q.length !== 0) {
  43.         const currentLevelSize = q.length;
  44.         ret.push([]);
  45.         for (let i = 1; i <= currentLevelSize; ++i) {
  46.             const node = q.shift();
  47.             ret[ret.length - 1].push(node.val);
  48.             if (node.left) q.push(node.left);
  49.             if (node.right) q.push(node.right);
  50.         }
  51.     }
  52.     return ret;
  53. };
  56. // 填充每个节点的下一个右侧指针
  57. var connect = function(root) {
  58.     if (root === null) {
  59.         return root;
  60.     }
  61.     // 初始化队列同时将第一层节点加入队列中，即根节点
  62.     const Q = [root]; 
  63.     // 外层的 while 循环迭代的是层数
  64.     while (Q.length > 0) {
  65.         // 记录当前队列大小
  66.         const size = Q.length;
  67.         // 遍历这一层的所有节点
  68.         for(let i = 0; i < size; i++) {
  69.             // 从队首取出元素
  70.             const node = Q.shift();
  71.             // 连接
  72.             if (i < size - 1) {
  73.                 node.next = Q[0];
  74.             }
  75.             // 拓展下一层节点
  76.             if (node.left !== null) {
  77.                 Q.push(node.left);
  78.             }
  79.             if (node.right !== null) {
  80.                 Q.push(node.right);
  81.             }
  82.         }
  83.     }
  84.     // 返回根节点
  85.     return root;
  86. };

后继者

  1. var inorderSuccessor = function (root, p) {
  2.   // 输出指定的p节点的中序遍历的下一个节点
  3.   let stack = [], prev = null, cur = root
  4.   while (cur || stack.length) {
  5.     while (cur) {
  6.       stack.push(cur)
  7.       cur = cur.left
  8.     }
  9.     cur = stack.pop()
  10.     if (prev === p) {
  11.       return cur
  12.     }
  13.     prev = cur
  14.     cur = cur.right
  15.   }
  17. };

二叉树的锯齿状层序遍历

  1. var zigzagLevelOrder = function(root) {
  2. if (!root) {
  3.         return [];
  4.     }
  6.     const ans = [];
  7.     const nodeQueue = [root];
  9.     let isOrderLeft = true;
  11.     while (nodeQueue.length) {
  12.         let levelList = [];
  13.         const size = nodeQueue.length;
  14.         for (let i = 0; i < size; ++i) {
  15.             const node = nodeQueue.shift();
  16.             if (isOrderLeft) {
  17.                 levelList.push(node.val);
  18.             } else {
  19.                 levelList.unshift(node.val);
  20.             }
  21.             if (node.left !== null) {
  22.                 nodeQueue.push(node.left);
  23.             }
  24.             if (node.right !== null) {
  25.                 nodeQueue.push(node.right);
  26.             }
  27.         }            
  28.         ans.push(levelList);
  29.         isOrderLeft = !isOrderLeft;
  30.     }
  32.     return ans;
  33. };

BFS使用队列，把每个还没有搜索到的点依次放入队列，然后再弹出队列的头部元素当做当前遍历点。

BFS总共有两个模板：

模板一：
如果不需要确定当前遍历到了哪一层，BFS 模板如下。

  1. while queue 不空：
  2.     cur = queue.pop() // shift
  3.     if cur 有效且未被访问过：
  4.         进行处理
  5.     for 节点 in cur 的所有相邻节点：
  6.         if 该节点有效：
  7.             queue.push(该节点)

模板二：
如果要确定当前遍历到了哪一层，BFS 模板如下。
这里增加了 level 表示当前遍历到二叉树中的哪一层了，也可以理解为在一个图中，现在已经走了多少步了。size 表示在当前遍历层有多少个元素，也就是队列中的元素数，我们把这些元素一次性遍历完，即把当前层的所有元素都向外走了一步。

  1. level = 0
  2. while queue 不空：
  3. size = queue.size()
  4. while (size --) {
  5.   cur = queue.pop() // shift
  6.   if cur 有效且未被访问过：
  7.   进行处理
  8.   for 节点 in cur的所有相邻节点：
  9.   if 该节点有效：
  10.   queue.push(该节点)
  11. }
  12.     level ++;
  13. }

恢复搜索二叉树

题目：恰好有两个值位置更换了，请还原搜索二叉树。

中序遍历BST，依次访问的节点值是递增的，错误的BST会破坏递增性，从而能定位出错误。
错误有两种：

错误1：出现了两对不满足前小后大，需要交换第一对的第一个元素与第二对的第二个元素。
错误2：只出现一对不满足前小后大，交换这一对元素即可。

可以在的递归遍历过程中，将节点值推入一个数组，再遍历数组找出错误对。
但其实没必要。
只用比较前后访问的节点值，prev 保存上一个访问的节点，当前访问的是 root 节点。

每访问一个节点，如果prev.val>=root.val，就找到了一对“错误对”。
检查一下它是第一对错误对，还是第二对错误对。

遍历结束，就确定了待交换的两个错误点，进行交换。

const recoverTree = (root) => {
    let perv = new TreeNode(-Infinity);
    let err1, err2 = null;

    const inOrder = (root) => {
        if (root == null) {
            return;
        }
        inOrder(root.left);

        if (perv.val >= root.val && err1 == null) { // 当前是第一对错误
            err1 = perv;                            // 记录第一个错误点
        }
        if (perv.val >= root.val && err1 != null) { // 第一个错误点已确定
            err2 = root;                            // 记录第二个错误点
        }
        perv = root;       // 更新 perv

        inOrder(root.right);
    };

    inOrder(root);
    const temp = err1.val;
    err1.val = err2.val;
    err2.val = temp;
};

判断是否为轴对称二叉树

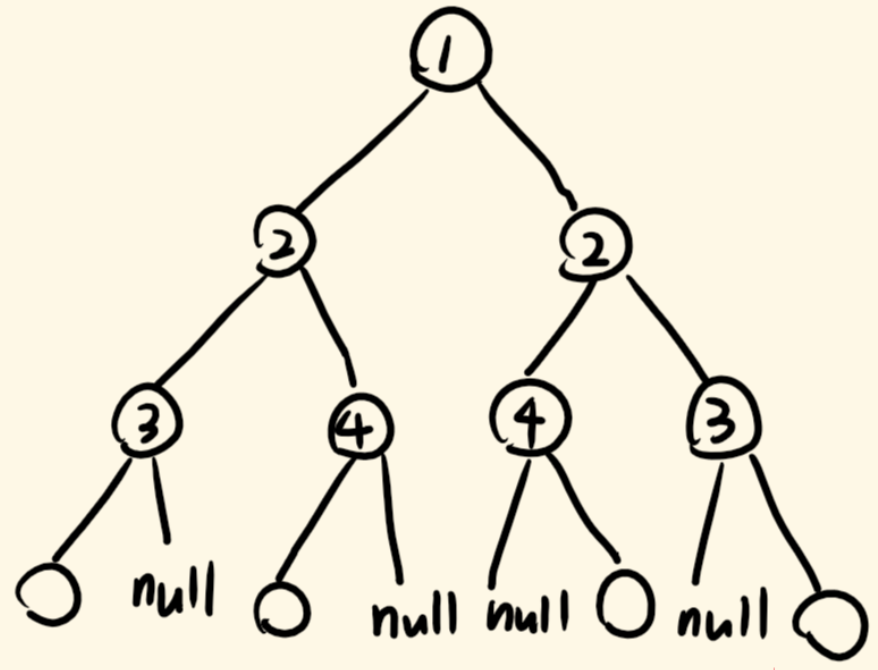
image.png

const isSymmetric = (root) => {
  if (root == null) return true; 

  const queue = [];
  queue.push(root.left, root.right);  // 起初入列两个子树

  while (queue.length) {  // 队列清空就结束，没有节点可入列了
    const levelSize = queue.length; // 当前层的节点个数
    for (let i = 0; i < levelSize; i += 2) { // 当前层的节点成对出列
      const left = queue.shift();   
      const right = queue.shift();  // 出列一对节点
      if ((left && right == null) || (left == null && right)) { // 一个存在 一个不存在
        return false;
      }
      if (left && right) { // 两个都存在
        if (left.val != right.val) { // 节点值不同，不对称
          return false;
        }
        queue.push(left.left, right.right); // 推入下一层的一对节点
        queue.push(left.right, right.left); // 推入下一层的一对节点
      }
    }
  }
  return true; // bfs结束，始终没有返回false，则返回真
};
  • 维护一个队列，起初，根节点（如果存在）的左右子树入列
  • 每次出列一对节点，考察它们俩是否对称
    • 如果不对称，那整个树就不对称，结束BFS，如果对称，则下一对节点入列
    • 哪些情况不对称：
      • 一个为 null 一个不为 null，直接返回 false
      • 都存在，但 root 值不同，直接返回 false
    • 将这俩节点的子树成对入列，继续考察，入列的顺序是：
  1. 左子树的左子树，右子树的右子树，入列，它们这对被考察
  2. 左子树的右子树，右子树的左子树，入列，它们这对被考察

课程表

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。 请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例1

输入：numCourses = 2, prerequisites = [[1,0]] 输出：true 解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

示例2

输入：numCourses = 2, prerequisites = [[1,0],[0,1]] 输出：false 解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

const canFinish = (numCourses, prerequisites) => {
  let inDegree = new Array(numCourses).fill(0)
  let map = {}
  for(let i = 0 ;i<prerequisites.length;i++){
      inDegree[prerequisites[i][0]]++
      if(map[prerequisites[i][1]]){
          map[prerequisites[i][1]].push(prerequisites[i][0])
      }else{
          map[prerequisites[i][1]] = [prerequisites[i][0]]
      }
  }
  let queue = []
  for(let i = 0;i<inDegree.length;i++){
      if(inDegree[i] == 0){
      queue.push(i)
      }
  }
  let count = 0
  while(queue.length){
      let selected = queue.shift()
      count++
      let toDegree = map[selected]
      if(toDegree && toDegree.length){
          for (let i = 0; i < toDegree.length; i++) {
        inDegree[toDegree[i]]--;             // 依赖它的后续课的入度-1
        if (inDegree[toDegree[i]] == 0) {    // 如果因此减为0，入列
          queue.push(toDegree[i]);
        }
      }
      }
  }
  return count == numCourses
};

什么时候用bfs，什么时候用dfs

bfs一般是用来入队列，出队列的操作，dfs一般用入栈出栈的操作。
DFS的特点是不具有BFS中按层次顺序遍历的特性，所以DFS不具有最优性。DFS因此常用来求解有没有的问题。DFS所得到的解不一定是最优解。当题目中出现问题是否有解等字眼时，常用DFS来求解。

BFS的特点是按照层次顺序遍历，因此，BFS可以用来求解最优解，当题目中出现最短路径，最少的时间等字眼时，常用BFS来求解。