前言
从数组中查找你需要的数据,是一个很常见的需求,那么当你查找所需数据时,用什么方法查找速度最快?
本文将通过图文形式,详细讲解线性查找与二分查找,并用JavaScript将其实现,欢迎各位感兴趣的前端开发者阅读本文。
线性查找
概念
线性查找是一种在数组中查找数据的算法,从数组的头部开始按顺序往下查找即为线性查找。
图解示例
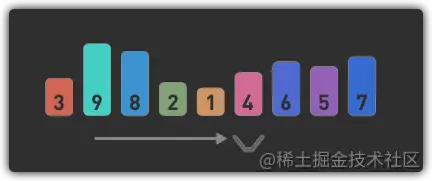
如图所示,我们查找数字6在数组中的位置
- 从数组的最左边开始查找,将其与6进行比较,如果结果一致,查找便结束,不一致则向右检查下一个数字。

- 此处不一致,所以向右继续和下一个数字进行比较。

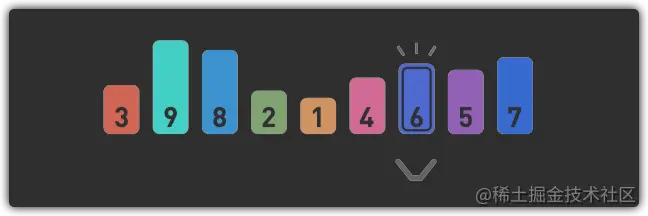
- 重复上述操作直到找到数字6为止
- 找到6了,查找结束
线性查找需要从头开始不断地按顺序检查数据,因此在数据量大且目标数据靠后,或者目标数据不存在时,比较的次数就会更多,也更为好使。若数据量为n,线性查找的时间复杂便为O(n)。
用JS实现线性查找
正如图解示例所述,我们想要查找某个值在数组中的位置,需要遍历这个数组,判断当前遍历到的值是否与目标值相等。
- 声明一个函数,参数为:需要查找的数组,需要查找的数据
- 遍历数组
- 比较需要查找的数据是否与当前遍历到的数据相等
- 如果相等则返回当前元素的位置,结束循环
接下来,我们将上述实现思路转化为代码
- 编写线性查找函数 ```javascript /* 线性查找函数
- @param arr 需要进行查找的数组
- @param target 需要查找的数据
- @returns {number} 返回值
*/ const linearSearch = function (arr,target) {
// 目标元素位置
let position = -1; for (let i = 0; i < arr.length; i++){ // 如果当前遍历到的值与目标值相等则返回目标元素的位置
if(arr[i] === target){
}position = i;return position;
}
return position; }接下来,我们测试下刚才编写的线性查找函数 ```javascript const dataArr = [3,9,8,2,1,4,6,5,7]; const position = linearSearch(dataArr,6); if(position !== -1){ console.log(`目标元素在数组中的位置:${position}`); }else{ console.log("目标元素不在数组中"); }
二分查找
概念
二分查找也是一种在数组中查找数据的算法,它只能查找已经排序好的数据。
二分查找通过比较数组中间的数据与目标数据的大小,可以得知目标数据是在数组的左边还是右边。
因此,比较一次就可以把查找范围缩小一半。重复执行该操作接可以找到目标数据,或者得出目标数据不存在的结论。图解示例
如图所示,我们查找数字6在数组中的位置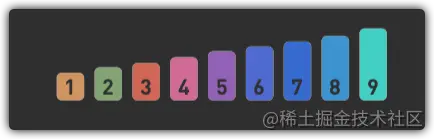
- 首先,找到数组中间的数字,此处为5.
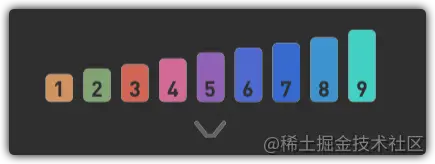
- 将5和要查找的数字6进行比较
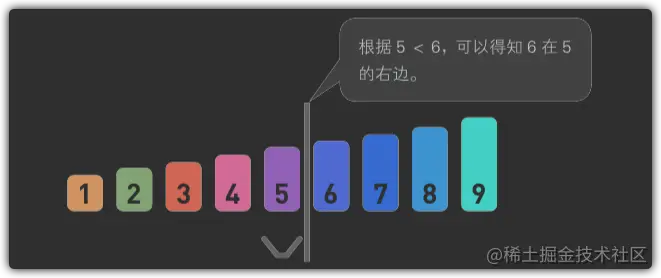
- 把不需要的数字移出查找范围

- 在剩下的数组中找到中间的数字,此处为7

- 比较6和7

- 把不需要的数字移出查找范围
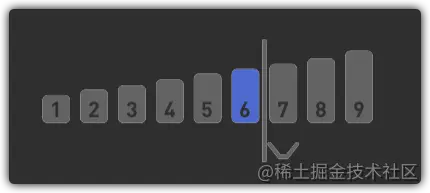
- 在剩下的数组中找到中间的数字,此处为6

- 6=6,成功找到目标数字
用JS实现二分查找
正如图解示例所述,二分查找只能查找已经排序好的数据,每一次查找都可以将查找范围减半,查找范围内只剩一个数据时查找结束。
- 声明一个函数,参数为:要查找的数组,要查找的数据,数组的起点,数组的末尾
- 找到数组的中间值,将其与目标值进行比较
- 如果中间值大于目标值,可知目标值在中间值的左侧,则对其左边的数据执行上述操作
- 如果中间值小于目标值,可知目标值在中间值的右侧,则对其右边的数据执行上述操作
- 直至中间值等于目标值,则结束上述操作,返回中间值的位置。
我们将上述思路转化为代码
- 编写二分查找函数
```javascript
/* 二分查找 @param arr 查找的数组
@param target 查找的数据
*@param start 数组的开始位置
- @param end 数组的末尾位置
- @returns {number} */
const binarySearch = function (arr,target,start,end) {
let targetPosition = -1;
// 计算中间值
const median = Math.floor((start + end) / 2);
// 判断中间值与目标值是否相等
if(arr[median] === target){
targetPosition = median;
return targetPosition;
}
// 未找到
if(start >= end){
return targetPosition;
}
// 判断中间值是否大于目标值
if(arr[median] > target){
// 递归中间值左侧的数组
return binarySearch(arr,target,start,median - 1)
}else{
// 递归中间值右侧的数组
return binarySearch(arr,target, median + 1, end);
} };
// 接下来,我们来测试下刚才编写的二分查找函数
const dataArr = [1,2,3,4,5,6,7,8,9];
const position = binarySearch(dataArr,6,0,dataArr.length - 1);
if(position !== -1){
console.log(目标元素在数组中的位置:${position})
}else{
console.log(“目标元素不在数组中”);
}

<a name="Drp9s"></a>
## 线性查找与二分查找的区别
<a name="aw2a7"></a>
### 本质区别
线性查找可以从乱序数组中找数据,而二分查找只能从已排序好的数组中查找数据。
<a name="WsMlv"></a>
### 性能
二分查找利用已排序好的数组,每一次查找都可以将查找范围减半。如果将数量为n的数组,将其长度减半log2n次后,其中便只剩一个数据了,因此它的时间复杂度为O(logn)<br />线性查找需要从头开始不断地按顺序检查数据,因此在数量大且目标数据靠后,或者目标数据不存在时,比较的次数就会更多,也更为耗时。如果数组的数据量为n,线性查找的时间复杂度便为O(n)<br />从时间复杂度上分析,二分查找相比线性查找速度得到了指数倍的提升。
<a name="IrGdp"></a>
### 使用场景
线性查找,数组中的数据可以是无序的,添加数据时无需顾虑位置,直接将其插入到数组的末尾即可,不需要耗费时间。<br />二分查找,数组中的数据必须是有序的,添加数据时就需要考虑位置,需要消耗一定的时间。<br />综合上述,如果你查找数据比较频繁的话二分查找更适合你,否则线性查找更适合你。
作者:神奇的程序员<br />链接:https://juejin.cn/post/6844904130570354696<br />来源:稀土掘金<br />著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
<a name="xHtBx"></a>
# 二分查找的应用示例
<a name="A803i"></a>
## 1.查找数组中元素的索引
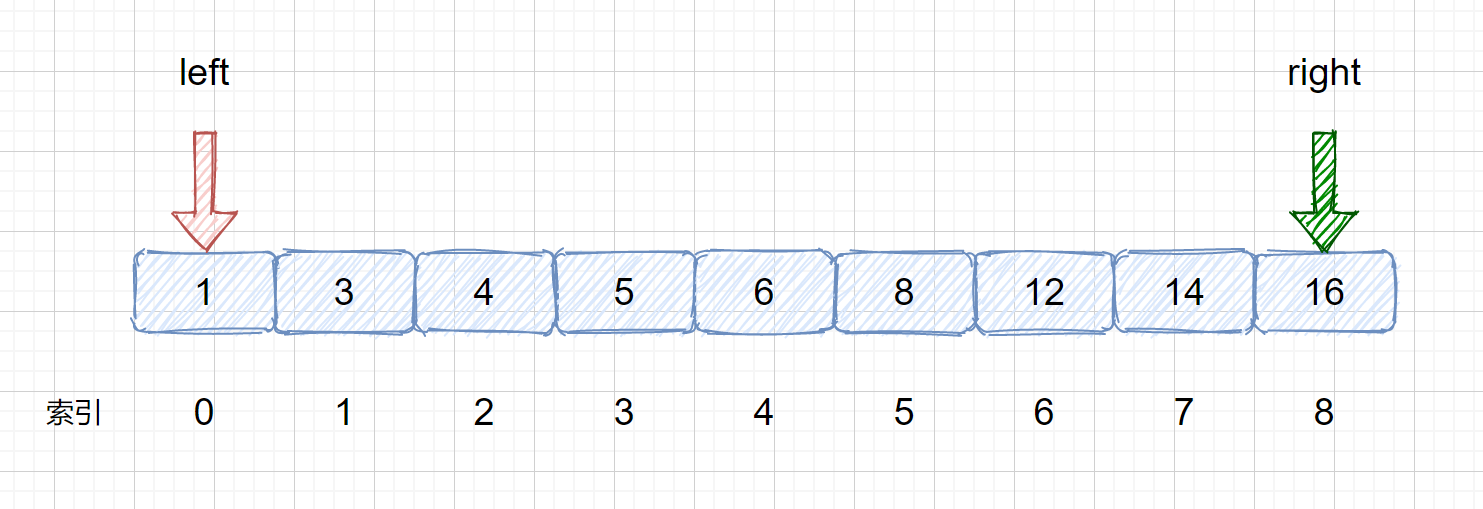
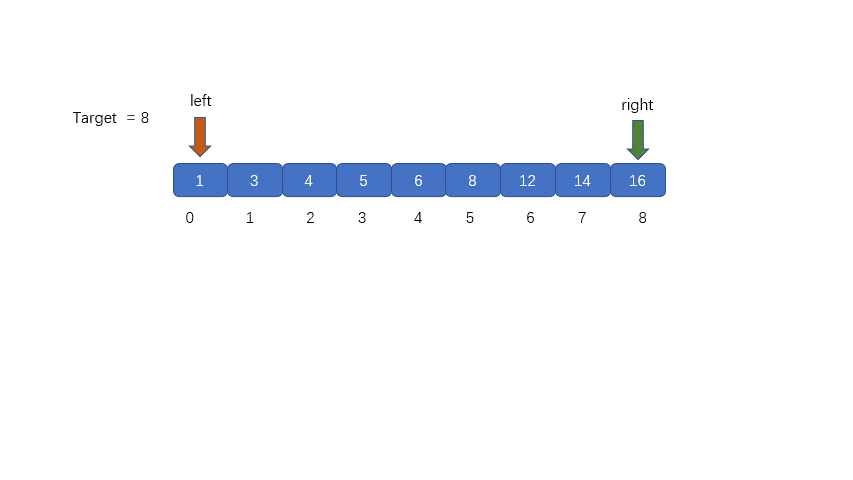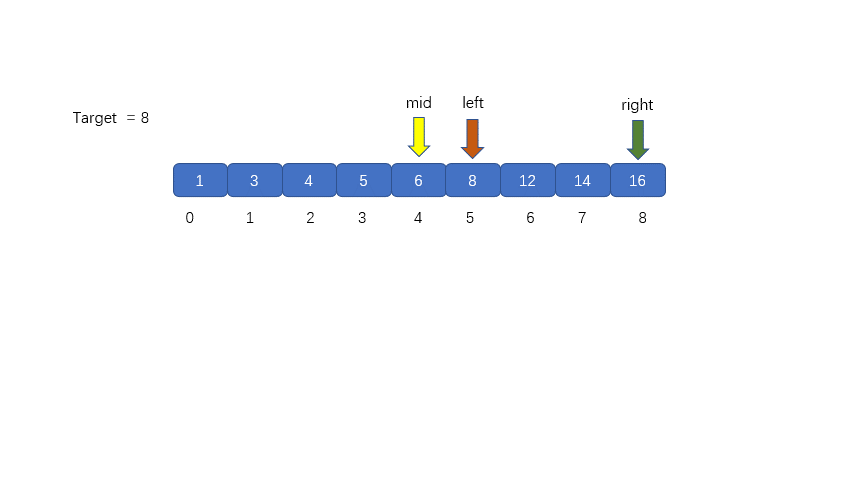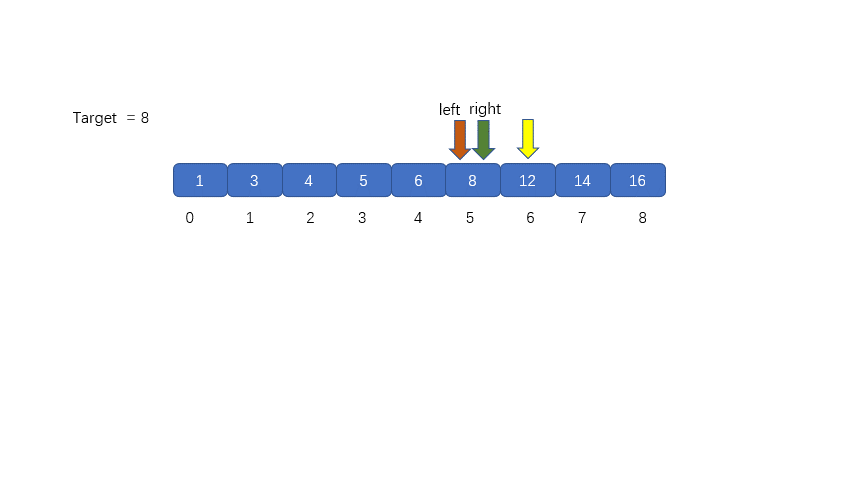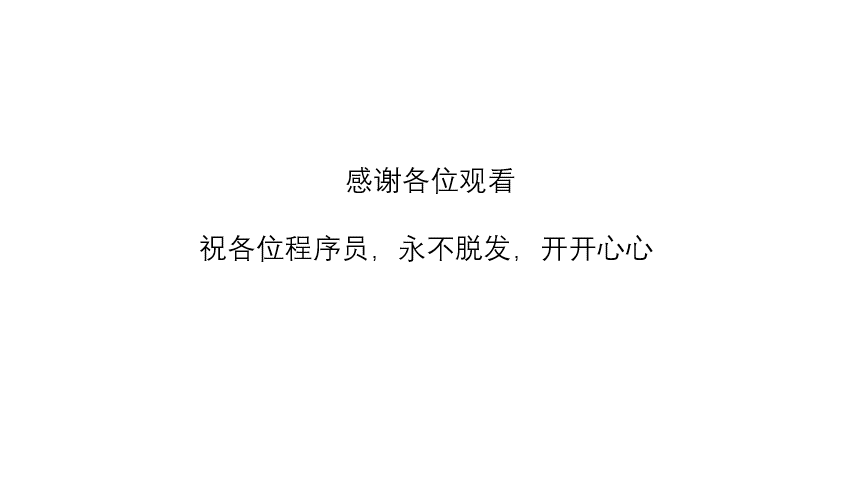
`nums = {1,3,4,5,6,8,12,14,16}; target = 8`<br />**解析:**
> 我们需要定义两个指针分别指向数组的头部及尾部,这是我们在整个数组中查询的情况,当我们在数组
> 某一区间进行查询时,可以输入数组,起始位置,终止位置进行查询。
> 
> 找出mid,该索引为 `mid =(left + right)/ 2`,但是这样写有可能溢出,所以我们需要改进一下写成
> `mid = left +(right - left)/ 2` 或者 `left + ((right - left ) >> 1) `两者作用是一样的,都是为了找到两指针的中间索引,使用位运算的速度更快。那么此时的 `mid = 0 + (8-0) / 2 = 4`
> 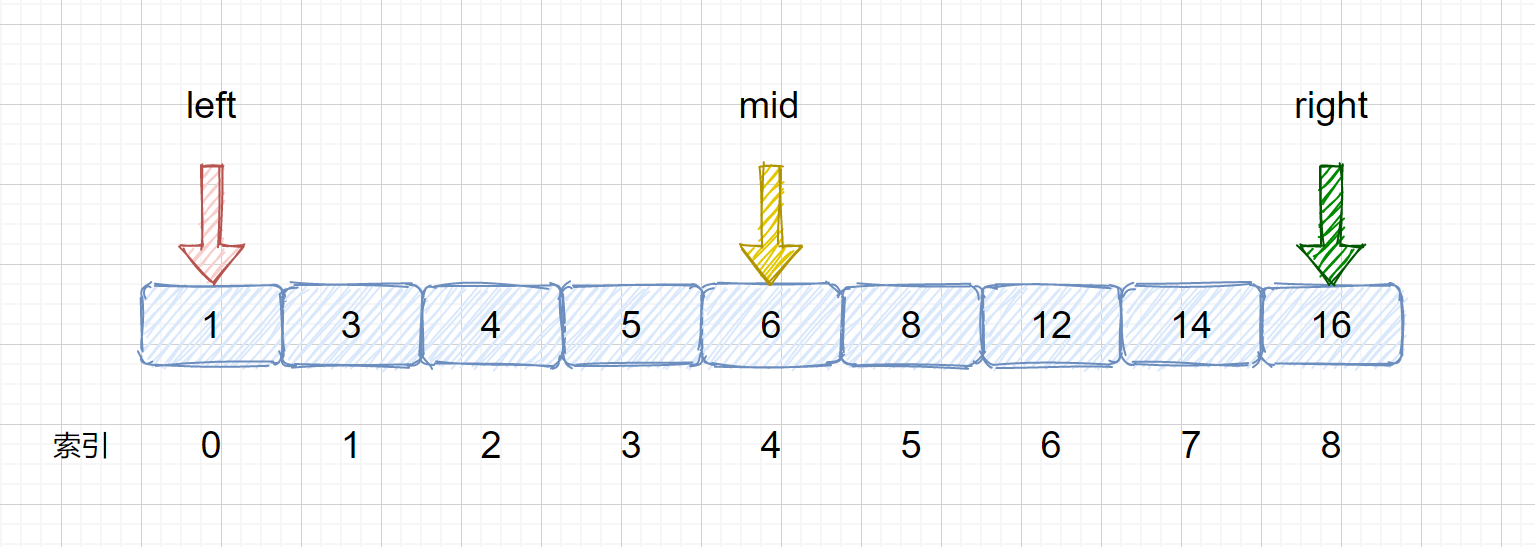
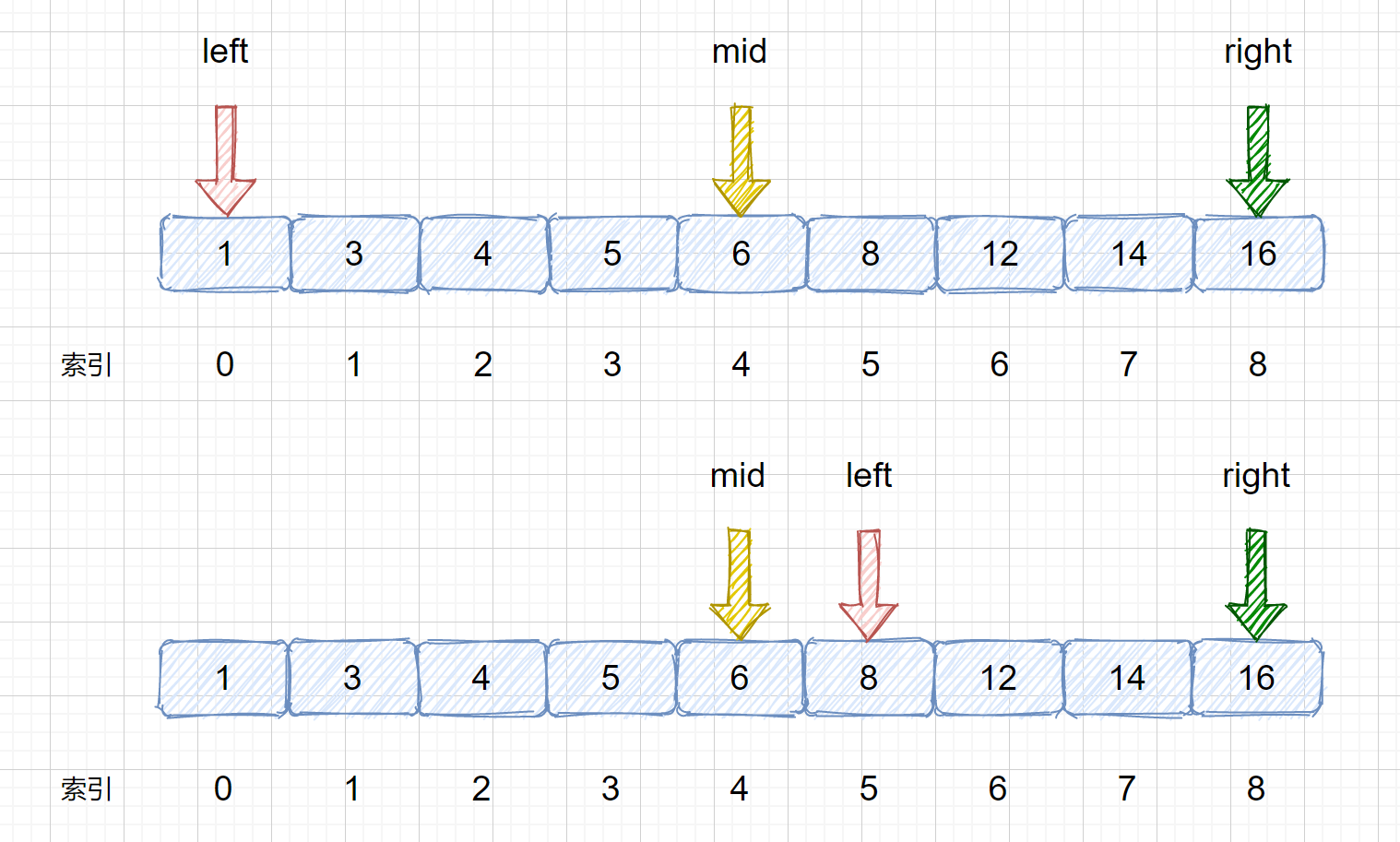
> 此时我们的 `mid = 4`,`nums[mid] = 6 < target`,那么我们需要移动我们的 left 指针,
> 让`left = mid + 1`,下次则可以在新的 left 和 right 区间内搜索目标值,下图为移动前和移动后
> 
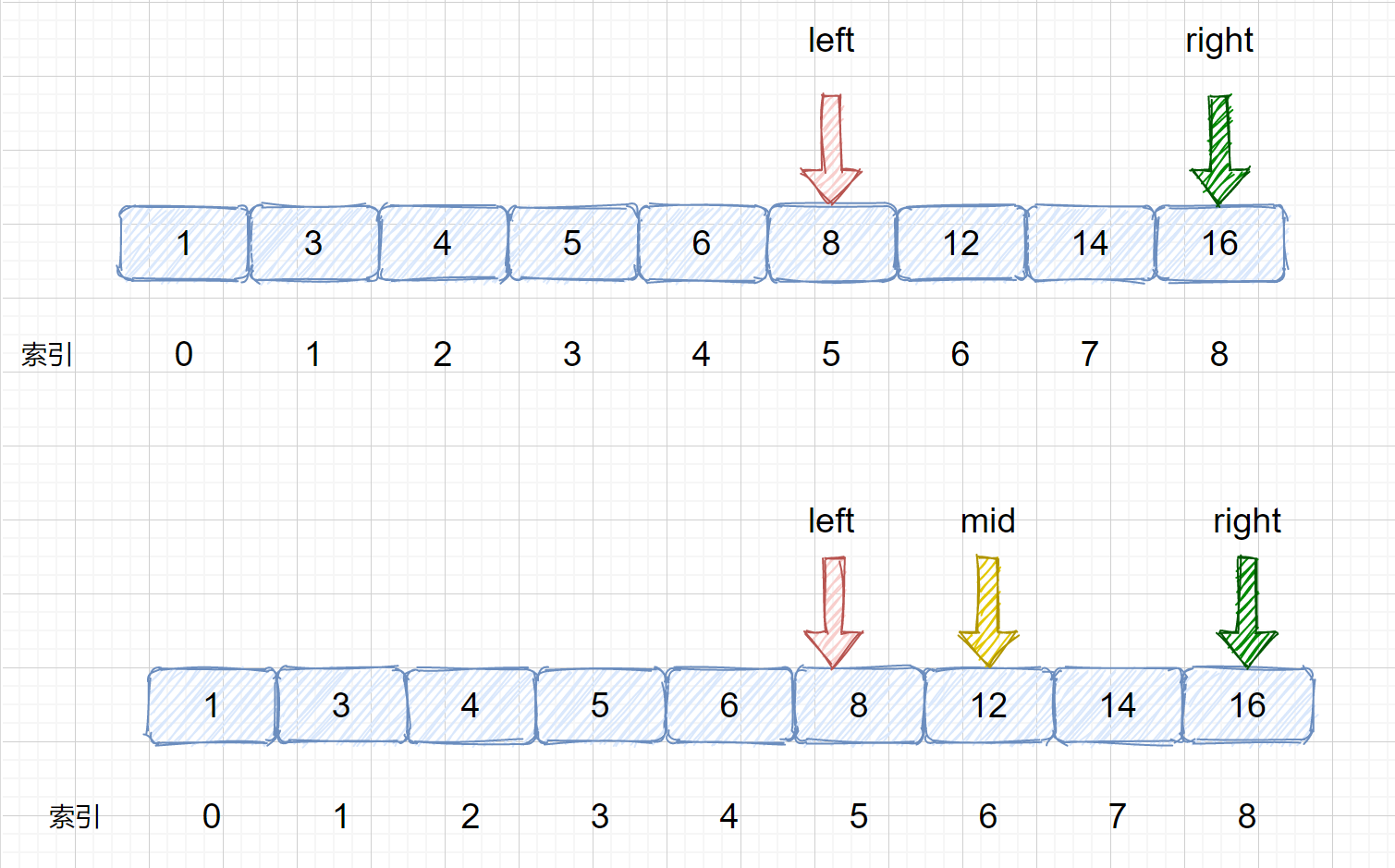
> 们需要在 left 和 right 之间计算 mid 值,`mid = 5 + (8 - 5)/ 2 = 6` 然后将` nums[mid]` 与
> `target `继续比较,进而决定下次移动left 指针还是 right 指针,见下图
> 
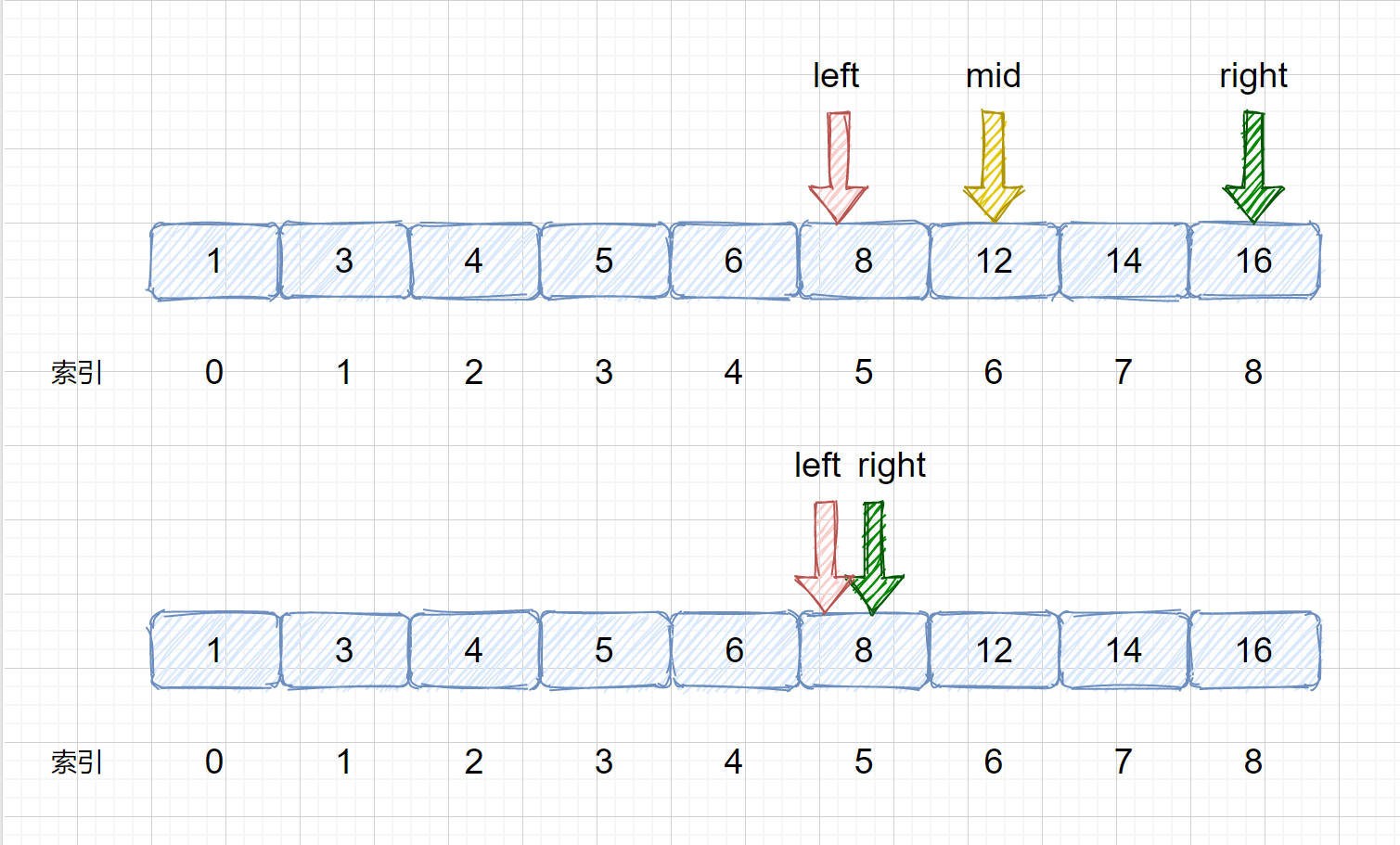
> 我们发现 `nums[mid] > target`,则需要移动我们的 right 指针, 则 `right = mid - 1`;则移动过后我们的 left 和 right 会重合,这里是我们的一个重点大家需要注意一下,后面会对此做详细叙述。
> 
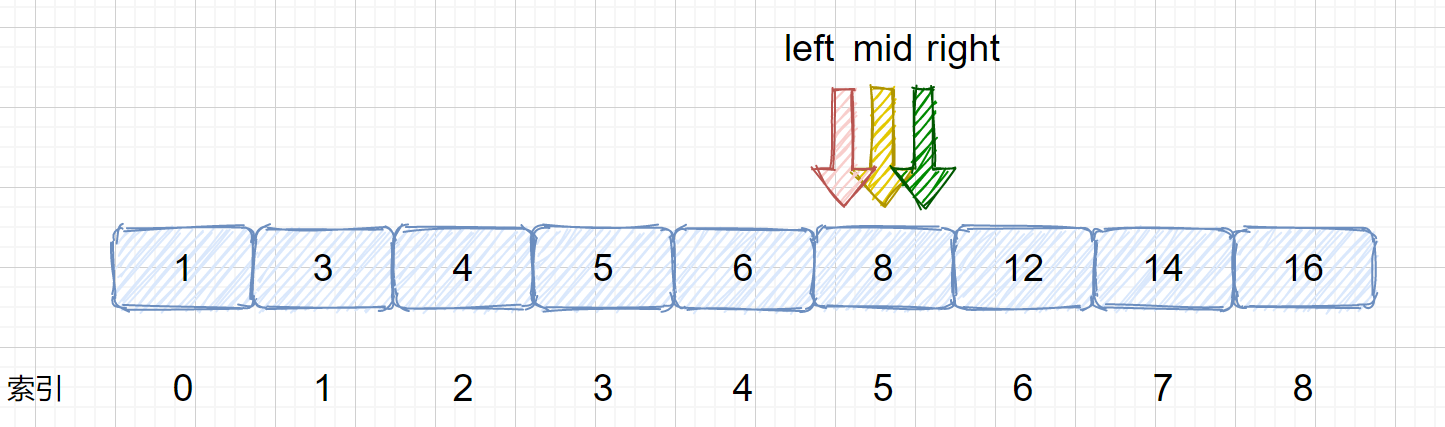
> 我们需要在 left 和 right 之间继续计算 mid 值,则 `mid = 5 +(5 - 5)/ 2 = 5` ,见下图,此时我们将 `nums[mid]` 和 `target` 比较,则发现两值相等,返回 mid 即可 ,如果不相等则跳出循环,返回 -1。
> 
> **动图解析:**
> 
```javascript
//这里需要注意,循环条件
while (left <= right) {
//这里需要注意,计算mid
int mid = left + ((right - left) >> 1);
if (nums[mid] == target) {
return mid;
}else if (nums[mid] < target) {
//这里需要注意,移动左指针
left = mid + 1;
}else if (nums[mid] > target) {
//这里需要注意,移动右指针
right = mid - 1;
}
}
//没有找到该元素,返回 -1
return -1;
2.查找数组中目标值的第一个索引和最后一个索引
题解:
此时 mid = 4 ,nums[mid] = 5,但是此时的 mid 指向的并不是第一个 5,所以我们需要继续查找 ,因为我们要找的是数的下边界,所以我们需要在 mid 的值的左区间继续寻找 5 ,那我们应该怎么做呢?我们只需在
target <= nums[mid]时,让right = mid - 1即可,这样我们就可以继续在 mid 的左区间继续找 5 。是不是听着有点绕,我们通过下面这组图进行描述。其实原理很简单,就是我们将小于和等于合并在一起处理,当 target <= nums[mid] 时,我们都移动右指针,也就是 right = mid -1,还有一个需要注意的就是,我们计算下边界时最后的返回值为 left ,当上图结束循环时,left = 3,right = 2,返回 left 刚好时我们的下边界。我们来看一下求下边界的具体执行过程。
计算上边界时算是和计算上边界时条件相反, 计算下边界时,当 target <= nums[mid] 时,right = mid -1;target > nums[mid] 时,left = mid + 1; 计算上边界时,当 target < nums[mid] 时,right = mid -1; target >= nums[mid] 时 left = mid + 1;刚好和计算下边界时条件相反,返回right。
var searchRange = function(nums, target) {
if(upper(nums, target) < lower(nums, target)){
return [-1,-1]
}
return [lower(nums, target),upper(nums, target)]
};
let lower = function(nums, target){
let left = 0,right = nums.length -1
while(left<=right){
let mid = left+((right-left)>>1)
if(nums[mid] >= target){
right = mid -1
}else{
left = mid + 1
}
}
return left
}
let upper = function(nums, target){
let left = 0 ,right = nums.length-1
while(left<=right){
let mid = left+((right-left)>>1)
if(nums[mid] <= target){
left = mid + 1
}else{
right = mid -1
}
}
return right
}
35.搜索插入位置
81搜索旋转排序数组2
73寻找旋转排序数组的最小值
74搜索二维矩阵


