二叉树

一、基本的概念

节点：就是图中的1,2,3,4,5,6,7,8
节点的度：一个节点的孩子节点数。
树的度：他的节点的度数最高的度数。
叶子节点：没有孩子节点的节点。
分支节点：有孩子节点的节点。
内部节点：非叶子节点，非根节点。
父节点，子节点，这两个概念是相对的。
兄弟节点：同一个父节点，也包括堂兄弟节点
层次：上图中表示的层数。
平衡因子：左子树高度和右子树高度的差值。

二、特殊的二叉树

1，满二叉树：没有缺失的部分，他的节点的度为0/2

2，完全二叉树：除了最下面一层，上面的层都是满的树，最下面一层的节点是从左到右连续排列的（中间不能间断，间断的二叉树不能称之为完全二叉树）。

3，非完全二叉树：不符合完全二叉树的条件的树

4，二叉搜索树：左孩子的值<父节点的值<右孩子的值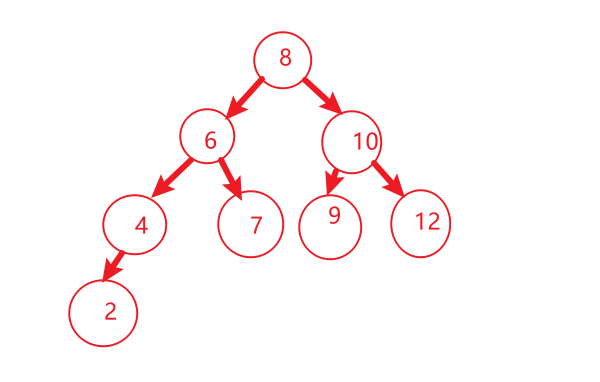

5,平衡二叉搜索树：左子树和右子树高度差不大于1

三、遍历二叉树

1. 递归遍历
2. 非递归遍历

   四、例题

   1.中序后继

   var inorderSuccessor = function(root, p) {
   const stack = [];
   let prev = null, curr = root;
   while (stack.length || curr) {
    while (curr) {
      stack.push(curr);
      curr = curr.left;
    }
    curr = stack.pop();
    if (prev === p) {
      return curr;
    }
    prev = curr;
    curr = curr.right;
   }
   return null;
   };

   2.二叉树展开为链表

   var flatten = function (root) {
   let list = []
   prevOrder(root, list)
   for (let i = 1; i < list.length; i++) {
    prev = list[i - 1],
    cur = list[i]
    prev.left = null
    prev.right = cur
   }
   };
   // 前序遍历
   var prevOrder = function (root, list) {
   if (root) {
    list.push(root)
    prevOrder(root.left, list)
    prevOrder(root.right, list)
   }
   }

   3.翻转二叉树

   var invertTree = function(root) {
   if(root){
        const temp = root.right;
        root.right = root.left;
        root.left = temp;
        invertTree(root.right);
        invertTree(root.left);
        return root
    }
    return root
   };