什么是回溯算法

回溯算法，又称为“试探法”。解决问题时，每进行一步，都是抱着试试看的态度，如果发现当前选择并不是最好的，或者这么走下去肯定达不到目标，立刻做回退操作重新选择。这种走不通就回退再走的方法就是回溯算法。回溯算法本质上是一种穷举算法，属于暴力搜索算法的一种。它虽然可以使用剪枝进行优化，仍不高效，但却实用。它往往能够解决可以抽象成树形结构的问题，亦可以认为是使用 K 层 for循环实现搜索的问题

回溯算法是一种暴力的搜索方法

回溯算法针对的问题

1.组合问题

按一定规则在 N 个数中找出 K 个数的集合

2.切割问题

一个字符串按一定规则切割成子串，求子串个数或符合条件的子集

3.子集问题

在N 个数的集合中，存在按一定规则分割出的符合某些条件的子集

4.排列问题

N 个数按一定规则全排列，求其排列结果

5.棋盘问题

N 皇后问题、数独问题、迷宫问题等等

注：组合与全排列最大的不同就是，子集划分是否强调元素顺序，强调顺序的为全排列，即组合只往后看，排列前后都要看，可从下图清晰观察到两者的差别。

  • 排列每层都是从 0 开始
  • 排列需要 used 数组记录元素是否使用过，一个排列中元素只能使用一次

在回溯算法中，我们需要清楚以下几种规则即可：

  • 使用回溯算法前，可先将问题转化为树形结构
  • 回溯算法解决问题都是在集合中递归子集，即常常以递归为基础实现的
  • 回溯算法基本可以抽象成一颗 N 叉树形式的问题树，其宽度为集合大小，递归（纵向遍历）深度为树的深度
  • 回溯算法常常使用 for 循环来遍历集合区间，即层次（横向）遍历问题树
  • 回溯算法解决的问题结果常常在叶子结点之上
  • 回溯算法需要考虑集合内元素是否可以重复选取，要求不同，方案不同
  • 回溯算法常常使用布尔数组（used）来进行去重工作，必须先对目标集合（存在重复元素）进行排序才能去重
    • 树层去重：子集内可重复，子集间不可重复
    • 树枝去重：子集内不可重复，子集间可重复
  • 回溯算法剪枝优化常常从可获取的子集中剩余元素条件与要求元素条件相比较，不符合就剪枝
  • 回溯算法如果在递归函数调用前，对全局变量有所调整，必须在递归函数后添加撤销语句

回溯法需要图形化树形结构，抽象成N叉树，树的宽度就是处理的集合的大小。

回溯法的模板

在了解到回溯算法的几项规则之后，再提供一套回溯算法的模板，如下：

  1. 确定回溯算法的返回值和相关参数
    • 返回值一般为 void ，最终结果常常定义为全局参数
    • 相关参数将会与回溯递归函数的相关参数一致，以递归要求为依据确定
  2. 确定回溯递归函数的终止条件
    • 注意剪枝判断在递归终止判断之前
    • 递归一定需要终止，即纵向遍历终止条件
    • 终止就意味着满足了题目要求的条件存储结果，或者剪枝去除提高效率
  3. 确定单层遍历的过程
    • 单层遍历即横向遍历，需要注意两个点，for 循环起始点及终止点，必须保证遍历完全
    • 起始点与集合大小、是否可重复选取、是否需要去重、是否为排列问题、是否为组合问题等等有关
    • 终止点与集合大小、剪枝条件等等

      回溯算法的关键

      回溯算法的关键是确定递归的出口，并将问题抽象成二叉树。
  1. // 简单模版
  2. function backtrack(nums){
  3.   let res = [];
  4.   let used = [];
  5.   let len = nums.length
  6.   function dfs(depth, path = []){ // depth表示当前所在的阶段
  7.     // 递归终止条件
  8.     if(depth === len){
  9.       res.push(path);
  10.       return;
  11.     }
  13.     // 针对当前depth尝试所有可能的结果
  14.     for(let i=0; i<len; i++){
  15.       if(!used[i]){ // 此路不通的标记
  16.         path.push(nums[i]);
  17.         used[i] = true;
  19.         // depth+1 前往下一个阶段
  20.         dfs(depth+1, path);
  22.         // 重置本阶段状态，尝试本阶段的其他可能
  23.         used[i] = false;
  24.         // 回溯到上一个阶段
  25.         path.pop();
  26.       }
  27.     }
  28.   }
  29.   //dfs初始化调用
  30.   dfs(0,0)
  31. }

全排列问题

题解：

  1. var permute = function(nums) {
  2. let res = []
  3. let n = nums.length
  4. let used = new Array(n).fill(false)
  5. function dfs(depth,path=[]){
  6.   if(depth === n){
  7.     // 浅拷贝一个数组用来存储，不能直接push path数组，否则返回的是空数组
  8.     res.push(Array.from(path))
  9.     // 或者res.push(path.slice())
  10.     return
  11.   }
  12.   for(let i =0;i<n;i++){
  13.     if(!used[i]){
  14.       path.push(nums[i])
  15.       used[i] = true
  16.       dfs(depth+1,path)
  17.       used[i] = false
  18.       path.pop()
  19.     }
  20.   }
  21. }
  22. dfs(0,[])
  23. return res
  24. };

火柴拼正方形

题解：

  1. let makesquare = (nums) => {
  2.   if(nums.length<4)return false
  3.   let total = nums.reduce((i,x)=>x+=i)
  4.   if(total%4)return false
  5.   nums.sort((a,b)=>b-a)
  6.   const SIDE = total/4
  7.   if(nums[0]>SIDE)return false
  8.   let edges = [0,0,0,0]
  9.   // 回溯
  10.   const dfs = (i) => {
  11.     if(i === nums.length)return true
  12.     for(let k = 0;k<4;k++){
  13.       // 剪枝
  14.       if(edges[k] + nums[i] > SIDE || (k && edges[k]===edges[k-1]))continue
  15.       edges[k] += nums[i] 
  16.       if(dfs(i+1))return true
  17.       edges[k] -= nums[i]
  18.     }
  19.     return false
  20.   }
  21.   return dfs(0)
  22. }

组合总和问题

image.png
解析：

  • ×：当前组合和之前生成的组合重复了。
  • △：当前求和 > target，不能选下去了，返回。
  • ○：求和正好 == target，加入解集，并返回。

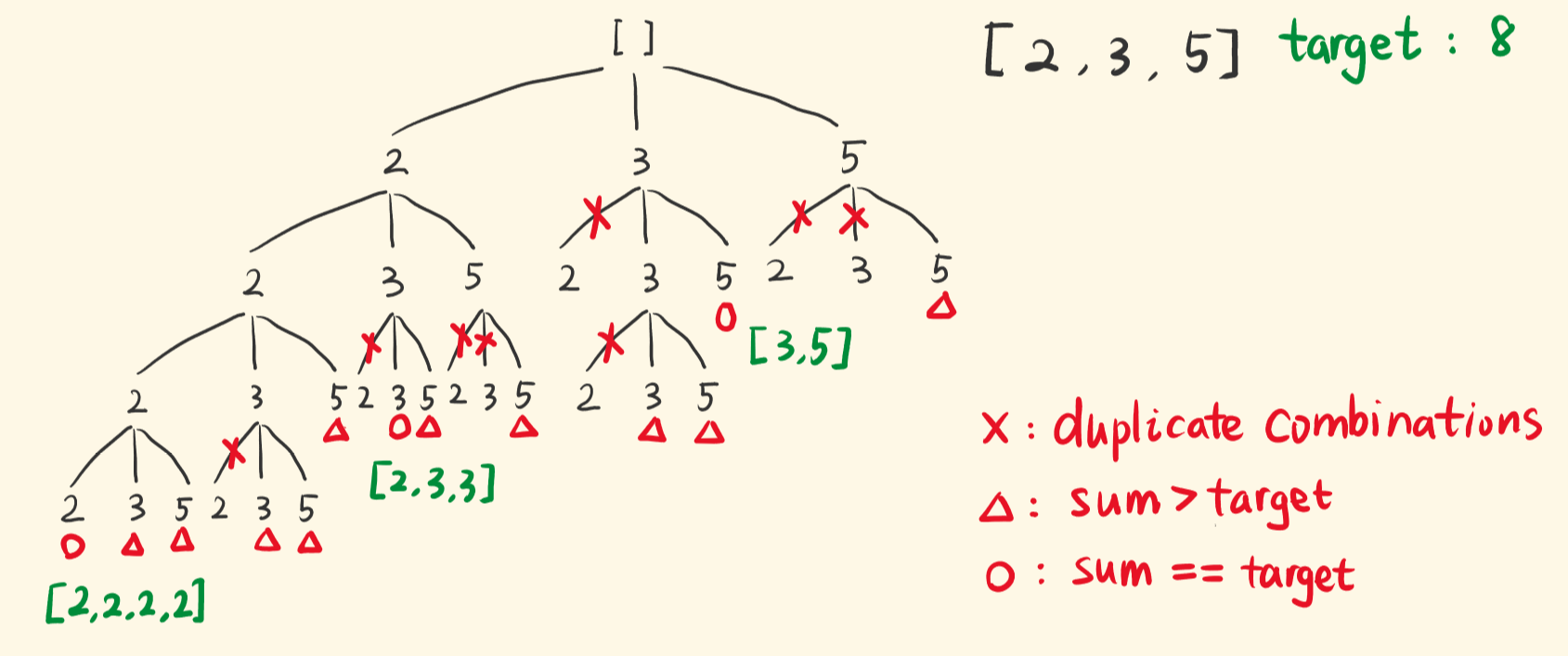
回溯算法 - 图2
不产生重复组合怎么限制（剪枝）？
如图，只要限制下一次选择的起点，是基于本次的选择，这样下一次就不会选到本次选择同层左边的数。即通过控制 for 遍历的起点，去掉会产生重复组合的选项。

注意，子递归传了 i 而不是 i+1 ，因为元素可以重复选入集合，如果传 i+1 就不重复了。

  1. for (let i = start; i < candidates.length; i++) { // 枚举当前可选的数，从start开始
  2.     temp.push(candidates[i]);          // 选这个数
  3.     dfs(i, temp, sum + candidates[i]); // 基于此，继续选择，传i，下次就不会选到i左边的数
  4.     temp.pop();   // 撤销选择，回到选择candidates[i]之前的状态，继续尝试选同层右边的数
  5. }

题解：

  1. const combinationSum = (candidates, target) => {
  2.   const res = [];
  3.   const dfs = (start, temp, sum) => { 
  4.     // start是当前选择的起点索引 temp是当前的集合 sum是当前求和
  5.     if (sum >= target) {
  6.       if (sum == target) {
  7.         res.push(temp.slice()); // temp的拷贝 加入解集
  8.       }
  9.       return;   // 结束当前递归
  10.     }
  11.     for (let i = start; i < candidates.length; i++) { // 枚举当前可选的数，从start开始
  12.       temp.push(candidates[i]);          // 选这个数
  13.       dfs(i, temp, sum + candidates[i]); // 基于此继续选择，传i，下一次就不会选到i左边的数
  14.       temp.pop();   // 撤销选择，回到选择candidates[i]之前的状态，继续尝试选同层右边的数
  15.     }
  16.   };
  17.   dfs(0, [], 0); // 最开始可选的数是从第0项开始的，传入一个空集合，sum也为0
  18.   return res;
  19. };