滑动窗口和前缀和适合连续的子问题。

滑动窗口

滑动窗口是一种解决问题的思路和方法，通常用来解决一些连续问题。
滑动窗口主要用来处理连续问题。比如题目求解“连续子串 xxxx”，“连续子数组 xxxx”，就应该可以想到滑动窗口。
从类型上说主要有：

  • 固定窗口大小
  • 窗口大小不固定，求解最大的满足条件的窗口
  • 窗口大小不固定，求解最小的满足条件的窗口

后面两种我们统称为可变窗口。当然不管是哪种类型基本的思路都是一样的，不一样的仅仅是代码细节。

固定窗口大小

对于固定窗口，我们只需要固定初始化左右指针 l 和 r，分别表示的窗口的左右顶点，并且保证：

  1. l 初始化为 0
  2. 初始化 r，使得 r - l + 1 等于窗口大小
  3. 同时移动 l 和 r
  4. 判断窗口内的连续元素是否满足题目限定的条件
    • 4.1 如果满足，再判断是否需要更新最优解，如果需要则更新最优解
    • 4.2 如果不满足，则继续。

滑动窗口和前缀和 - 图1

可变窗口大小

对于可变窗口，我们同样固定初始化左右指针 l 和 r，分别表示的窗口的左右顶点。后面有所不同，我们需要保证：

  1. l 和 r 都初始化为 0
  2. r 指针移动一步
  3. 判断窗口内的连续元素是否满足题目限定的条件
    • 3.1 如果满足，再判断是否需要更新最优解，如果需要则更新最优解。并尝试通过移动 l 指针缩小窗口大小。循环执行 3.1
    • 3.2 如果不满足，则继续。

形象地来看的话，就是 r 指针不停向右移动，l 指针仅仅在窗口满足条件之后才会移动，起到窗口收缩的效果。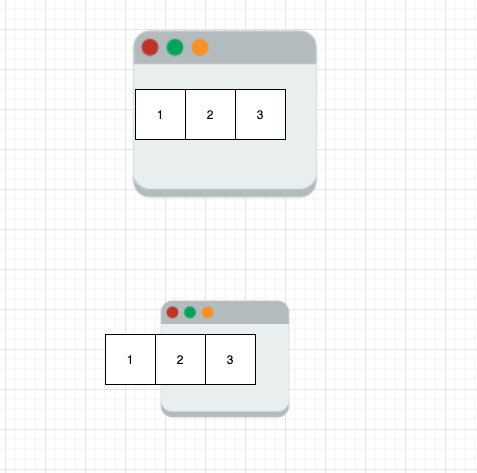
滑动窗口和前缀和 - 图2

模板代码

伪代码

  1. // 最长模板
  2. 初始化 left, right, result, bestResult
  3. while (右指针没有到达结尾) {
  4.   窗口扩大，加入right对应元素，更新当前result
  5.   while (result不满足要求) {
  6.     窗口缩小，移除left对应元素，left右移
  7.   }
  8.   更新最优结果bestResult
  9.   right++
  10. }
  11. 返回bestResult
  13. // 最短模板
  14. 初始化left，right，result，bestResult
  15. while (右指针没有到达结尾) {
  16.   窗口扩大，加入right对应元素，更新当前result
  17.   while (result满足要求) {
  18.     更新最优结果bestResult
  19.     窗口缩小，移除left对应元素，left右移
  20.   }
  21.   right++
  22. }
  23. 返回bestResult

例题1-最短超串

image.png
题解：

 var set = new Set(small)
    var window = {}, cnt = 0    // 窗口计数，cnt窗口内拥有的set里元素的个数
    var left = 0,right = -1, len = big.length + 1    // 窗口的左右边界，窗口的长度
    var res = []
    while(right < big.length){
        right++;
        // 对于当前元素，如果在set里，就把window里的数量加1
        if(set.has(big[right])){
            if(!window[big[right]]) {
              cnt++
           }
            window[big[right]] = window[big[right]] + 1 || 1  
        }
        // 如果窗口内有了所有set里的元素，则尝试缩小左边界
        while(cnt == set.size){
            // 如果窗口包含全部元素，则比较长度是否更短
            if(cnt == set.size && right-left+1 < len){
                len = right-left+1
                res[0] = left, res[1] = right
            }   
            // 如果big[left]是set里的值，则缩小左边界时让window里对应元素个数减少1
            if(set.has(big[left]) && (--window[big[left]] === 0)) {
              cnt--
            }
            left++
        }
    }
    return res

前缀和

前缀和的思路是这样的，对于一个给定的数组 nums，我们额外开辟一个 前缀和数组 进行预处理：

let n = nums.length;
// 前缀和数组
let preSum = new Array(n+1)
preSum[0] = 0;
for (let i = 0; i < n; i++){
    preSum[i + 1] = preSum[i] + nums[i];
}

nums[i..j]见下图：
滑动窗口和前缀和 - 图4
这个前缀和数组 preSum 的含义也很好理解，preSum[i] 就是 nums[0..i-1] 的和。那么如果我们想求 nums[i..j] 的和，只需要一步操作 preSum[j+1]-preSum[i] 即可，而不需要重新去遍历数组了。
回到这个子数组问题，我们想求有多少个子数组的和为 k，借助前缀和技巧很容易写出一个解法：

var subarraySum = function (nums, k) {
  let n = nums.length;
  // 构造前缀和
  let preSum = new Array(n + 1)
  preSum[0] = 0;
  for (let i = 0; i < n; i++) {
    preSum[i + 1] = preSum[i] + nums[i];
  }

  let ans = 0;
  // 穷举所有子数组
  for (let i = 1，; i <= n; i++)
    for (let j = 0; j < i; j++)
      // sum of nums[j..i-1]
      if (preSum[i] - preSum[j] == k)
        ans++;

  return ans;
};

image.png
这个解法的时间复杂度 O(N^2) 空间复杂度 O(N)，并不是最优的解法。不过通过这个解法理解了前缀和数组的工作原理之后，可以使用一些巧妙的办法把时间复杂度进一步降低。

二、优化解法

前面的解法有嵌套的 for 循环：

 for (let i = 1，; i <= n; i++)
    for (let j = 0; j < i; j++)
      // sum of nums[j..i-1]
      if (preSum[i] - preSum[j] == k)
        ans++;
 return ans;

第二层 for 循环在干嘛呢？翻译一下就是，在计算，有几个 j 能够使得 preSum[i] 和 preSum[j] 的差为 k。毎找到一个这样的 j，就把结果加一。
我们可以把 if 语句里的条件判断移项，这样写：

if (preSum[j] == preSum[i] - k)
    ans++;

优化的思路是：直接记录下有几个 preSum[j] 和 preSum[i] - k 相等，直接更新结果，就避免了内层的 for 循环。我们可以用哈希表，在记录前缀和的同时记录该前缀和出现的次数。

var subarraySum = function(nums, k) {
    const n = nums.length;
    const preSum = new Map();
    // 将元素和作为键，值用来存储次数
    preSum.set(0, 1);
    let ans = 0, sum0_i = 0;
    for (let i = 0; i < n; i++) {
        // 求当前元素前缀和pre[i]
        sum0_i += nums[i];
        // 想找到的前缀和pre[j - 1]
        const sum0_j = sum0_i - k;
        if (preSum.has(sum0_j)) { // 如果有sum0_j, 则j~i区间内存在和为k的数
            ans += preSum.get(sum0_j); // 结果+1
        }
        // 将前缀和存入Map中, 记录pre[i]出现次数
        preSum.set(sum0_i, (preSum.get(sum0_i) ?? 0) + 1)
    }
    return ans;
};

image.png

题目示例

1.寻找数组的中心索引

给定一个整数类型的数组 nums，请编写一个能够返回数组 “中心索引” 的方法。 我们是这样定义数组 中心索引 的：数组中心索引的左侧所有元素相加的和等于右侧所有元素相加的和。 如果数组不存在中心索引，那么我们应该返回 -1。如果数组有多个中心索引，那么我们应该返回最靠近左边的那一个。

示例 1：

输入：nums = [1, 7, 3, 6, 5, 6] 输出：3

解释：
索引 3 (nums[3] = 6) 的左侧数之和 (1 + 7 + 3 = 11)，与右侧数之和 (5 + 6 = 11) 相等。
同时, 3 也是第一个符合要求的中心索引。
示例 2：

输入：nums = [1, 2, 3]
输出：-1

解释：
数组中不存在满足此条件的中心索引。
先遍历一遍求出数组的和，然后第二次遍历时，直接进行对比左半部分和右半部分是否相同，如果相同则返回 true，不同则继续遍历。

题解

function pivotIndex(nums) {
  let total = nums.reduce((a, b) => a + b)
  let leftSum = 0
  for (let i = 0; i < nums.length; i++) {
    if (leftSum * 2 + nums[i] === total){
      return i
    }
    leftSum += nums[i]
  }
  return -1
}