常量

numpy内置了一些常量，常用的有：

  1. print(np.e) # 2.718281828459045
  2. print(np.pi) # 3.141592653589793

算术运算与通用函数

以以下数组作为演示：

  1. x=np.arange(10)

通过布尔值筛选

  1. x<5 # array([ True,  True,  True, True, True, False, False, False, False, False ])

算数运算

  1. np.sqrt(x) # 平方根
  2. np.abs(x) # 绝对值

三角函数

  1. np.sin(x)
  2. np.cos(x)

统计函数

  1. np.sum(x) # 求和, 输出 45
  2. np.mean(x) # 计算均值, 输出 4.5
  3. np.median(x) # 中位数, 输出 4.5
  4. np.std(x) # 标准差, 输出 2.8722813232690143
  5. np.var(x) # 方差, 输出 8.25
  1. x=np.arange(1, 10)
  2. np.cumsum(x) # 累计求和, 输出 array([ 1,  3,  6, 10, 15, 21, 28, 36, 45], dtype=int32)
  3. np.cumproduct(x) # 累计求积, 输出 array([ 1, 2, 6, 24, 120, 720, 5040, 40320, 362880], dtype=int32)
  4. np.corrcoef(x) # 相关系数, 输出 1.0

指数与对数函数

  1. # 指数与对数函数
  2. np.exp(x)
  3. np.log(x)
  4. np.log2(x)
  5. np.log10(x)

通过数组调用

某些函数也可直接使用数组调用:

  1. x.min() # 同np.min(x)
  2. x.max() # 同np.max(x)
  3. x.sum() # 同np.sum(x)

指定在某个轴上的运算

多维数组, 可以通过axis指定在某个轴上的运算：

  1. a=np.arange(16).reshape([4,4])
  2. b=a.min(axis=0) # 计算每列的最小值
  3. c=a.min(axis=1) # 计算每行的最小值
  5. print(a)
  6. print(b)
  7. print(c)

输出：

  1. [[ 0  1  2  3]
  2.  [ 4  5  6  7]
  3.  [ 8  9 10 11]
  4.  [12 13 14 15]]
  5. [0, 1, 2, 3]
  6. [ 0,  4,  8, 12]

矩阵运算

矩阵与标量运算

  1. a=np.arange(16).reshape([4,4])
  2. a+1
  3. a-1
  4. a*2
  5. a/2
  6. a**2

某些操作（例如 += 和 *=）会更直接更改被操作的矩阵数组而不会创建新矩阵数组。

  1. a += 3
  2. a *= 3

多维数组拷贝后运算

举例：

  1. a = np.array([[1,2,3],[4,5,6]])
  2. b = a[:]
  4. print(a)
  5. print(b)
  7. for i in range(a.shape[0]):
  8.     a[:, i] = a[:, i] - 2
  10. print(a)
  11. print(b)

输出：

  1. [[1 2 3]
  2.  [4 5 6]]
  3. [[1 2 3]
  4.  [4 5 6]]
  6. [[-1  0  3]
  7.  [ 2  3  6]]
  8. [[-1  0  3]
  9.  [ 2  3  6]]

可以看出，由于a是二维数组，b拷贝a后，每一项指向的还是b的每一项的引用，所以修改a后，b也随之改变。

如果是一维数组，每个值是基本数据类型，则不会出现这种情况：

  1. a = np.array([1,2,3])
  2. b = a[:]
  4. print(a)
  5. print(b)
  7. a = a - 2
  9. print(a)
  10. print(b)

输出：

  1. [1 2 3]
  2. [1 2 3]
  4. [-1  0  1]
  5. [1 2 3]

矩阵与矩阵运算

  1. a=np.arange(1,17).reshape(4,4)
  2. b=np.arange(1,17).reshape(4,4)

a 和 b 均为:

  1. array([[ 1,  2,  3,  4],
  2.        [ 5,  6,  7,  8],
  3.        [ 9, 10, 11, 12],
  4.        [13, 14, 15, 16]])

按元素运算

  1. a+b
  2. a-b
  3. a*b
  4. a/b

矩阵乘法（点乘运算）

  1. a@b # 或 a.dot(b)

输出:

  1. array([[ 90, 100, 110, 120],
  2.        [202, 228, 254, 280],
  3.        [314, 356, 398, 440],
  4.        [426, 484, 542, 600]])

比如 a@b 的 [0, 0] 元素为 1*1 + 2*5 + 3*9 + 4*13

原理如下:

📃 NumPy运算 - 图1
📃 NumPy运算 - 图2
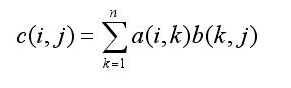
📃 NumPy运算 - 图3

根据线性代数的基础知识可知, 矩阵乘法 X@Y 只需要满足 X的列数 与 Y的行数 相等即可:

  1. a=np.arange(1,5).reshape(1,4)
  2. b=np.arange(5,9).reshape(4,1)
  3. a@b # 输出: array([70])

以上示例, 其实可以看做是 向量的点乘运算(数量积)

矩阵操作**

矩阵转置

  1. a = np.array([[1,2,3],[4,5,6]])
  2. b = a.transpose()
  4. print(a)
  5. print(b)

输出：

  1. [[1 2 3]
  2.  [4 5 6]]
  3. [[1 4]
  4.  [2 5]
  5.  [3 6]]

方阵的对角线元素

通过diag返回方阵（行列元素数量相同）的对角线元素

  1. a=np.arange(16).reshape([4,4])
  2. np.diag(a) # array([ 0,  5, 10, 15])

矩阵的迹

其实就是计算方阵对角线元素的和

  1. a=np.arange(12).reshape([3,4])
  2. a.trace() # 15

linalg

numpy.linalg 模块中的函数是满足行业标准级的Fortran库。

计算矩阵行列式

  1. a=np.arange(16).reshape([4,4])
  2. np.linalg.det(a)

计算逆矩阵

  1. a=np.arange(16).reshape([4,4])
  2. np.linalg.inv(a) # 或 np.linalg.solve(a, np.eye(4))

解线性方程组Ax=b

  1. a=np.arange(16).reshape([4,4])
  2. np.linalg.solve(a, np.eye(4)) # 此处求出的 x 即为 a的逆矩阵

计算方阵的本征值与本征向量

  1. a=np.arange(16).reshape([4,4])
  2. np.linalg.eig(a)