导数、偏导数、梯度
有关导数、偏导数、梯度的知识,可以先通过以下视频了解:
点击查看【bilibili】
一元函数的导数
导数定义:
或者:
对于一元函数来说,导数就是变化率、是切线的斜率。
左导数和右导数
函数在
处的左、右导数分别定义为:
左导数:
右导数:
在一元函数中,切线其实是可以向两个方向延伸的,但某些情况,曲线在某些点的切线只能沿某个方向延伸,几何意义如下: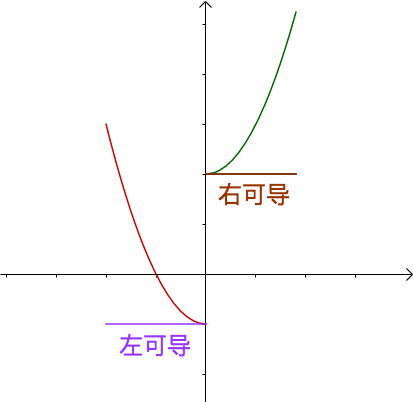
上图,射线可以类比左可导、右可导中的“左”和“右”,但在,在x=0这个点,此曲线(不连续)却是不可导的。
所以,当于左右导数相等,我们就称为此点可导。
平面曲线的切线和法线
切线方程 :
法线方程:
多元函数的导数
在二元函数(更多元的咱也画不出来)中,比如这样一个曲面上的一点:
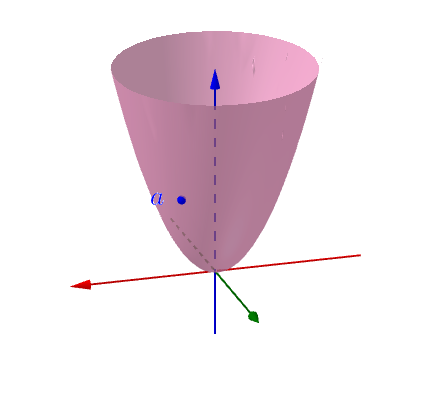
可以发现,一元函数的切线概念就不起效了,因为在这个点的每个方向上可以延伸出无数条切线: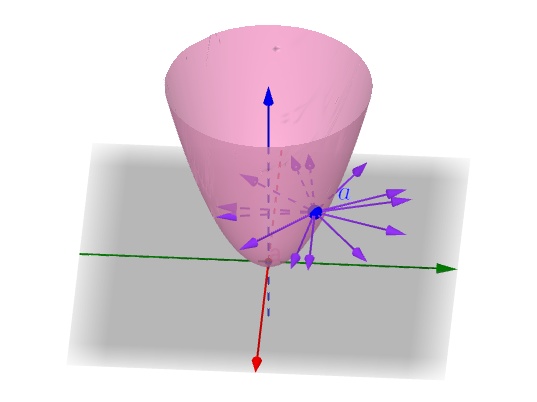
这些切线沿着每个方向延伸都是一个个向量,而这些向量是共面的,就是切面: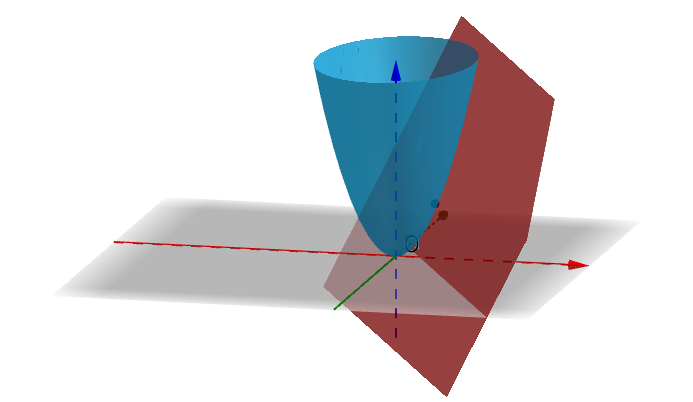
导数最主要的目的是找到“线性近似”,在一元函数的时候是要找到切线,在二元函数的时候是要找到一个切面。一个平面是没有斜率的概念的,因此我们不能把导数继续看作斜率了。
下面,需要引入向量和矩阵的相关知识。
首先,所有的肯定是共面的:
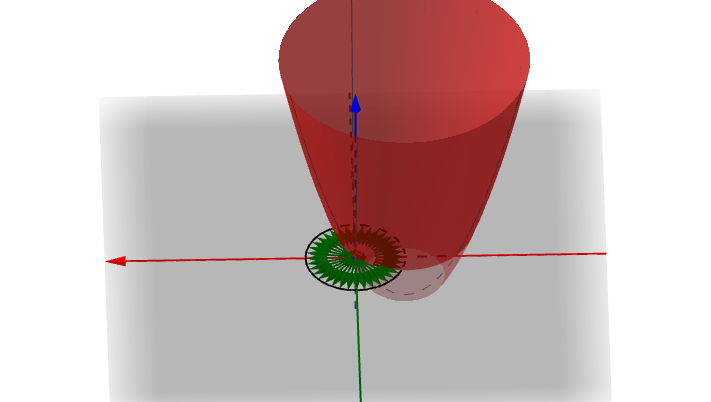
因为此点可导,即所有的的导数都是
,所以变换后的结果也共面(线性变换的特点是,变换前是共面的,变换后也是共面的):
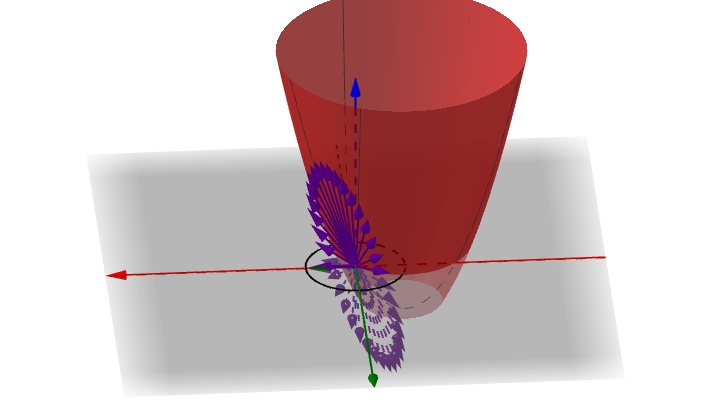
我们把这些 分别记为
,那它们的切线分别为:
其中, 都是矩阵,它们就是方向导数。
如果有 ,那么此点可导,此点导数即为
。
偏导数
偏导数写法举例:
对于多元函数,比如:
其对x的偏导数,可以将y看为常量,然后求导,就是:
其对y的偏导数,可以将x看为常量,然后求导,就是:
梯度
梯度可以定义为一个函数的全部偏导数构成的向量,比如三元函数:
比如上面所提到的函数,其梯度为:
梯度向量的方向是函数值变化率最大的方向。
上述函数,其在点处的梯度就为
函数的可导性与连续性之间的关系
1、函数在
处可微 ⇔
在
处可导
2、若函数在点处可导,则
在点
处连续,反之则不成立。即函数连续不一定可导。
3、**存在 ⇔
极限
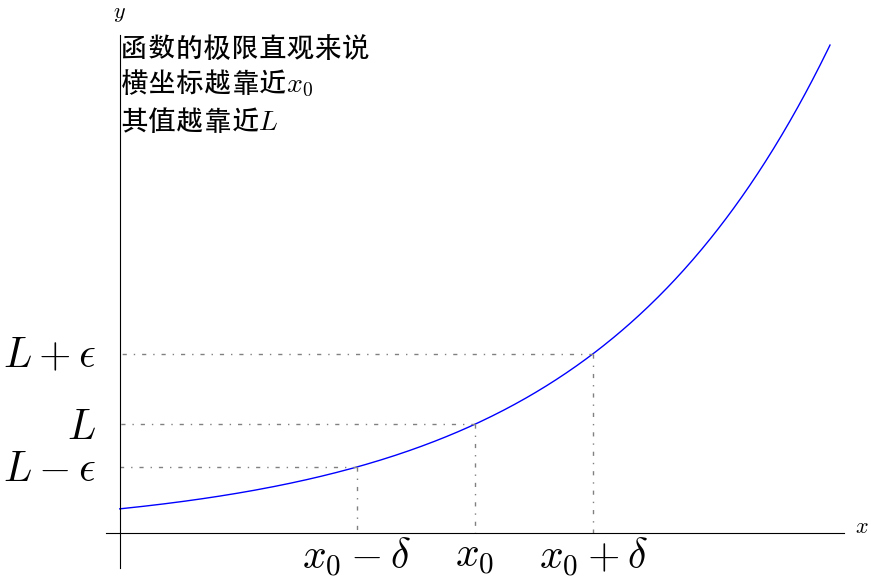
现在都是用 语言来描述极限:
微积分
古典微积分
导数的出现不是牛顿和莱布尼兹发明的,之前数学家已经在对曲线的切线进行研究了,但是牛顿和莱布尼兹在解决曲面下面积的时候把导数的定义确定下来了。
曲线下的面积在微积分出现之前是一个很复杂的问题,微积分求解的主要思想是把曲线下的面积划分成了无数个矩形面积之和: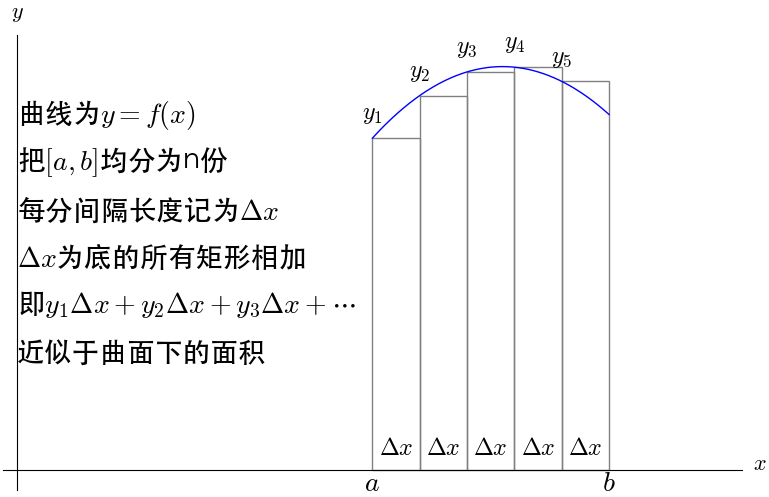
当n趋于无穷大,则曲线下的面积就等于这些矩形面积之和: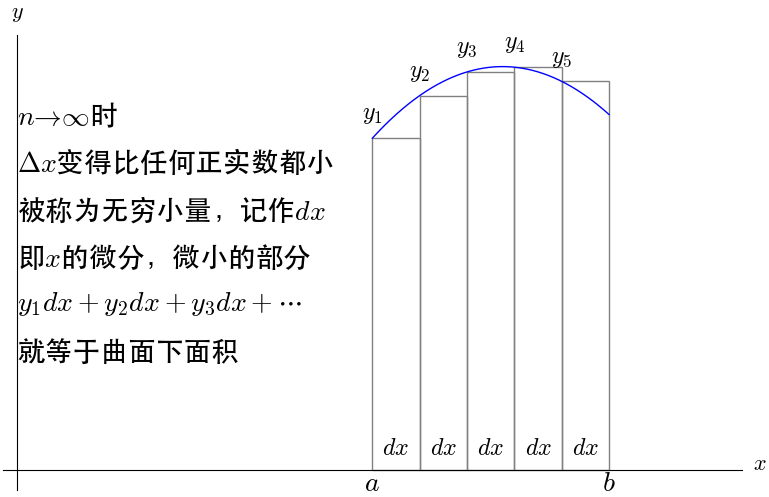
对于古典微积分的总结:
**
- 切线:通过无穷小量定义了切线
- 导数:导数就是切线的斜率
- 微分:微分是微小的增量,即无穷小量
极限微积分
**
导数的极限定义:
由导数的极限定义推到出微分的定义:
可以得出, 由两部分组成,通过图来观察一下其几何意义:
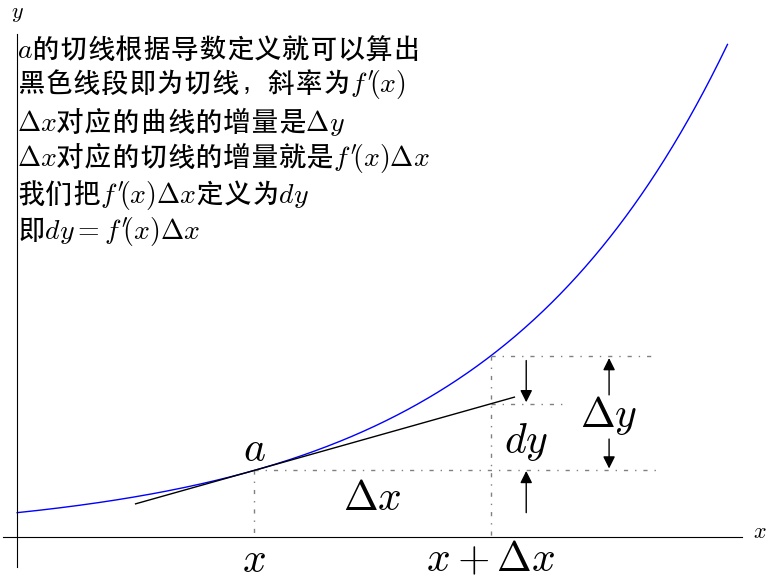
, 这个就是
的定义。
我们令 , 这个就是
的定义。
最后我们可以得到
对于极限微积分的总结
**
- 导数:被定义为一个极限,其意义就是变化率
- 微分:是一个线性函数,其意义就是变化的具体数值
- 切线:有了导数之后就可以被确定下来了
古典微积分与极限微积分的对比
- 古典微积分是先定义微分再定义导数,极限微积分是先定义导数再定义微分。
- 古典微积分的导数是基于无穷小量定义的,极限微积分的导数是基于极限定义的。
- 古典微积分的微分是无穷小量,极限微积分的微分是一个线性函数。
- 古典微积分的定积分是求无穷小矩形面积的和,极限微积分的定积分是求黎曼和。
- 古典微积分的切线是可以画出来的,极限微积分的切线是算出来的。
- 古典微积分的建立过程很直观,极限微积分的建立过程更抽象。
参考资料
导数相关
极限相关
微分相关

