波士顿房价预测

本文以经典的波士顿房价预测模型为例，展示使用NumPy进行模型训练的过程。

关于波士顿房价数据集的说明：

波士顿房价预测是一个经典的机器学习任务，类似于程序员世界的“Hello World”。和大家对房价的普遍认知相同，波士顿地区的房价是由诸多因素影响的。该数据集统计了13种可能影响房价的因素和该类型房屋的均价，期望构建一个基于13个因素进行房价预测的模型，如下图所示。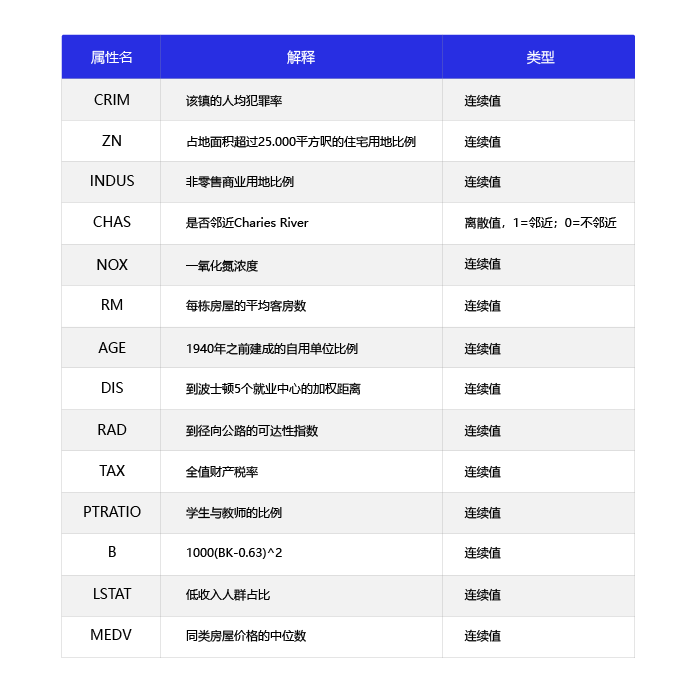
📃 使用NumPy做线性回归模型训练 - 图1
其数据集 housing.data 格式如下：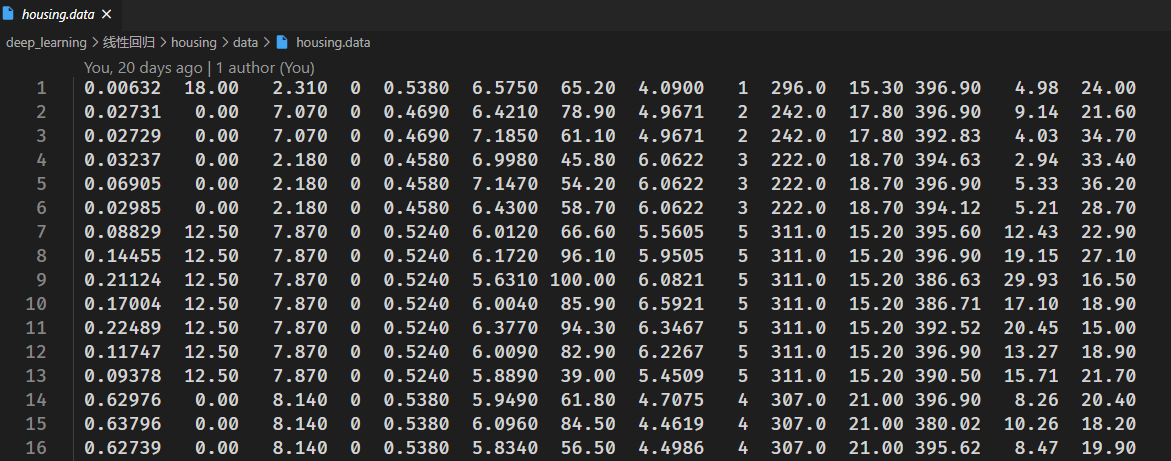
📃 使用NumPy做线性回归模型训练 - 图2
每一行的前13列是影响房价的13个因素（对应上表），最后一列是真实房价。

梯度下降

经典的四步训练流程：前向计算->计算损失->计算梯度->更新参数

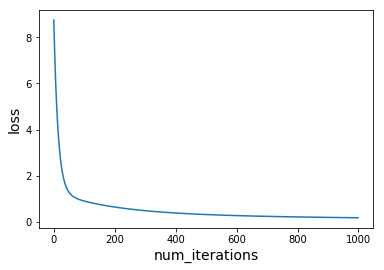
  1. # 导入需要用到的package
  2. import numpy as np
  3. import json
  5. # 使用matplotlib将两个变量和对应的Loss作3D图
  6. import matplotlib.pyplot as plt
  7. %matplotlib inline
  9. # 从文件导入数据
  10. def load_data(datafile):
  11.     data = np.fromfile(datafile, sep=' ')
  13.     # 每条数据包括14项，其中前面13项是影响因素，第14项是相应的房屋价格中位数
  14.     feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
  15.                       'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
  16.     feature_num = len(feature_names)
  18.     # 将原始数据进行Reshape，变成[N, 14]这样的形状
  19.     data = data.reshape([data.shape[0] // feature_num, feature_num])
  21.     # 将原数据集拆分成训练集和测试集
  22.     # 这里使用80%的数据做训练，20%的数据做测试
  23.     # 测试集和训练集必须是没有交集的
  24.     ratio = 0.8
  25.     offset = int(data.shape[0] * ratio)
  26.     training_data = data[:offset]
  28.     # 计算训练集的最大值，最小值，平均值
  29.     maximums = training_data.max(axis=0) # 指定 axis=0 计算每列的最大值
  30.     minimums = training_data.min(axis=0) # 指定 axis=0 计算每列的最小值
  31.     avgs = training_data.mean(axis=0) # 指定 axis=0 计算每列的平均值
  33.     # 对数据进行归一化处理
  34.     for i in range(feature_num):
  35.         data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
  37.     # 训练集和测试集的划分比例
  38.     training_data = data[:offset]
  39.     test_data = data[offset:]
  40.     return training_data, test_data
  42. class Network(object):
  43.     def __init__(self, num_of_weights):
  44.         # 随机产生w的初始值
  45.         # 为了保持程序每次运行结果的一致性，此处设置固定的随机数种子
  46.         np.random.seed(0)
  47.         self.w = np.random.randn(num_of_weights, 1)
  48.         self.b = 0.
  50.     # 前向计算
  51.     def forward(self, x):
  52.         return np.dot(x, self.w) + self.b
  54.     # 计算损失值，使用均方误差
  55.     def loss(self, z, y):
  56.         return np.sum((z - y) ** 2) / (z - y).shape[0]
  58.     # 计算梯度
  59.     def gradient(self, x, y):
  60.         z = self.forward(x)
  61.         gradient_w = np.mean((z-y)*x, axis=0)
  62.         gradient_w = gradient_w[:, np.newaxis] # 由于计算均值后，维度损失掉了，所以需要将损失的维度补足
  63.         gradient_b = np.mean(z - y)     
  64.         return gradient_w, gradient_b
  66.     # 更新参数
  67.     def update(self, gradient_w, gradient_b, eta = 0.01):
  68.         self.w = self.w - eta * gradient_w
  69.         self.b = self.b - eta * gradient_b
  71.     # 训练模型（梯度下降）
  72.     def train(self, train_data, iterations=100, eta=0.01):
  73.         x = train_data[:, :-1]
  74.         y = train_data[:, -1:]
  75.         losses = []
  76.         for i in range(iterations):
  77.             z = self.forward(x) #前向计算
  78.             L = self.loss(z, y) #计算损失
  79.             gradient_w, gradient_b = self.gradient(x, y) #计算梯度
  80.             self.update(gradient_w, gradient_b, eta) #更新参数
  81.             losses.append(L)
  82.             if (i+1) % 10 == 0:
  83.                 print('iter {}, loss {}'.format(i, L))
  84.         return losses
  86. # 获取数据
  87. train_data, test_data = load_data('./work/housing.data')
  89. # 创建网络
  90. net = Network(13) # 创建带13个参数的网络
  92. # 启动训练（梯度下降）
  93. losses = net.train(train_data, iterations=1000, eta=0.01)
  94. # 画出损失函数的变化趋势
  95. plot_x = np.arange(num_iterations)
  96. plot_y = np.array(losses)
  98. plt.xlabel("num_iterations", fontsize=14)
  99. plt.ylabel("loss", fontsize=14)
  101. plt.plot(plot_x, plot_y)
  102. plt.show()

训练输出：

  1. iter 9, loss 5.143394325795511
  2. iter 19, loss 3.097924194225988
  3. iter 29, loss 2.082241020617026
  4. iter 39, loss 1.5673801618157397
  5. iter 49, loss 1.2966204735077431
  6. iter 59, loss 1.1453399043319765
  7. iter 69, loss 1.0530155717435201
  8. iter 79, loss 0.9902292156463155
  9. iter 89, loss 0.9426576903842504
  10. iter 99, loss 0.9033048096880774
  11. ...
  12. iter 889, loss 0.19304908885621125
  13. iter 899, loss 0.1912555092527351
  14. iter 909, loss 0.1894982936296714
  15. iter 919, loss 0.18777618462820625
  16. iter 929, loss 0.18608798277314595
  17. iter 939, loss 0.18443254350353405
  18. iter 949, loss 0.18280877436103968
  19. iter 959, loss 0.18121563232764165
  20. iter 969, loss 0.17965212130459232
  21. iter 979, loss 0.1781172897250724
  22. iter 989, loss 0.1766102282933619
  23. iter 999, loss 0.17513006784373505

📃 使用NumPy做线性回归模型训练 - 图3

关于更新参数的说明

为了确定损失函数更小的点，更新参数时需要做以下操作：

  1.     def update(self, gradient_w, gradient_b, eta = 0.01):
  2.         self.w = self.w - eta * gradient_w
  3.         self.b = self.b - eta * gradient_b
  • 相减：参数需要向梯度的反方向移动，即斜率更小的反向。
  • eta：控制每次参数值沿着梯度反方向变动的大小，即每次移动的步长，又称为学习率。

随机梯度下降

  1. # 导入需要用到的package
  2. import numpy as np
  3. import json
  5. # 使用matplotlib将两个变量和对应的Loss作3D图
  6. import matplotlib.pyplot as plt
  7. %matplotlib inline
  9. # 从文件导入数据
  10. def load_data(datafile):
  11.     data = np.fromfile(datafile, sep=' ')
  13.     # 每条数据包括14项，其中前面13项是影响因素，第14项是相应的房屋价格中位数
  14.     feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
  15.                       'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
  16.     feature_num = len(feature_names)
  18.     # 将原始数据进行Reshape，变成[N, 14]这样的形状
  19.     data = data.reshape([data.shape[0] // feature_num, feature_num])
  21.     # 将原数据集拆分成训练集和测试集
  22.     # 这里使用80%的数据做训练，20%的数据做测试
  23.     # 测试集和训练集必须是没有交集的
  24.     ratio = 0.8
  25.     offset = int(data.shape[0] * ratio)
  26.     training_data = data[:offset]
  28.     # 计算训练集的最大值，最小值，平均值
  29.     maximums = training_data.max(axis=0) # 指定 axis=0 计算每列的最大值
  30.     minimums = training_data.min(axis=0) # 指定 axis=0 计算每列的最小值
  31.     avgs = training_data.mean(axis=0) # 指定 axis=0 计算每列的平均值
  33.     # 对数据进行归一化处理
  34.     for i in range(feature_num):
  35.         data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
  37.     # 训练集和测试集的划分比例
  38.     training_data = data[:offset]
  39.     test_data = data[offset:]
  40.     return training_data, test_data
  42. class Network(object):
  43.     def __init__(self, num_of_weights):
  44.         # 随机产生w的初始值
  45.         # 为了保持程序每次运行结果的一致性，此处设置固定的随机数种子
  46.         np.random.seed(0)
  47.         self.w = np.random.randn(num_of_weights, 1)
  48.         self.b = 0.
  50.     # 前向计算
  51.     def forward(self, x):
  52.         return np.dot(x, self.w) + self.b
  54.     # 计算损失值，使用均方误差
  55.     def loss(self, z, y):
  56.         return np.sum((z - y) ** 2) / (z - y).shape[0]
  58.     # 计算梯度
  59.     def gradient(self, x, y):
  60.         z = self.forward(x)
  61.         gradient_w = np.mean((z-y)*x, axis=0)
  62.         gradient_w = gradient_w[:, np.newaxis] # 由于计算均值后，维度损失掉了，所以需要将损失的维度补足
  63.         gradient_b = np.mean(z - y)     
  64.         return gradient_w, gradient_b
  66.     # 更新参数
  67.     def update(self, gradient_w, gradient_b, eta = 0.01):
  68.         self.w = self.w - eta * gradient_w
  69.         self.b = self.b - eta * gradient_b
  71.     # 训练模型（随机梯度下降）
  72.     def train(self, training_data, num_epoches, batch_size=10, eta=0.01):
  73.         n = len(training_data)
  74.         losses = []
  75.         for epoch_id in range(num_epoches):
  76.             # 在每轮迭代开始之前，将训练数据的顺序随机打乱
  77.             # 然后再按每次取batch_size条数据的方式取出
  78.             np.random.shuffle(training_data)
  79.             # 将训练数据进行拆分，每个mini_batch包含batch_size条的数据
  80.             mini_batches = [training_data[k:k+batch_size] for k in range(0, n, batch_size)]
  81.             for iter_id, mini_batch in enumerate(mini_batches):
  82.                 #print(self.w.shape)
  83.                 #print(self.b)
  84.                 x = mini_batch[:, :-1]
  85.                 y = mini_batch[:, -1:]
  86.                 a = self.forward(x) # 前向计算
  87.                 loss = self.loss(a, y) # 计算损失
  88.                 gradient_w, gradient_b = self.gradient(x, y) # 计算梯度
  89.                 self.update(gradient_w, gradient_b, eta) # 更新参数
  90.                 losses.append(loss)
  91.                 print('Epoch {:3d} / iter {:3d}, loss = {:.4f}'.
  92.                                  format(epoch_id, iter_id, loss))
  93.         return losses
  95. # 获取数据
  96. train_data, test_data = load_data('./work/housing.data')
  98. # 创建网络
  99. net = Network(13) # 创建带13个参数的网络
  101. # 启动训练（随机梯度下降）
  102. losses = net.train(train_data, num_epoches=50, batch_size=100, eta=0.1) # 随机梯度下降
  104. # 画出损失函数的变化趋势
  105. plot_x = np.arange(len(losses))
  106. plot_y = np.array(losses)
  107. plt.plot(plot_x, plot_y)
  108. plt.show()

训练输出：

  1. Epoch   0 / iter   0, loss = 10.1354
  2. Epoch   0 / iter   1, loss = 3.8290
  3. Epoch   0 / iter   2, loss = 1.9208
  4. Epoch   0 / iter   3, loss = 1.7740
  5. Epoch   0 / iter   4, loss = 0.3366
  6. Epoch   1 / iter   0, loss = 1.6275
  7. Epoch   1 / iter   1, loss = 0.9842
  8. Epoch   1 / iter   2, loss = 0.9121
  9. Epoch   1 / iter   3, loss = 0.9971
  10. Epoch   1 / iter   4, loss = 0.6071
  11. Epoch   2 / iter   0, loss = 0.7689
  12. Epoch   2 / iter   1, loss = 0.8547
  13. Epoch   2 / iter   2, loss = 0.9428
  14. Epoch   2 / iter   3, loss = 0.9791
  15. Epoch   2 / iter   4, loss = 0.4608
  16. ...
  17. Epoch  47 / iter   0, loss = 0.0896
  18. Epoch  47 / iter   1, loss = 0.0863
  19. Epoch  47 / iter   2, loss = 0.0933
  20. Epoch  47 / iter   3, loss = 0.0753
  21. Epoch  47 / iter   4, loss = 0.0106
  22. Epoch  48 / iter   0, loss = 0.0644
  23. Epoch  48 / iter   1, loss = 0.1005
  24. Epoch  48 / iter   2, loss = 0.0685
  25. Epoch  48 / iter   3, loss = 0.0836
  26. Epoch  48 / iter   4, loss = 0.1913
  27. Epoch  49 / iter   0, loss = 0.0898
  28. Epoch  49 / iter   1, loss = 0.0617
  29. Epoch  49 / iter   2, loss = 0.0771
  30. Epoch  49 / iter   3, loss = 0.0891
  31. Epoch  49 / iter   4, loss = 0.0369

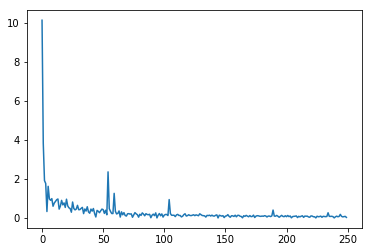
📃 使用NumPy做线性回归模型训练 - 图4
可以看出，跟普通梯度下降相比，随机梯度下降加快了训练过程，但由于每次仅基于少量样本更新参数和计算损失，所以损失下降曲线会出现震荡。