📃 实现神经网络的基本方法

构建神经网络/深度学习模型的基本步骤

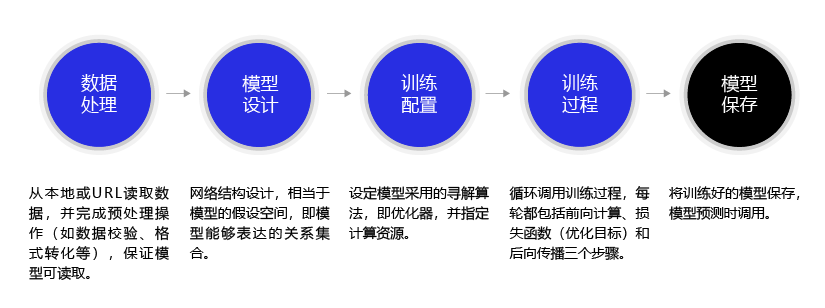
“横纵式”教学法

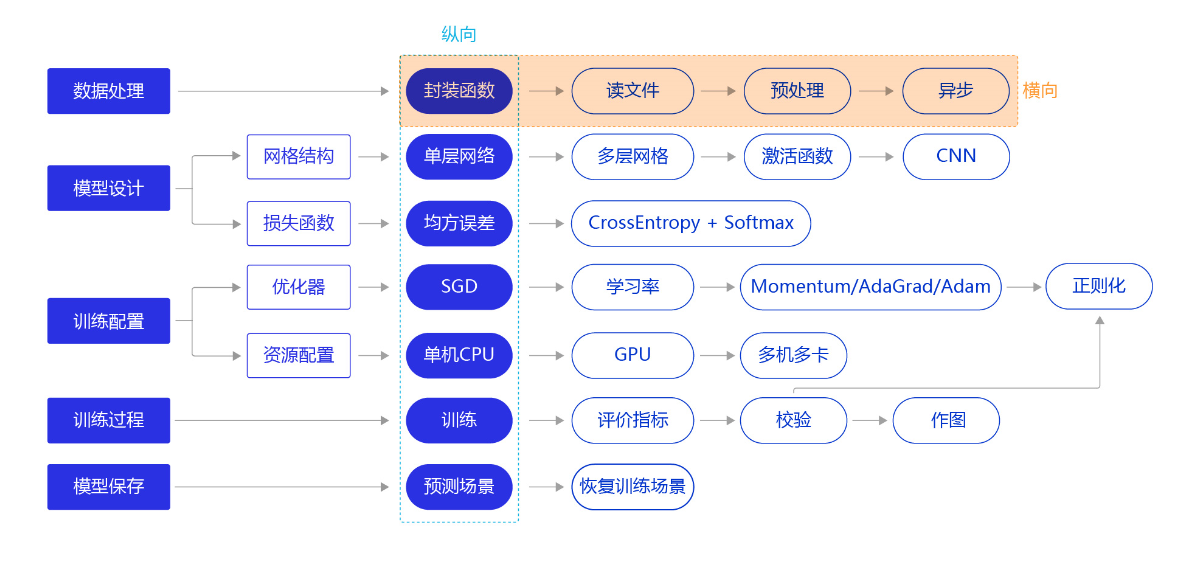
创新性的“横纵式”教学法

在“横纵式”教学法中，纵向概要介绍模型的基本代码结构和极简实现方案。横向深入探讨构建模型的每个环节中，更优但相对复杂的实现方案。例如在模型设计环节，除了在极简版本使用的单层神经网络外，还可以尝试更复杂的网络结构，如多层神经网络、加入非线性的激活函数，甚至专门针对视觉任务优化的卷积神经网络。

这种“横纵式”教学法的设计思路尤其适用于深度学习的初学者，具有如下两点优势：

• 帮助读者轻松掌握深度学习内容：采用这种方式设计教学案例，读者在学习过程中接收到的信息是线性增长的，在难度上不会有阶跃式的提高。
• 模拟真实建模的实战体验：先使用熟悉的模型构建一个可用但不够出色的基础版本（Baseline），再逐渐分析每个建模环节可优化的点，一点点的提升优化效果，让读者获得到真实建模的实战体验。

数据处理

数据集划分

在实际应用中，保存到本地的数据存储格式多种多样，以MNIST数据集为例，其数据存储结构如下图所示。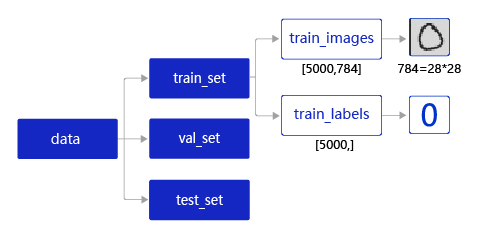

data包含三个元素的列表：train_set、val_set、 test_set。

• train_set（训练集）：包含50000条手写数字图片和对应的标签，用于确定模型参数。
• val_set（验证集）：包含10000条手写数字图片和对应的标签，用于调节模型超参数（如多个网络结构、正则化权重的最优选择）。
• test_set（测试集）：包含10000条手写数字图片和对应的标签，用于估计应用效果（没有在模型中应用过的数据，更贴近模型在真实场景应用的效果）。

train_set包含两个元素的列表：train_images、train_labels。

• train_images：[50000, 784]的二维列表，包含5000张图片。每张图片用一个长度为784的向量表示，内容是28*28尺寸的像素灰度值（黑白图片）。
• train_labels：[50000, ]的列表，表示这些图片对应的分类标签，即0-9之间的一个数字。

每个数据集的数据类型不尽相同，需要分析后进行处理。通常我们会将数据拆分为train（训练集）、valid（验证集）、test（测试集） 三个集合。

数据归一化处理

对每个特征进行归一化处理，使得每个特征的取值缩放到0~1之间。这样做有两个好处：一是模型训练更高效；二是特征前的权重大小可以代表该变量对预测结果的贡献度（因为每个特征值本身的范围相同）。

特征输入归一化后，不同参数输出的Loss是一个比较规整的曲线，学习率可以设置成统一的值 ；特征输入未归一化时，不同特征对应的参数所需的步长不一致，尺度较大的参数需要大步长，尺寸较小的参数需要小步长，导致无法设置统一的学习率。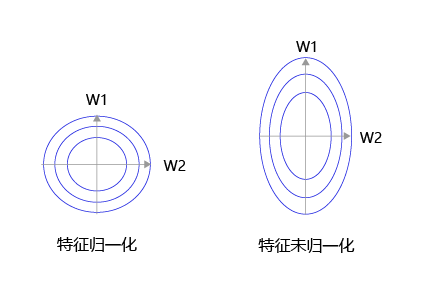

训练样本乱序、生成批次数据

训练样本乱序的目的：通过大量实验发现，模型对最后出现的数据印象更加深刻。训练数据导入后，越接近模型训练结束，最后几个批次数据对模型参数的影响越大。为了避免模型记忆影响训练效果，需要进行样本乱序操作。

• 训练样本乱序： 先将样本按顺序进行编号，建立ID集合index_list。然后将index_list乱序，最后按乱序后的顺序读取数据。
• 生成批次数据： 先设置合理的batch_size，再将数据转变成符合模型输入要求的np.array格式返回。同时，在返回数据时将Python生成器设置为yield模式，以减少内存占用。

校验数据有效性

在实际应用中，原始数据可能存在标注不准确、数据杂乱或格式不统一等情况。因此在完成数据处理流程后，还需要进行数据校验，一般有两种方式：

• 机器校验：加入一些校验和清理数据的操作。
• 人工校验：先打印数据输出结果，观察是否是设置的格式。再从训练的结果验证数据处理和读取的有效性。

异步数据读取

对于样本量较大、数据读取较慢的场景，建议采用异步数据读取方式。异步读取数据时，数据读取和模型训练并行执行，从而加快了数据读取速度，牺牲一小部分内存换取数据读取效率的提升，二者关系如下图所示。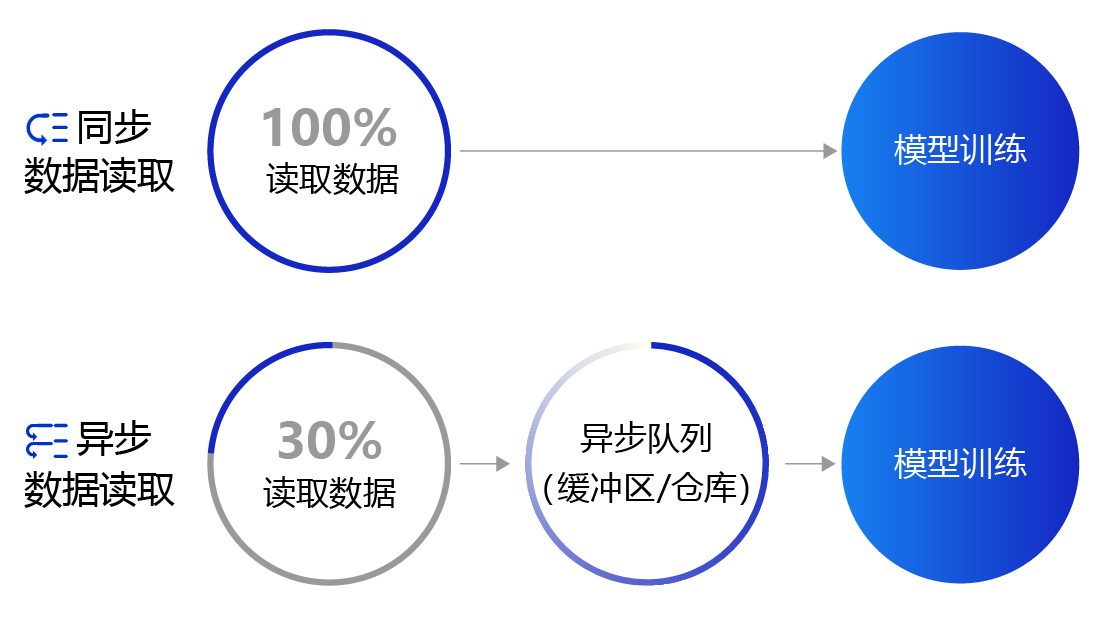

• 同步数据读取：数据读取与模型训练串行。当模型需要数据时，才运行数据读取函数获得当前批次的数据。在读取数据期间，模型一直等待数据读取结束才进行训练，数据读取速度相对较慢。
• 异步数据读取：数据读取和模型训练并行。读取到的数据不断的放入缓存区，无需等待模型训练就可以启动下一轮数据读取。当模型训练完一个批次后，不用等待数据读取过程，直接从缓存区获得下一批次数据进行训练，从而加快了数据读取速度。
• 异步队列：数据读取和模型训练交互的仓库，二者均可以从仓库中读取数据，它的存在使得两者的工作节奏可以解耦。

异步读取数据只在数据量规模巨大时会带来显著的性能提升，对于多数场景采用同步数据读取的方式已经足够。

模型设计

激活函数

非线性激活函数的目的是为了增加神经网络的非线性能力。

Sigmoid

Sigmoid是早期神经网络模型中常见的非线性变换函数，其图像如下：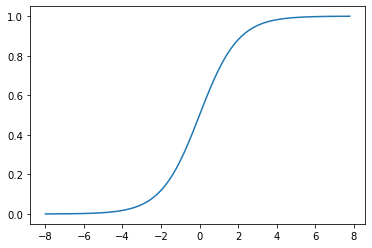

Softmax

如果模型能输出10个标签的概率，对应真实标签的概率输出尽可能接近100%，而其他标签的概率输出尽可能接近0%，且所有输出概率之和为1。这是一种更合理的假设！与此对应，真实的标签值可以转变成一个10维度的one-hot向量，在对应数字的位置上为1，其余位置为0，比如标签“6”可以转变成[0,0,0,0,0,1,0,0,0,0]。

为了实现上述思路，需要引入Softmax函数，它可以将原始输出转变成对应标签的概率，公式如下，其中C是标签类别个数。

从公式的形式可见，每个输出的范围均在0~1之间，且所有输出之和等于1，这是这种变换后可被解释成概率的基本前提。对应到代码上，我们需要在网络定义部分修改输出层：self.fc = Linear(input_dim=10, output_dim=1, act='softmax')，即是对全连接层的输出加一个softmax运算。

下图是一个三个标签的分类模型（三分类）使用的softmax输出层，从中可见原始输出的三个数字3、1、-3，经过softmax层后转变成加和为1的三个概率值0.88、0.12、0。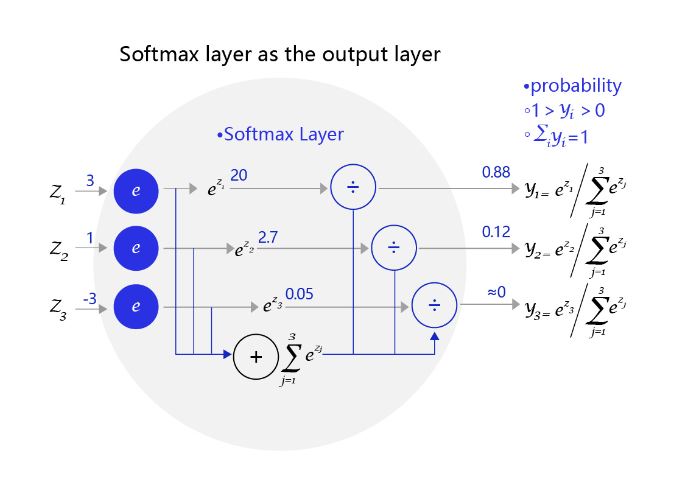

损失函数

损失函数是模型优化的目标，用于在众多的参数取值中，识别最理想的取值。损失函数的计算在训练过程的代码中，每一轮模型训练的过程都相同，分如下三步：

1. 先根据输入数据正向计算预测输出。
2. 再根据预测值和真实值计算损失。
3. 最后根据损失反向传播梯度并更新参数。

均方误差

均方误差（square_error_cost）计算公式：

在回归问题中，采用均方误差是一种比较常见的形式。

因为计算损失函数时需要把每个样本的损失函数值都考虑到，所以我们需要对单个样本的损失函数进行求和，并除以样本总数。

交叉熵

在模型输出为分类标签的概率时，直接以标签和概率做比较也不够合理，人们更习惯使用交叉熵（cross_entropy）误差作为分类问题的损失衡量。

交叉熵的公式如下：

其中，表示以为底数的自然对数。代表模型输出，代表各个标签。中只有正确解的标签为1，其余均为0（one-hot表示）。

因此，交叉熵只计算对应着“正确解”标签的输出的自然对数。比如，假设正确标签的索引是“2”，与之对应的神经网络的输出是0.6，则交叉熵误差是；若“2”对应的输出是0.1，则交叉熵误差为。由此可见，交叉熵误差的值是由正确标签所对应的输出结果决定的。

梯度计算

为了梯度计算更加简洁，引入因子，定义损失函数（使用均方误差）如下：

其中是网络对第个样本的预测值：

梯度的定义：

可以计算出对和的偏导数：

从导数的计算过程可以看出，因子被消掉了，这是因为二次函数求导的时候会产生因子，这也是我们将损失函数改写的原因。

下面我们考虑只有一个样本的情况下，计算梯度：

可以计算出：

可以计算出对和偏导数：

梯度下降法

在现实中存在大量的函数正向求解容易，反向求解较难，被称为单向函数。这种函数在密码学中有大量的应用，密码锁的特点是可以迅速判断一个密钥是否是正确的(已知𝑥，求𝑦很容易)，但是即使获取到密码锁系统，无法破解出正确的密钥是什么（已知𝑦，求𝑥很难）。

这种情况特别类似于一位想从山峰走到坡谷的盲人，他看不见坡谷在哪（无法逆向求解出𝐿𝑜𝑠𝑠导数为0时的参数值），但可以伸脚探索身边的坡度（当前点的导数值，也称为梯度）。那么，求解Loss函数最小值可以这样实现：从当前的参数取值，一步步的按照下坡的方向下降，直到走到最低点。这种方法笔者称它为“盲人下坡法”。哦不，有个更正式的说法“梯度下降法”。

训练的关键是找到一组(𝑤,𝑏)，使得损失函数𝐿取极小值。

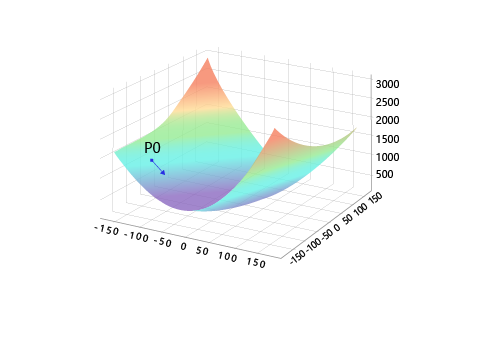
举个例子，假设有一个模型的损失函数如下图所示：

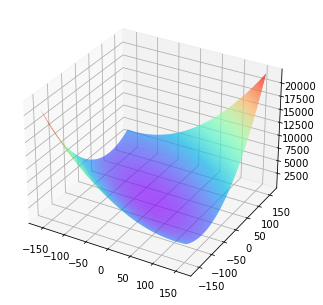
对于这种简单情形，我们可以利用程序，在三维空间中画出损失函数随参数变化的曲面图。从图中可以看出有些区域的函数值明显比周围的点小。

观察上述曲线呈现出“圆滑”的坡度，这正是我们选择以均方误差作为损失函数的原因之一。下图呈现了只有一个参数维度时，均方误差和绝对值误差（只将每个样本的误差累加，不做平方处理）的损失函数曲线图。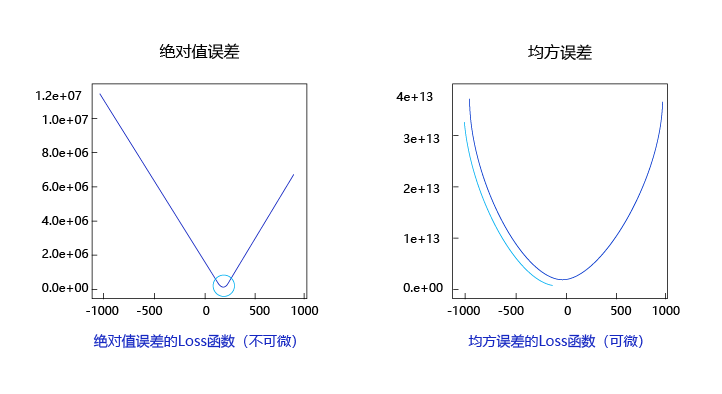

均方误差和绝对值误差损失函数曲线图

由此可见，均方误差表现的“圆滑”的坡度有两个好处：

• 曲线的最低点是可导的。
• 越接近最低点，曲线的坡度逐渐放缓，有助于通过当前的梯度来判断接近最低点的程度（是否逐渐减少步长，以免错过最低点）。

而这两个特性绝对值误差是不具备的，这也是损失函数的设计不仅仅要考虑“合理性”，还要追求“易解性”的原因。

现在我们要找出一组的值，使得损失函数最小，实现梯度下降法的方案如下：

• 步骤1：随机的选一组初始值，例如：
• 步骤2：选取下一个点，使得
• 步骤3：重复步骤2，直到损失函数几乎不再下降。

如何选择是至关重要的，第一要保证𝐿L是下降的，第二要使得下降的趋势尽可能的快。微积分的基础知识告诉我们，沿着梯度的反方向，是函数值下降最快的方向，如下图所示。简单理解，函数在某一个点的梯度方向是曲线斜率最大的方向，但梯度方向是向上的，所以下降最快的是梯度的反方向。

随机梯度下降法

在实际问题中，数据集往往非常大，如果每次都使用全量数据进行计算，效率非常低。由于参数每次只沿着梯度反方向更新一点点，因此方向并不需要那么精确。一个合理的解决方案是每次从总的数据集中随机抽取出小部分数据来代表整体，基于这部分数据计算梯度和损失来更新参数，这种方法被称作随机梯度下降法（Stochastic Gradient Descent，SGD），核心概念如下：

• mini-batch：每次迭代时抽取出来的一批数据被称为一个mini-batch。
• batch_size：一个mini-batch所包含的样本数目称为batch_size。
• epoch：当程序迭代的时候，按mini-batch逐渐抽取出样本，当把整个数据集都遍历到了的时候，则完成了一轮训练，也叫一个epoch。启动训练时，可以将训练的轮数num_epochs和batch_size作为参数传入。

训练配置

优化器

经过研究员的不断的实验，当前已经形成了四种比较成熟的优化算法：SGD、Momentum、AdaGrad和Adam，效果如下图所示。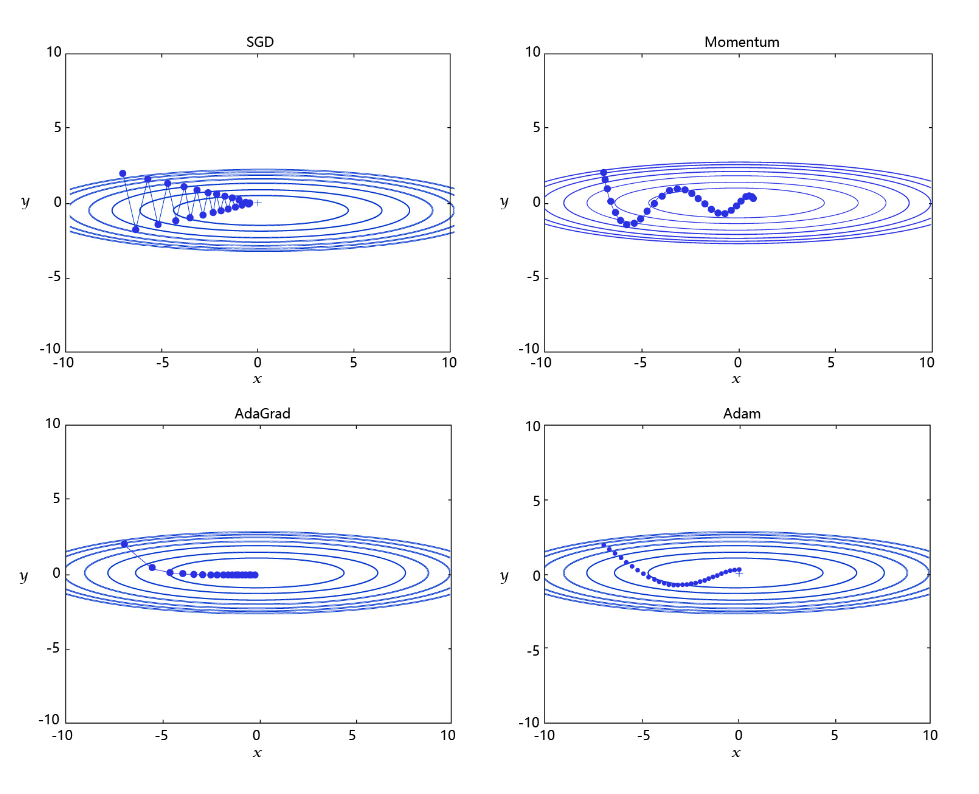

• SGD： 随机梯度下降算法，每次训练少量数据，抽样偏差导致的参数收敛过程中震荡。
• Momentum： 引入物理“动量”的概念，累积速度，减少震荡，使参数更新的方向更稳定。
• AdaGrad： 根据不同参数距离最优解的远近，动态调整学习率。学习率逐渐下降，依据各参数变化大小调整学习率。
• Adam： 由于动量和自适应学习率两个优化思路是正交的，因此可以将两个思路结合起来，这就是当前广泛应用的算法。

学习率

在深度学习神经网络模型中，通常使用标准的随机梯度下降算法更新参数，学习率代表参数更新幅度的大小，即步长。当学习率最优时，模型的有效容量最大，最终能达到的效果最好。学习率和深度学习任务类型有关，合适的学习率往往需要大量的实验和调参经验。探索学习率最优值时需要注意如下两点：

• 学习率不是越小越好。学习率越小，损失函数的变化速度越慢，意味着我们需要花费更长的时间进行收敛，如下图左图所示。
• 学习率不是越大越好。只根据总样本集中的一个批次计算梯度，抽样误差会导致计算出的梯度不是全局最优的方向，且存在波动。在接近最优解时，过大的学习率会导致参数在最优解附近震荡，损失难以收敛，如下图右图所示。

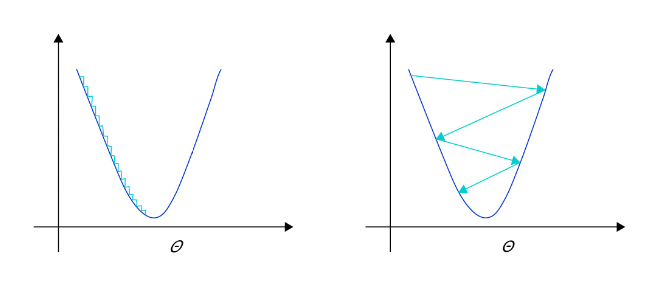
不同学习率（步长过大/过小）的示意图