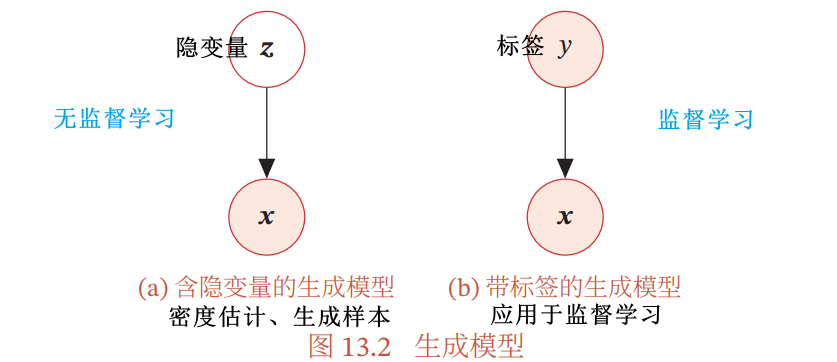
概率生成模型 / 生成模型：指一系列用于随机生成可观测数据的模型

• 生成模型是根据一些可观测的样本 （随机向量 服从一个未知的数据分布 ）学习一个参数化的模型 来近似未知分布 ，并可以用这个模型 生成一些样本，使得“生成”的样本和“真实的”样本尽可能地相似
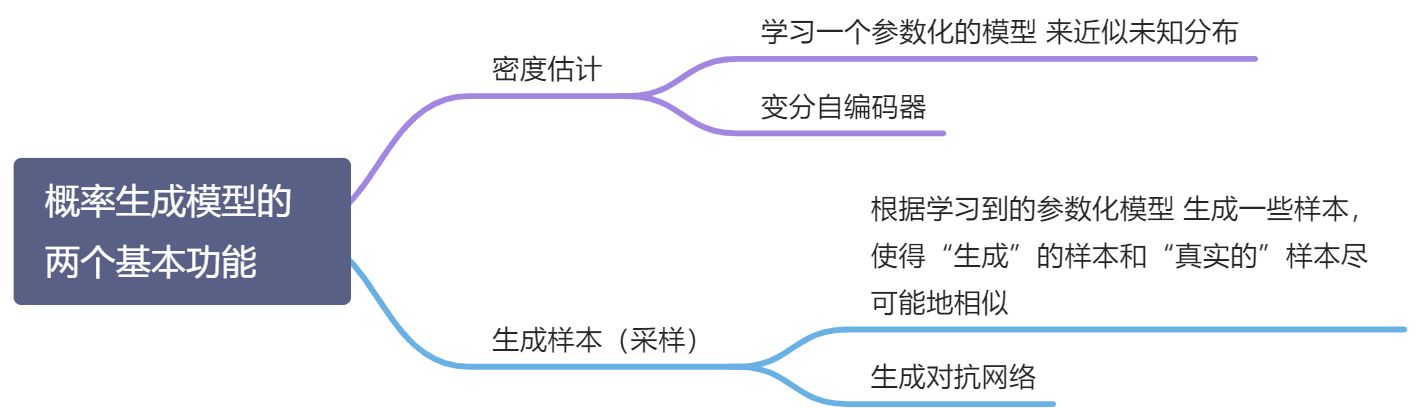
• 即，生成模型通常包含两个基本功能：
  • 概率密度估计：学习一个参数化的模型 来近似未知分布
  • 生成样本（采样）：根据学习到的参数化模型 生成一些样本，使得“生成”的样本和“真实的”样本尽可能地相似

• 深度生成模型：利用深度神经网络可以近似任意函数的能力来

  • 建模一个复杂分布 （即，概率密度估计）
  • or 直接生成符合分布 的样本（即，生成样本/采样）

    13.1 概率生成模型

    

    13.1.1 密度估计

    密度估计：根据数据集 D（数据独立地从相同的未知分布 中产生）来估计其概率密度函数

• 在机器学习中，密度估计是一类无监督学习问题

• 直接建模 比较困难，因此，通常引入隐变量 z 来简化模型，这样概率密度估计问题可以转换为估计变量 的两个局部条件概率 和
  • 为了简化模型，假设隐变量 z 的先验分布 为标准高斯分布 ，隐变量的每一维之间都是独立的，则先验分布 中没有参数，因此密度估计的重点是估计条件分布

变分自编码器：如果要建模含隐变量的分布，就需要利用 EM 算法来进行密度估计，需要估计条件分布 和近似后验分布 ，当这两个分布比较复杂时，利用神经网络来建模，就是变分自编码器的思想

13.1.2 生成样本 / 采样

生成样本 / 采样：给定一个概率密度函数为 的分布，生成一些服从这个分布的样本

采样过程：
得到两个变量的局部条件概率 后，就可以生成数据 x：

• 根据隐变量的先验分布 进行采样，得到样本 z
• 根据条件分布 进行采样，得到样本 x

为了便于采样， 通常不能太过复杂

生成对抗网络：从一个简单分布 （eg. 标准正态分布）中采集一个样本 z，并利用一个深度神经网络 使得 服从 ，就可以避免密度估计问题，直接生成样本，且能有效降低生成样本的难度，这就是生成对抗网络的思想

13.1.3 应用于监督学习

两类监督学习:

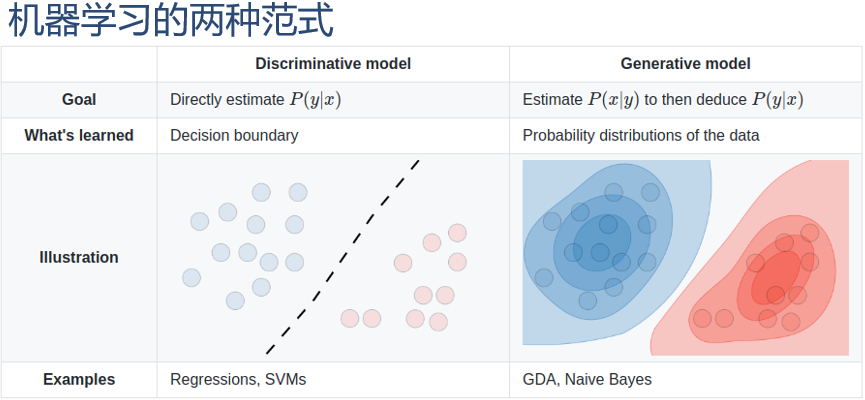
• 生成模型 Generative model：生成既可以用于生成样本，也可以用于监督学习
  • 监督学习的目标是建模样本 x 和输出标签 y 之间的条件概率分布
  • 根据贝叶斯公式 可以将监督学习问题转换为联合概率分布 的密度估计问题

• 例：朴素贝叶斯分类器、隐马尔可夫模型等
  • 判别模型 Discriminative model：判别模型直接建模条件概率分布 ,并不建模其联合概率分布
• 例：Logistic 回归、支持向量机、神经网络等

13.2 变分自编码器 VAE

13.2.1 含隐变量的生成模型

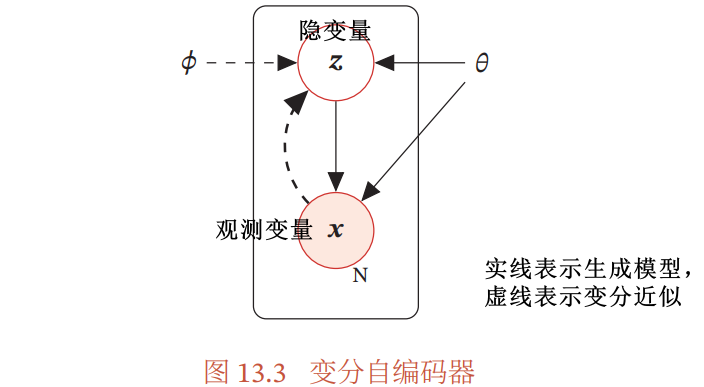
如上图所示的含隐变量的生成模型：

• 联合概率密度可以分解为

• 一般情况下，可以假设 隐变量 z 的先验分布的密度函数 和已知 z 时观测变量 x 的条件概率密度函数 为某种参数化的分布族（eg. 正态分布），可以通过最大化似然来进行估计
• 样本 x 的对数边际似然可以分解为
  • 变分密度函数
  • 证据下界
  • 最大化对数边际似然 可以用 EM 算法求解
    • E 步：固定 θ，寻找一个密度函数
      • 后验概率 很难计算，通常用变分推断来近似估计，即用简单的分布 来近似推断 。但当 比较复杂时，近似效果不佳
    • M 步：固定 ，寻找 θ 来最大化

变分自编码器 VAE：利用神经网络来分别建模两个复杂的条件概率密度函数

• 推断网络：用神经网络来估计变分分布 ，一般写为
  • 因为 的目标是近似后验分布
  • 输入 x，输出变分分布
• 生成网络：用神经网络来估计概率分布
  • 输入 z，输出概率分布

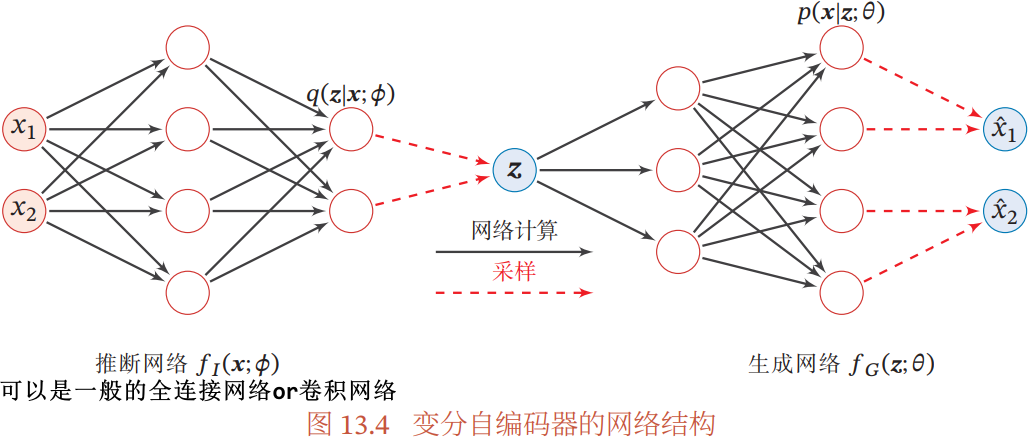
13.2.2 推断网络

推断网络 ，输入 x，输出变分分布

• 假设变分分布 ，即服从对角化协方差的高斯分布
  • 高斯分布的均值 和方差 可以通过推断网络 预测，即

推断网络的目标：使得 尽可能接近真实的后验

• 需要找到一组网络参数 来最小化这两个分布的 KL 散度：
• 可转化为：，即寻找一组网络参数 使得证据下界 最大

13.2.3 生成网络

生成网络 ，输入 z，输出概率分布

• 隐变量 z 的先验分布 ：一般假设为各向同性的标准高斯分布
  • 隐变量的每一维之间都是独立的

• 条件概率分布 ：通过生成网络来建模

  • 假设条件概率分布 可以用参数化的分布族表示，分布族的参数可以通过生成网络计算得到
    • 若 x 是 D 维的二值向量，可以假设 服从多变量的伯努利分布
    • 若 x 是 D 维的连续向量，可以假设 服从对角化的协方差的高斯分布

• 生成网络的目标：，即寻找一组网络参数 来最大化证据下界

13.2.4 模型汇总

上面得到，推断网络和生成网络的目标都是最大化证据下界
→
变分自编码器的总目标函数：

• 变分自编码器优化推断网络和生成网络的过程，可以分别看作 EM 算法的 E 步和 M 步
• 但在变分自编码器中，这两步的目标合二为一，都是最大化证据下界

13.2.5 再参数化

再参数化：将一个函数 的参数 用另外一组参数表示 ，函数 转化为参数为 的函数

上面得到的变分自编码器的总目标函数中的期望 ，通过再参数化将 z 和 Φ 之间随机性的采样关系转变为确定性函数关系

再参数化是实现通过随机变量实现反向传播的一种重要手段

13.2.6 训练

通过再参数化，变分自编码器可以通过梯度下降法来学习参数，从而提高变分自编码器的训练效率

• 模型汇总一节中得到，变分自编码器的目标函数近似为：
• 如果采用随机梯度法，每次从数据集中采集一个样本 x 和一个对应的随机变量 ，并进一步假设 服从高斯分布 ，则目标函数简化为：

变分自编码器的训练过程：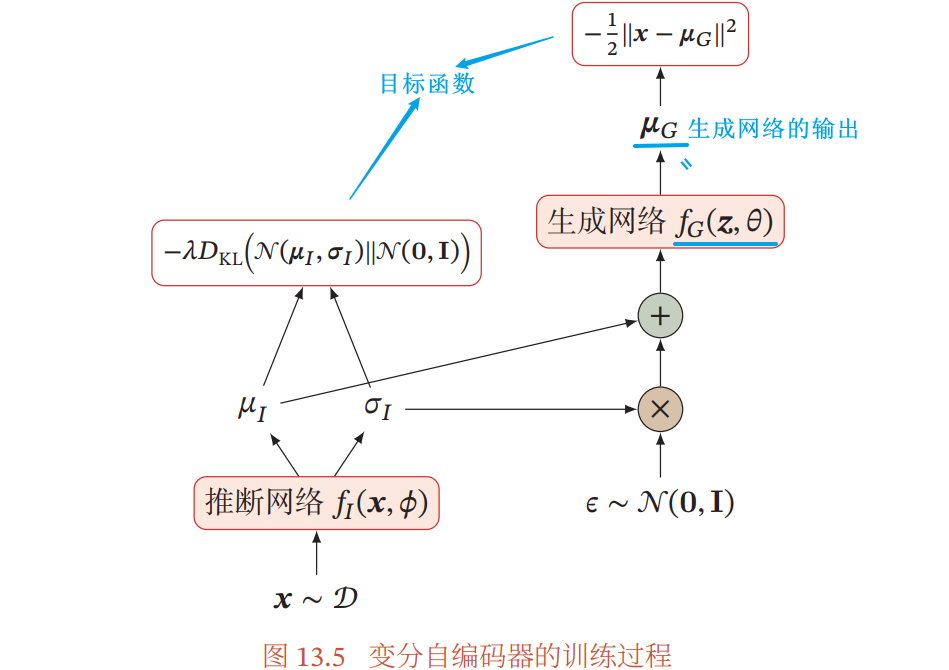

变分自编码器学习到的隐变量流行：

13.3 生成对抗网络 GAN

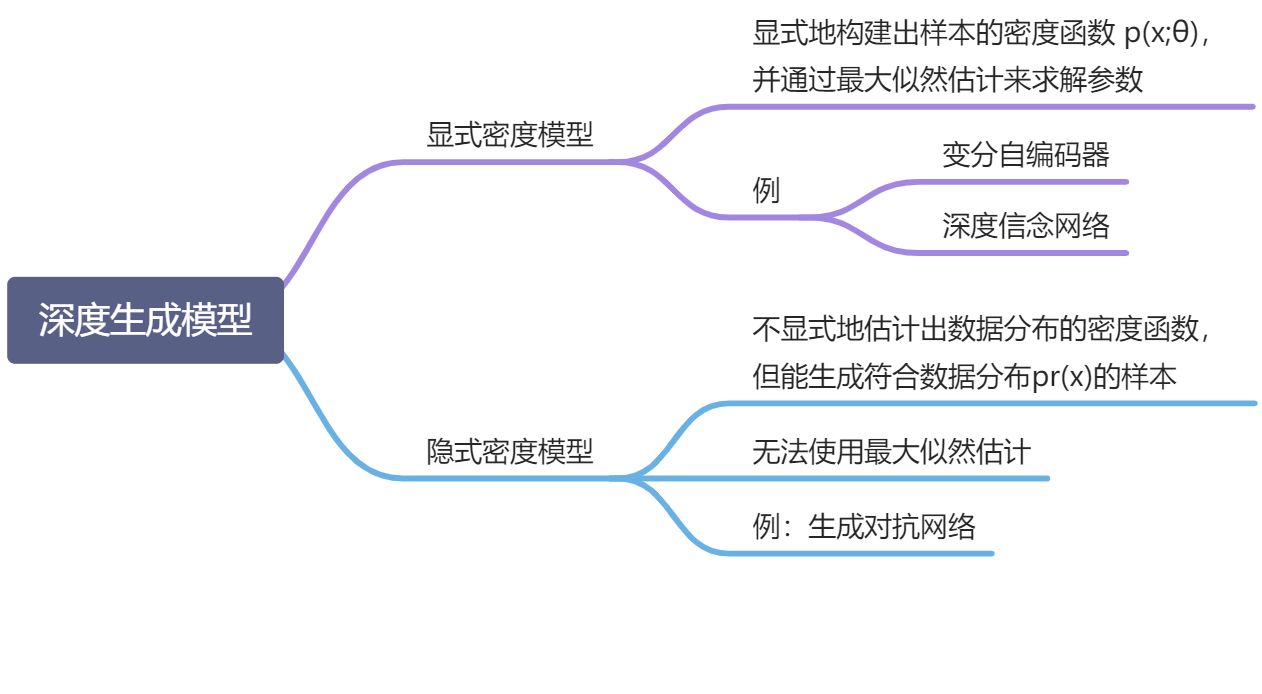
13.3.1 显示密度模型和隐式密度模型

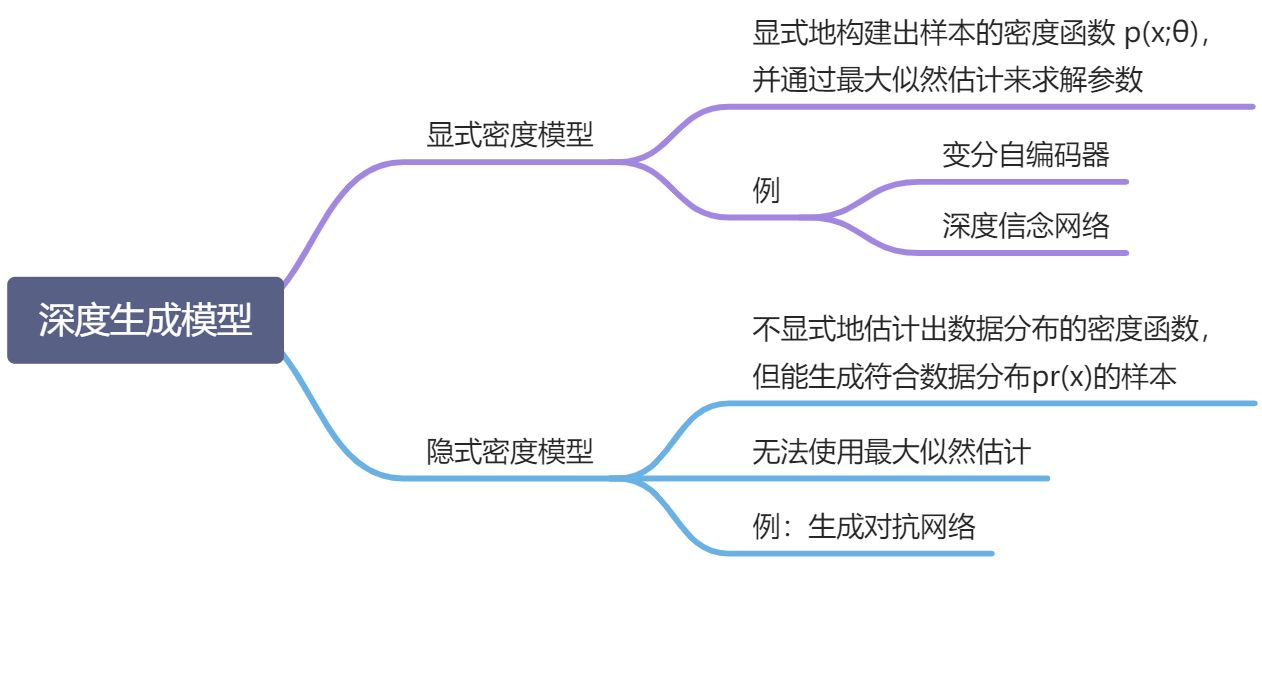隐式密度模型：不显式地建模真实分布 ，而是建模生成过程

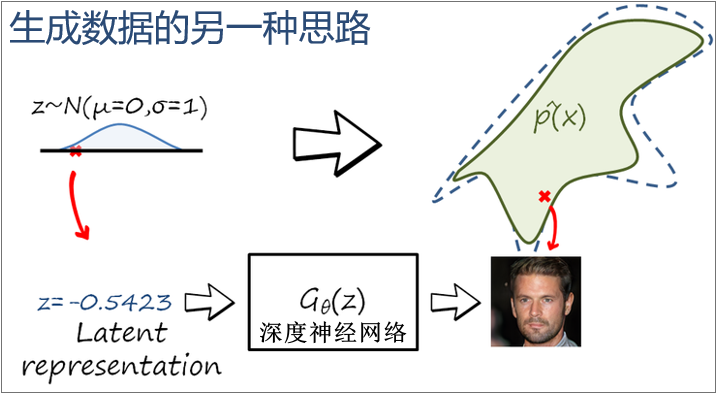
• 生成网络：从隐空间（latent space）中随机采样作为输入，其输出结果需要尽量模仿训练集中的真实样本

13.3.2 网络分解

隐式密度模型的关键：如何确保生成网络产生的样本一定是服从真实的数据分布

生成对抗网络 GAN（Generative Adversarial Networks）：通过对抗训练的方式使得生成网络产生的样本服从真实的数据分布

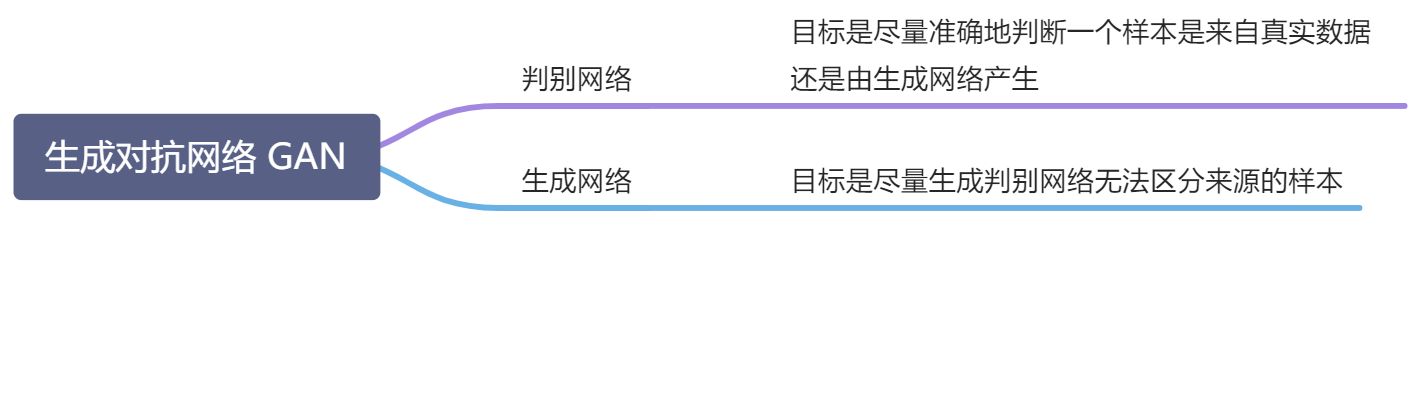
• 目标相反的判别网络和生成网络不断交替训练，最后收敛时，如果判断网络再也无法判断出一个样本的来源，就相当于生成网络可以生成符合真是数据分布的样本

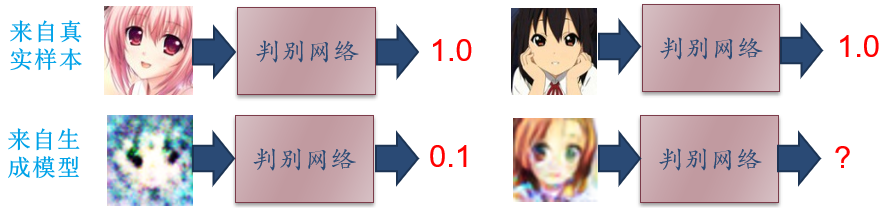
13.3.2.1 判别网络

判别网络 ：目标是区分出一个样本 x 是来自于真实分布 还是来自于生成模型

• 是一个二分类的分类器
• 输入 x 为真实样本或生成网络的输出
• 输出为 x 属于真是数据分布的概率
• 目标函数为最小化交叉熵

13.3.2.2 生成网络

生成网络 ：目标是让判别网络将自己生成的样本判别为真实样本

• 目标函数

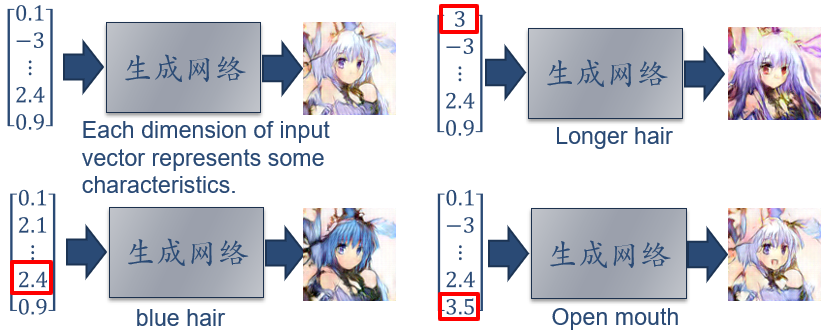
13.3.3 训练

对抗训练：

• 生成网络要尽可能地欺骗判别网络
• 判别网络将生成网络生成的样本与真实样本尽可能区分出来

两个网络相互对抗、不断调整参数，最终目的是使判别网络无法判断生成网络的输出结果是否真实

生成对抗网络的目标函数可以看作最小化最大化游戏：

• 判别网络的目标函数：
• 生成网络的目标函数：
• 生成对抗网络的整体目标函数：

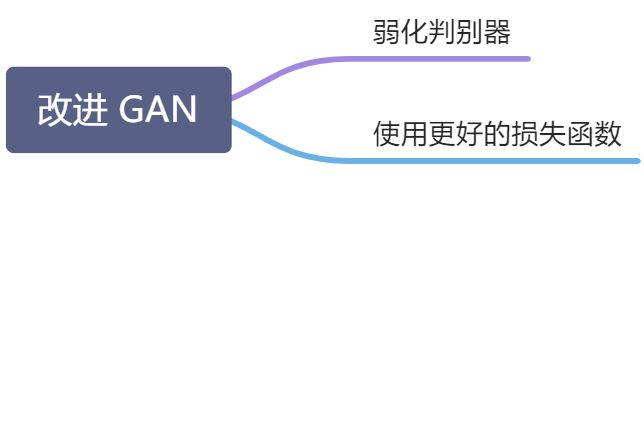
训练技巧：使得在每次迭代时，判别网络比生成网络的能力强一些，但又不能强太多

13.3.4 DCGAN：一个生成对抗网络的具体实现

深度卷积生成对抗网络 DCGAN：

• 判别网络是一个传统的深度卷积网络，但是用了带步长的卷积来实现下采样操作，不用最大汇聚/池化操作
• 生成网络使用一个特殊的深度卷积网络实现：使用微步卷积来生成 64×64 的图像
  • 第一层是全连接层，然后是四层的微步卷积，没有汇聚层/池化层

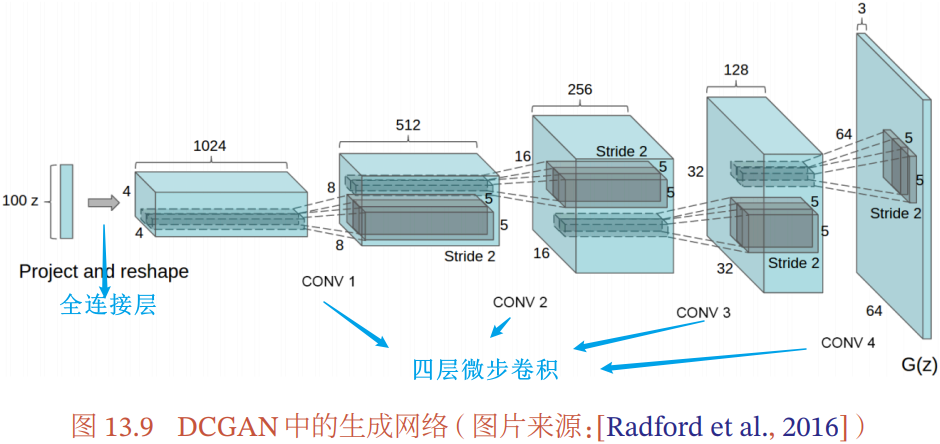
DCGAN 的主要优点：通过一些经验性的网络结构设计使得对抗训练更加稳定

• 判别网络中使用带步长的卷积、生成网络中使用微步卷积，代替汇聚/ 池化操作，以免信息损失
• 使用批量归一化
• 去除卷积层之后的全连接层
• 在生成网络中，除了最后一层使用 Tanh 激活函数外，其余层都用 ReLU 函数
• 在判别网络中，都使用 LeakyReLU 激活函数

13.3.5 模型分析

• 最优判别器
• 生成对抗网络的目标函数：

  13.3.5.1 训练稳定性

  在生成对抗网络中，当判别网络为最优时，生成网络的优化目标是最小化真实分布 和模型分布 之间的 JS 散度。当两个分布相同时，JS 散度为 0，最优生成网络 对应的损失为

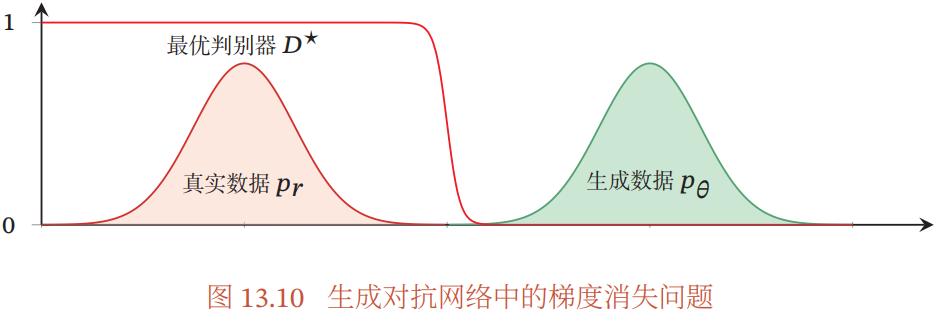
不稳定性：生成网络的梯度消失问题

• 使用 JS 散度来训练生成对抗网络，当两个分布没有重叠时，它们之间的 JS 散度恒等于常数 log 2。对生成网络来说，目标函数关于参数的梯度为 0
• 解决：一般不将判别网络训练到最优，只进行一步或多步梯度下降，使得生成网络的梯度依然存在
  • 但判别网络也不能太差，否则生成网络的梯度为错误的梯度
  • 但是很难在梯度消失和梯度错误之间取得平衡，使得生成对抗网络在训练时稳定性较差

13.3.5.2 模型坍塌

• 生成网络的目标函数
  • 后两项与生成网络无关
• ∴
  • JS 散度 为有界函数，因此生成网络的目标更多的是受 影响，使得生成网络更倾向于生成一些更“安全”的样本，从而造成模型坍塌问题

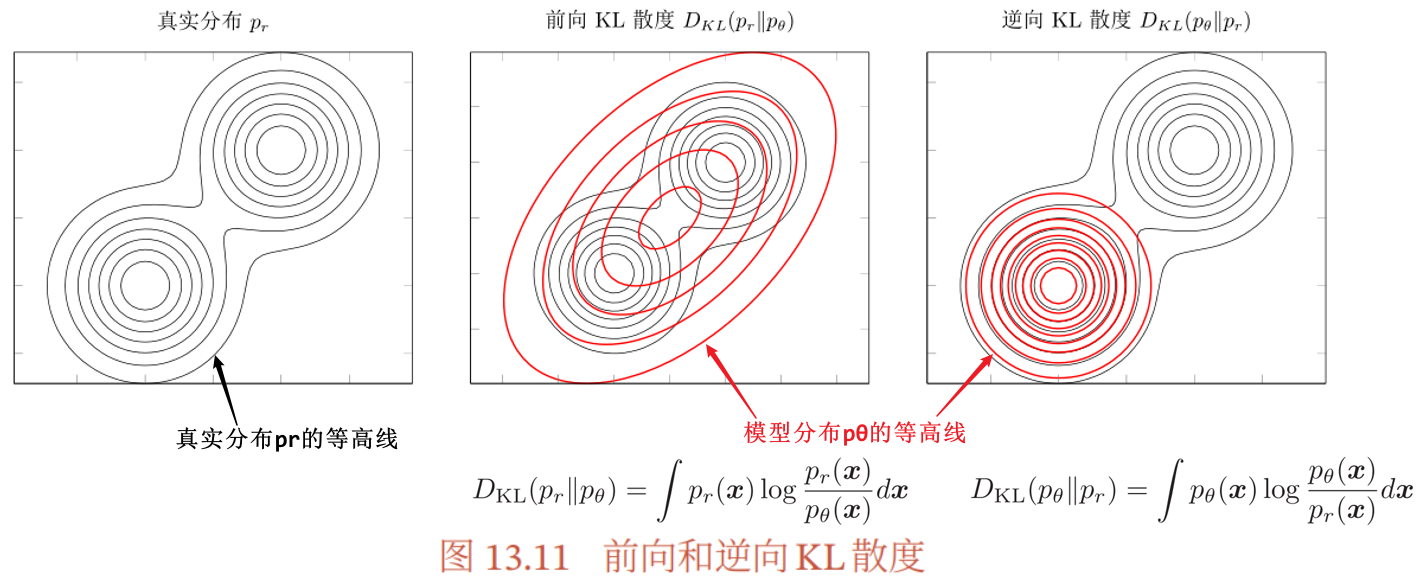
前向和逆向 KL 散度

• 前向 KL 散度
  • 鼓励模型分布 尽可能覆盖所有真实分布 的点，而不用回避 的点
• 逆向 KL 散度
  • 鼓励模型分布 尽可能避开所有真实分布 的点，而不需要考虑是否覆盖所有真实分布 的点

13.3.6 改进模型

上面提到，通过优化交叉熵（JS 散度）训练生成对抗网络会导致训练稳定性和模型坍塌问题，因此 JS 散度不适合衡量生成对抗网络的生成数据分布和真实数据分布的距离，需要使用其他损失函数

13.3.6.1 W-GAN

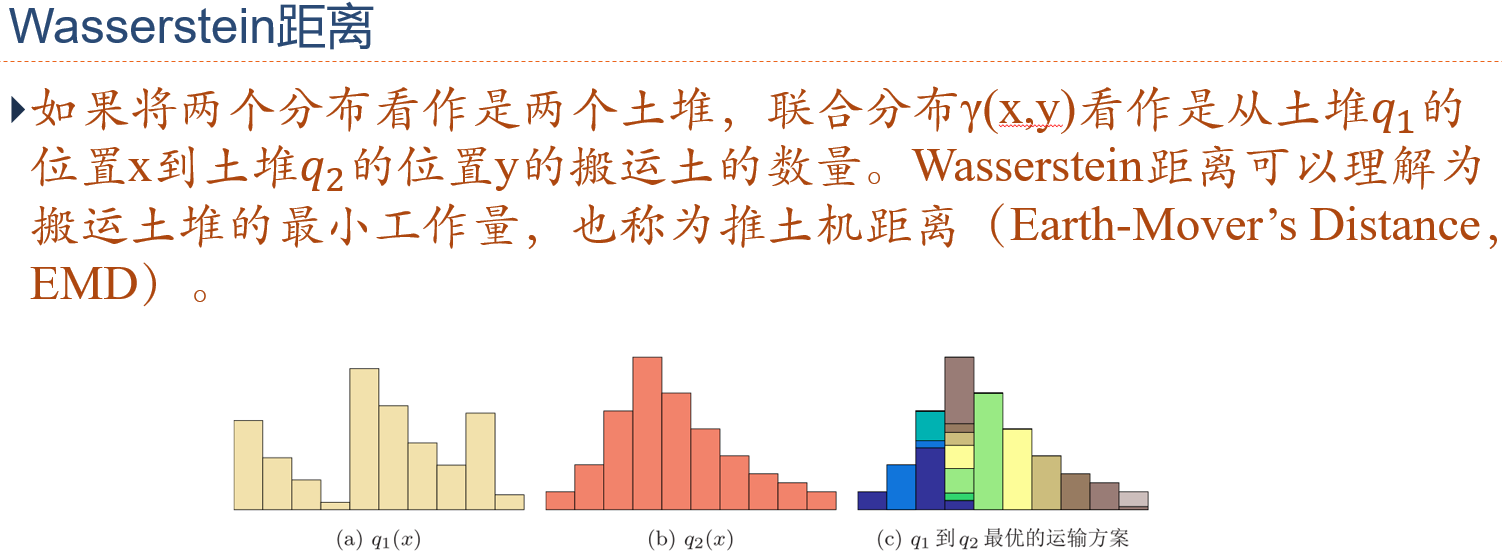
Wasserstein 距离 / 推土机距离：用于衡量两个分布之间的距离

• 
  • 是边际分布为 的所有可能的联合分布集合
  • 为 x 和 y 的距离
• Wasserstein 距离相比 KL 散度和 JS 散度的优势：即使两个分布没有重叠或重叠非常少，Wasserstein 距离仍然能反映出两个分布的远近

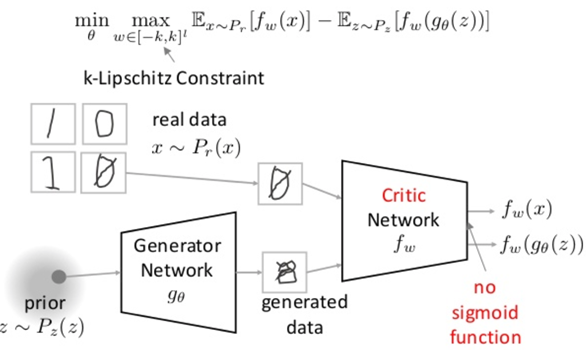
W-GAN：通过用 Wasserstein 距离（） 替代 JS 散度来优化训练的生成对抗网络

• 生成网络参数 θ 的梯度不会消失，理论上解决了原始 GAN 训练不稳定的问题
• 一定程度上缓解了模型坍塌问题，使得生成的样本具有多样性

训练过程：

13.4 总结和深入阅读

深度生成模型是一种有机融合神经网络和概率图模型的生成模型，将神经网络作为一个概率分布的逼近器，可以拟合非常复杂的数据分布

• 变分自编码器：利用神经网络的拟合能力，解决含隐变量的概率模型中后验分布难以估计的问题
  • 再参数化：是变分自编码器的重要技巧
• 生成对抗网络：
  • 训练不稳定问题的一种解决方案：W-GAN，用 Wasserstein 距离代替 JS 散度来进行训练

深度生成模型作为一种无监督模型，其主要缺点：

• 缺乏有效的客观评价，很难客观衡量不同模型之间的优劣

习题

习题 13-1 对于一个分布为𝑝𝜃(𝑧)的离散随机变量𝑧，以及函数 𝑓(𝑧)，如何计算期望 关于分布参数𝜃 的导数

习题 13-2 推导公式(13.28)

习题 13-3 通过分析公式(13.28)，给出变分自编码器和自编码器在内在机理上的不同之处

习题 13-4 假设一个二分类问题，类别为 ，并有 ．样本𝒙在两个类的条件分布为 ，一个分类器 用于预测一个样本𝒙来自类别 的条件概率．证明若采用交叉熵损失 ，则最有分类器

习题 13-5 分析下面函数是否满足Lipschitz连续条件

1. 
2. 
3. 
4. 

习题 13-6 证明公式(13.54)