 本章重点:
本章重点:
- 深度信念网络:一种可以有效学习变量之间复杂依赖关系的概率图模型
- 网络中包含很多层的隐变量,可以有效地学习数据的内部特征表示(这些学习到的内部特征表示包含了数据的更高级的、有价值的信息,有助于后续的分类和回归等任务),也可以作为一种有效的非线性降维方法
铺垫:两种相关的基础模型:
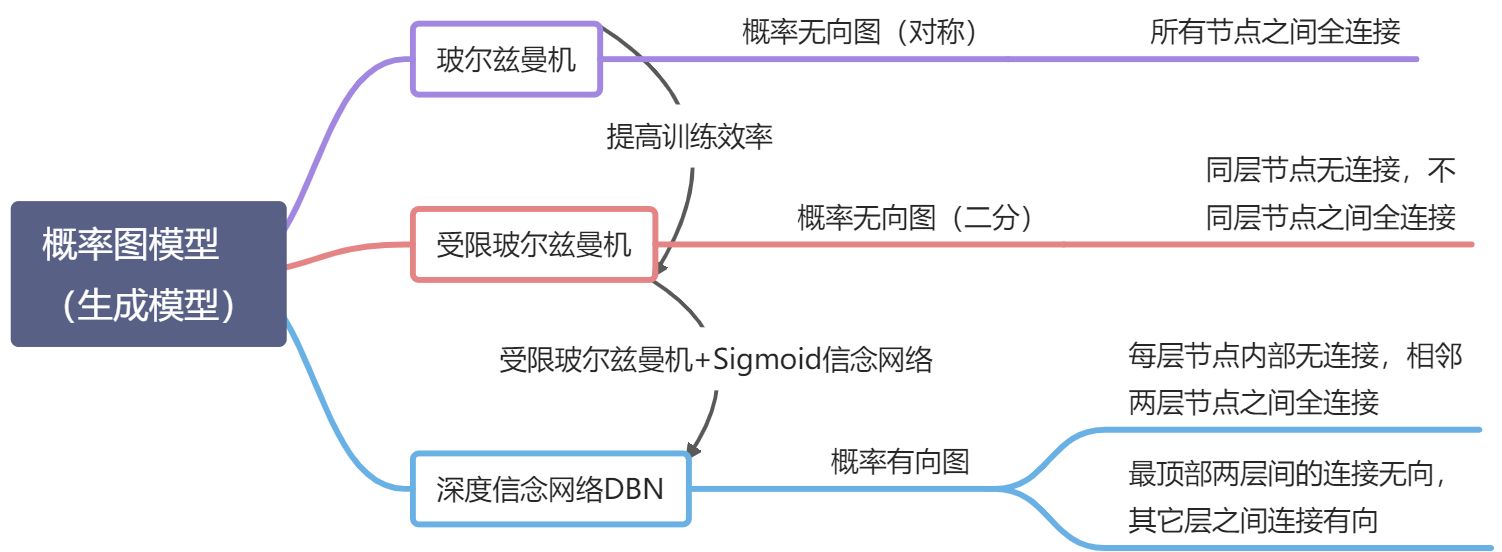
生成模型:玻尔兹曼机和深度信念网络都是生成模型,借助隐变量来描述复杂的数据分布
概率图模型:玻尔兹曼机和深度信念网络作为概率图模型的共同问题:推断和学习问题
- 两种模型都比较复杂,且包含隐变量,因此推断和学习一般通过 MCMC 方法来近似,生成一组服从
分布的样本
随机神经网络 SNN:玻尔兹曼机和深度信念网络和神经网络有很强的对应关系,在一定程度上也称为随机神经网络
12.1 玻尔兹曼机
玻尔兹曼分布:是描述一个粒子处于特定状态 α 下的概率
,是关于状态能量与系统温度的函数
为状态 α 的能量函数,k 为玻尔兹曼常量,T 为系统温度
为玻尔兹曼因子,是没有归一化的概率
为归一化因子,称为配分函数
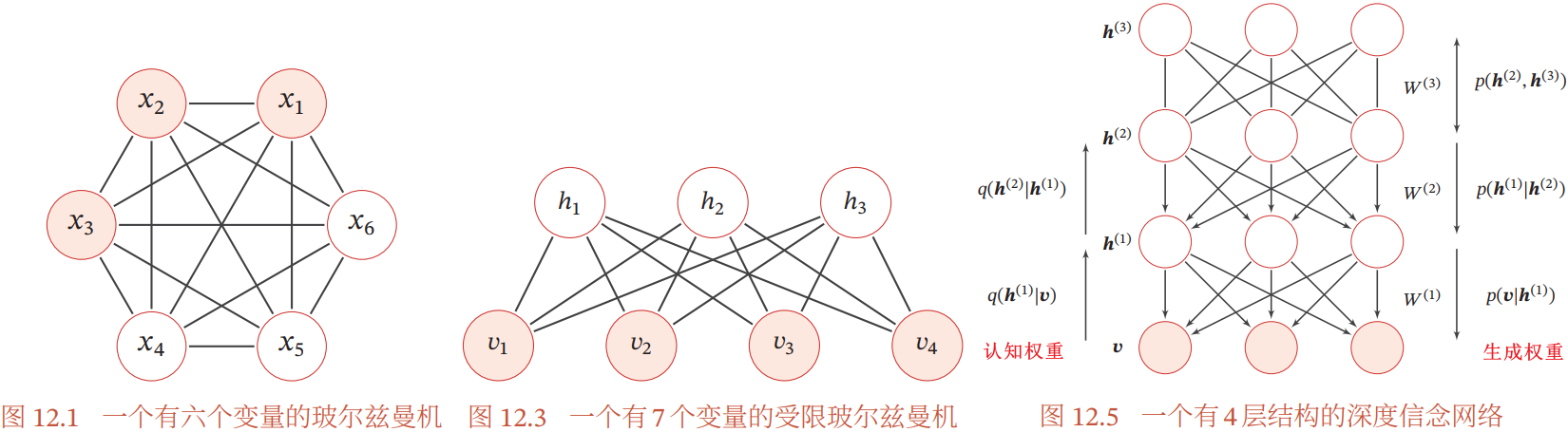
玻尔兹曼机:是一个随机动力系统,每个变量的状态都以一定的概率受到其他变量的影响
- 玻尔兹曼机可以用概率无向图模型描述
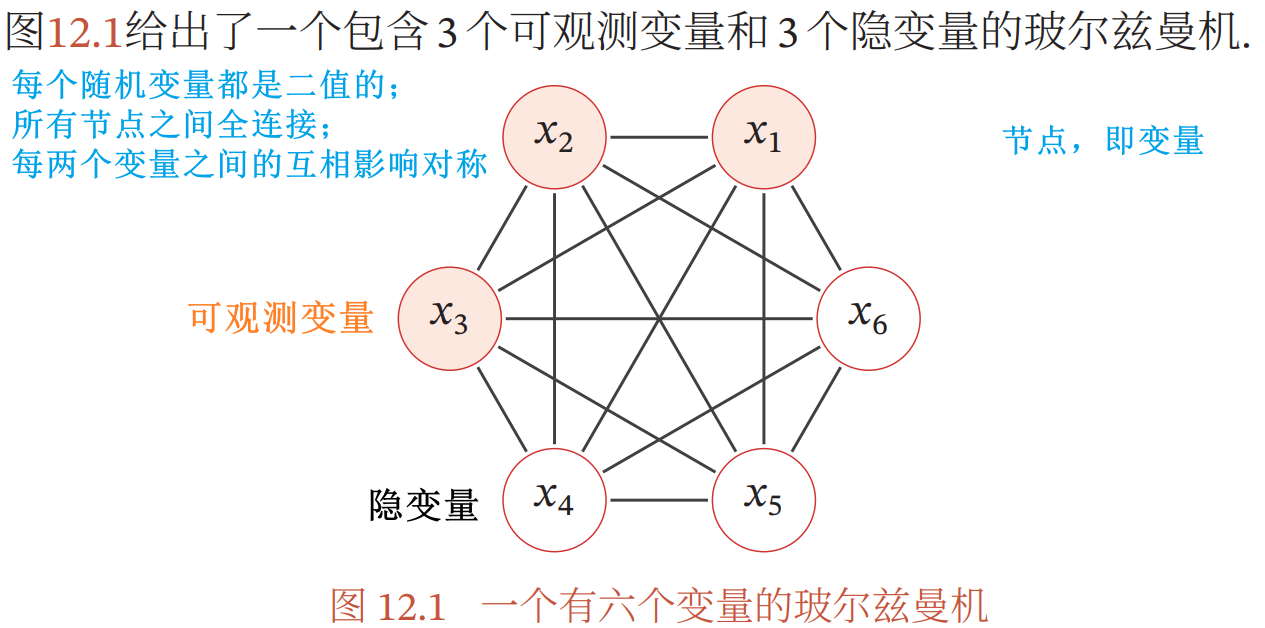
- 一个具有 K 个节点(变量)的玻尔兹曼机满足三个性质:
- 每个随机变量是二值的
- 二值的随机向量
:所有的随机变量
- 可观测变量 V
- 隐变量 H
- 二值的随机向量
- 所有节点之间是全连接的,每个变量
都依赖于所有其它变量
- 每两个变量之间的互相影响(
)是对称的
- 每个随机变量是二值的
- 随机向量 X 的联合概率
(由玻尔兹曼分布得到,将玻尔兹曼常数 k 吸收到温度 T 中了)
- 玻尔兹曼机中配分函数 Z 通常难以计算,因此联合概率一般通过 MCMC 方法来近似,生成一组服从
分布的样本
- 玻尔兹曼机中配分函数 Z 通常难以计算,因此联合概率一般通过 MCMC 方法来近似,生成一组服从
- 能量函数
是变量
之间的连接权重
是变量
的偏置
- 如果两个变量
的取值都为 1
- 一个正的权重
会使得玻尔兹曼机的能量下降,发生的概率变大
- 一个负的权重
会使得玻尔兹曼机的能量上升,发生的概率变小
- 一个正的权重
- 因此,如果令玻尔兹曼机中每个变量
代表一个基本假设,其取值 1 or 0 代表模型接受 or 拒绝该假设,那么变量之间连接的权重代表了两个假设之间的弱约束关系
- 连接权重为正表示两个假设可以相互支持,即一个假设若被接受,另一个也很可能被接受
- 连接权重为负表示两个假设不能同时被接受
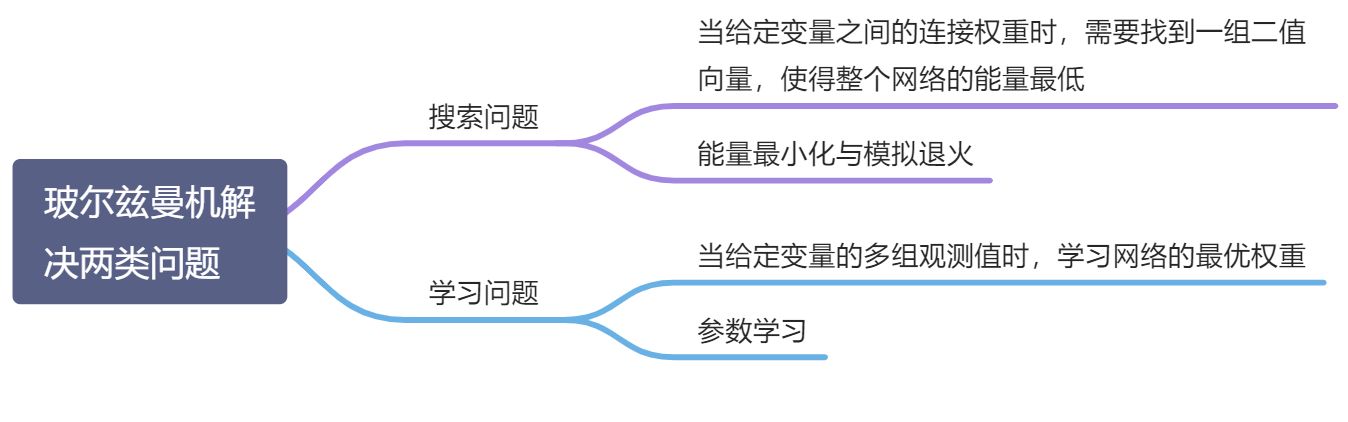
玻尔兹曼机可以用来解决两类问题:
- 搜索问题:当给定变量之间的连接权重时,需要找到一组二值向量,使得整个网络的能量最低
- 学习问题:当给定变量的多组观测值时,学习网络的最优权重
12.1.1 生成模型
上面提到,由于玻尔兹曼机中配分函数 Z 通常难以计算,因此联合概率一般通过 MCMC 方法来近似,生成一组服从分布的样本。本节介绍基于吉布斯采样的样本生成方法
玻尔兹曼机中变量的全条件概率:
- 保持其它变量
不变,变量
的状态从 0(关闭) 到 1 (打开)之间的能量差异
- 保持其它变量
玻尔兹曼机的吉布斯采样过程:
- 随机选择一个变量
- 根据其全条件概率
来设置其状态,即以
的概率将变量
设为 1,否则设为 0
- 在固定温度 T 的情况下,在运行足够时间后,玻尔兹曼机会达到热平衡
- 热平衡:此时,任何全局状态的概率服从玻尔兹曼分布
,只与系统的能量有关,与初始状态无关
- 玻尔兹曼机达到热平衡的收敛速度和温度 T 有关
- 当温度很高
时,
,可以很快达到热平衡
- 当温度很低
时,随机性方法变成了确定性方法,玻尔兹曼机退化为一个 Hopfield 网络
- 若
,则
- 若
,则
- 若
- 当温度很高
- 玻尔兹曼机达到热平衡的收敛速度和温度 T 有关
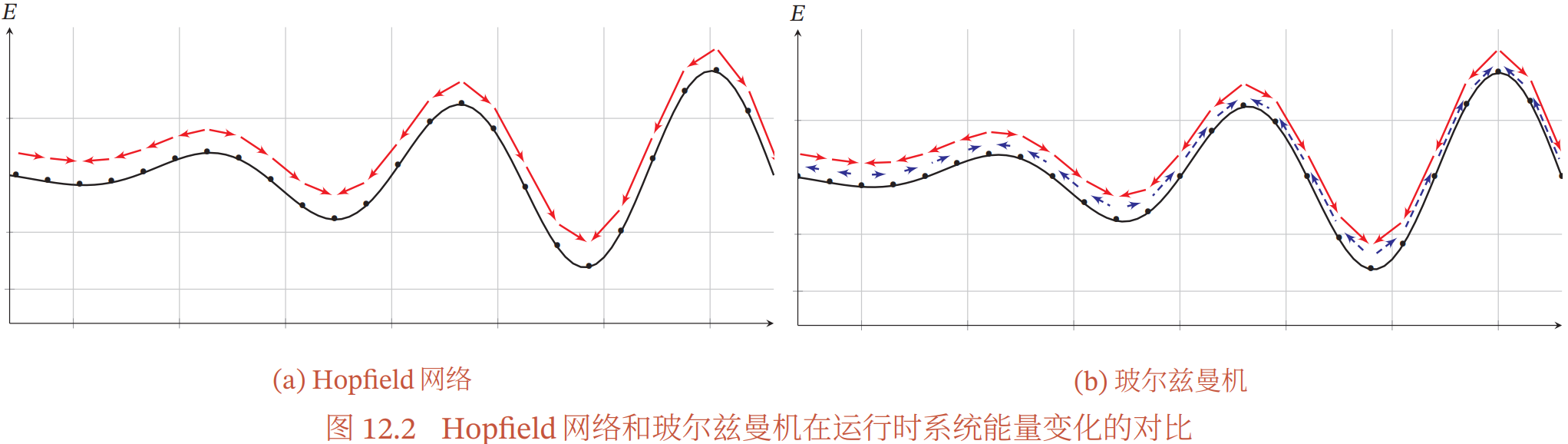
玻尔兹曼机和 Hopfield 网络的区别:
- Hopfield 网络是一种确定性的动力系统,每次状态更新都会是的系统的能量降低
- 玻尔兹曼机是一种随机性的动力系统,以一定的概率使得系统的能量上升
12.1.2 能量最小化与模拟退火
能量最小化:在一个动力系统中,找到一个状态使得能量最小,是一个重要的优化问题
- Hopfield 网络是收敛到局部最优点(吸引点),而不是全局最优,不过这对于 Hopfield 网络来说并不是缺点,相反是用局部最优点来存储信息
- 为了跳出局部最优解,就要允许偶尔可以将一个变量设置为使得能量变高的状态。需要引入一定的随机性,以
的概率将变量
设为 1,否则设为 0(和吉布斯采样过程类似)
模拟退火:是一种寻找全局最优的近似方法。让系统开始在一个比较高的温度下运行达到热平衡,然后逐渐降低,直到系统在一个比较低的温度下运行达到热平衡,就得到一个能量全局最小的分布
12.1.3 参数学习
参数学习:给定一组可观测的向量 作为训练集,要学习玻尔兹曼机的参数 W 和 b 使得训练集中所有样本的对数似然函数最大
假设一个玻尔兹曼机有 K 个变量,包括 个可观测变量
和
个 隐变量
- 训练集 D 的对数似然函数:
- 对数似然函数对权重参数
和偏置参数
的偏导数:
- 这两个公式都涉及计算配分函数和期望,很难精确计算且耗时,因此一般通过 MCMC 方法(eg. 吉布斯采样)来近似求解
12.2 受限玻尔兹曼机 RBM
玻尔兹曼机的缺点:由于其复杂性,并未得到广泛使用。虽然基于采样的方法在很大程度上提高了学习效率,但是每更新一次权重,就需要网络更新达到热平衡状态,这个过程依然比较低效,需要很长时间
- 因此实际中,广泛使用的是受限玻尔兹曼机
受限玻尔兹曼机 RBM:是一个二分图结构的无向图模型
- 分为可观测层和隐藏层两组变量
- 同层节点之间无连接,不同层节点之间全连接(类似于两层全连接神经网络)
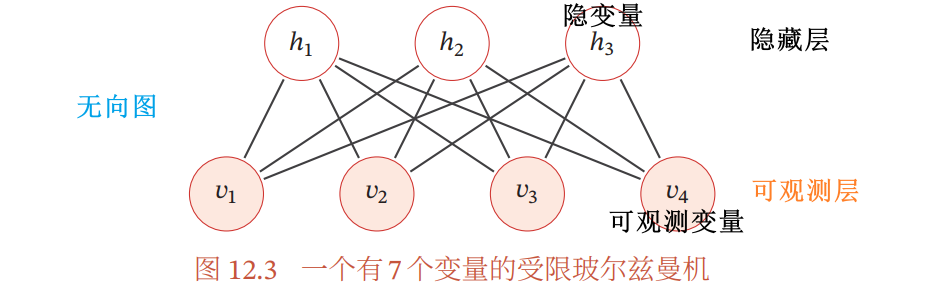
受限玻尔兹曼机的组成: 个可观测变量和
个隐变量
- 可观测的随机向量
- 隐藏的随机向量
- 权重矩阵
:每个元素
为可观测变量
和隐变量
之间边的权重
- 可观测随机向量的偏置矩阵
和隐藏随机向量的偏置矩阵
受限玻尔兹曼机的能量函数:
受限玻尔兹曼机的联合概率分布
- 配分函数
12.2.1 生成模型
在给定受限玻尔兹曼机的联合概率分布 后,可以通过吉布斯采样方法生成一组服从
的样本
全条件概率:
(由无向图性质,给定隐变量时,可观测变量之间相互独立)
(由无向图性质,给定可观测变量时,隐变量之间相互独立)
受限玻尔兹曼机中变量的条件概率:
条件概率的向量形式:
吉布斯采样:在受限玻尔兹曼机的全条件概率中,可观测变量之间互相条件独立,因变量之间也互相条件独立,因此受限玻尔兹曼机可以并行地对所有的可观测变量(or 所有的隐变量)同时进行采样,从而更快地达到热平衡状态
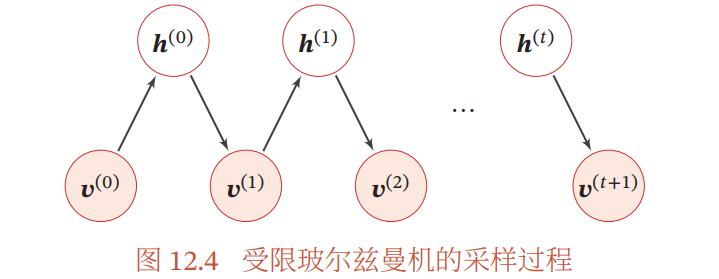
受限玻尔兹曼机的采样过程:
- 给定 or 随机初始化一个可观测的向量
,计算隐变量的概率,并从中采样一个隐向量
- 基于
,计算可观测变量的概率,并从中采样一个可观测的向量
- 重复 t 次后,得到
,当 t→∞时,
采样服从
分布
12.2.2 参数学习
参考 玻尔兹曼机的参数学习,也是通过最大化似然函数来找到最优的参数
训练集 的对数似然函数
对数似然函数对参数的偏导数:
,
为训练集上 v 的实际分布
以上公式需要计算配分函数 Z 以及两个期望,很难计算,一般通过 MCMC 方法近似
- 首先将可观测向量 v 设为训练样本中的值并固定,根据条件概率对隐向量 h 进行采样,此时受限玻尔兹曼机的值记为
- 然后不固定可观测向量 v,通过吉布斯采样轮流更新 v 和 h
- 当达到热平衡状态时,采集 v 和 h 的值,记为
采用梯度上升法,近似地更新参数:
使用吉布斯采样时,受限玻尔兹曼机的采样效率比一般的玻尔兹曼机有很大提高,但一般还是需要很多步采样才可以采集到符合真实分布的样本
12.2.2.1 对比散度学习算法 CD-k
对比散度学习算法:适用于受限玻尔兹曼机的一种比吉布斯采样更有效的参数学习算法,仅需 k 步(k=1 就可以学得很好)吉布斯采样
- 用一个训练样本作为可观测向量的初始值
- 然后,交替对可观测向量和隐向量进行吉布斯采样,不需要等到收敛,只需要 k 步就足够了,通常 k=1 就能学得很好

12.2.3 受限玻尔兹曼机的类型
| 受限玻尔兹曼机的类型 | 描述 |
|---|---|
| “伯努利-伯努利”受限玻尔兹曼机 | 可观测变量和隐变量都为二值类型 |
| “高斯-伯努利”受限玻尔兹曼机 | 可观测变量为高斯分布(连续值),隐变量为伯努利分布(二值) |
| “伯努利-高斯”受限玻尔兹曼机 | 可观测变量为伯努利分布(二值),隐变量为高斯分布(连续值) |
12.3 深度信念网络 DBN
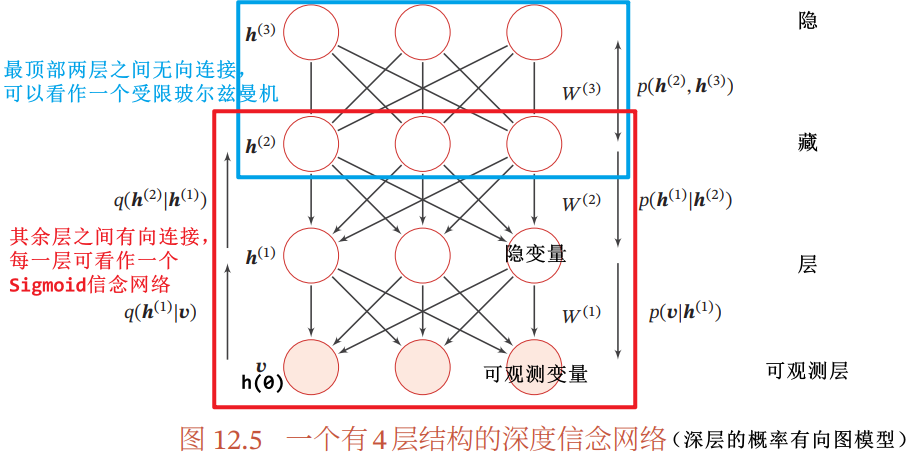
深度信念网络 DBN:一种深层的概率有向图模型
- 每层节点内部无连接,相邻两层节点之间为全连接
- 网络的最底层为可观测变量,其它层节点都为隐变量
- 最顶部的两层间的连接无向(顶部两层可以看作一个受限玻尔兹曼机),其余层之间的连接有向(每一层都可以看作一个 Sigmoid 信念网络)
- 对于含有 L 层隐变量的深度新网络,顶部两层可以看作一个受限玻尔兹曼机(无向图模型),用来产生
的先验分布
- 除了最顶上两层外,其余层每一层都可以看作一个 Sigmoid 信念网络(有向图模型),每一层变量
依赖上一层
,
为 Sigmoid 型条件概率
- 对于含有 L 层隐变量的深度新网络,顶部两层可以看作一个受限玻尔兹曼机(无向图模型),用来产生
12.3.1 生成模型
- 深度信念网络是一个生成模型,可以用来生成符合特定分布的样本
- 隐变量用来描述可观测变量之间的高阶相关性
生成样本的过程:
- 首先运行最顶层的受限玻尔兹曼机进行足够多次的吉布斯采样,在达到热平衡时生成样本
- 然后依次计算下一层变量的条件分布
并采样
- 自顶向下逐层采样,最终得到可观测层的样本
12.3.2 参数学习
深度信念网络最直接的训练方式是最大化可观测变量的边际分布 在训练集合上的似然
- 实际上很难精确估计所有隐变量的后验概率,早期一般通过蒙特卡罗方法 MCMC 或变分方法来近似,但效率较低,从而导致其参数学习比较困难
为了更有效地训练深度信念网络,将每一层的 Sigmoid 信念网络转换为受限玻尔兹曼机
- 好处:隐变量的后验概率是互相独立的,从而可以很容易地采样
- 深度信念网络可以看作由多个受限玻尔兹曼机从下到上进行堆叠,第
层受限玻尔兹曼机的隐层作为第
层受限玻尔兹曼机的可观测层
- 由此,深度信念网络可以采用逐层训练的方式快速训练,从最底层开始,每次只训练一层,直到最后一层
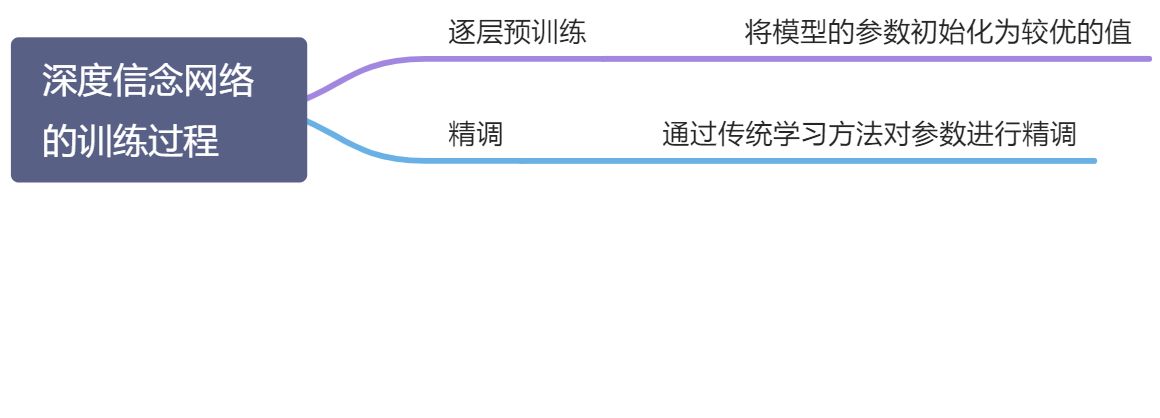
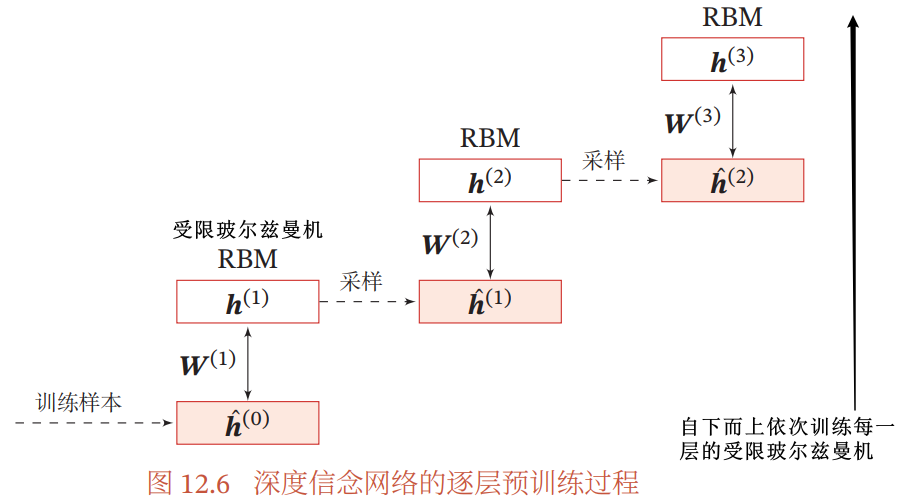
12.3.2.1 逐层预训练
逐层预训练:采用自下而上逐层训练的方式,将深度信念网络的训练简化为对多个受限玻尔兹曼机的训练
- 逐层预训练可以产生非常好的参数初始值,从而极大地降低了模型的学习难度

12.3.2.2 精调
精调 Fine-Tuning:经过与训练后,再结合具体的任务(监督 or 无监督学习),通过传统的全局学习算法对网络进行精调,使模型收敛到更好的局部最优点
作为生成模型的精调:
除了顶层的受限玻尔兹曼机,其它层之间的权重可以被分成:
- 向下的生成权重
:用来定义原始的生成模型
- 向上的认知权重
:用来计算反向(上行)的条件概率,初始
Contrastive Wake-Sleep 算法:
- Wake 阶段:
- 认知过程:通过外界输入(可观测变量)和向上的认知权重,计算每一层变量的上行的条件概率
并采样
- 修改下行的生成权重使得每一层变量的下行条件概率
最大
- 即,“如果现实和我想象的不一样,就改变我的生成权重使我想象的东西就是这样的”
- 认知过程:通过外界输入(可观测变量)和向上的认知权重,计算每一层变量的上行的条件概率
- Sleep 阶段:
- 生成过程:运行顶层的受限玻尔兹曼机,并在达到热平衡时采样,然后通过向下的生成权重逐层计算每一层变量的下行的条件概率
并采样
- 修改上行的认知权重使得每一层变量的上行条件概率
最大
- 即,“如果梦中的景象不是我脑中的相应概念,就改变我的认知权重使得这种景象在我看来就是这个概念”
- 生成过程:运行顶层的受限玻尔兹曼机,并在达到热平衡时采样,然后通过向下的生成权重逐层计算每一层变量的下行的条件概率
- 交替进行 Wake 和 Sleep 过程,直到收敛
作为判别模型的精调:
深度信念网络的一个应用是作为深度神经网络的预训练模型,提供神经网络的初始权重
- 这时只需要向上的认知权重,作为判别模型使用
- 优点:预训练获得的权重在权值空间中比随即权重更接近最优的权重,避免了反向传播算法因随机初始化权值参数而陷入局部最优和训练时间长的缺点,提升了模型的性能,也加快了调优阶段的收敛速度
精调过程:在深度信念网络的最顶层再增加一层输出层,然后使用反向传播算法对这些权重进行调优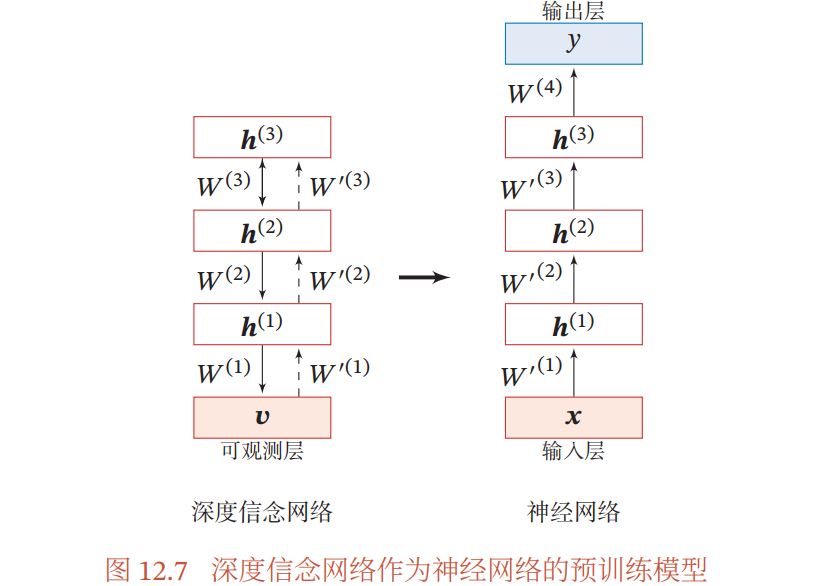
12.4 总结和深入阅读
玻尔兹曼机:是 Hopfield 网络的随机化版本,能够学习数据的内部表示,并且其参数学习的方式和赫布学习(人脑神经网络的学习方式)十分类似
- 缺点:没有任何约束的玻尔兹曼机因为过于复杂,难以应用在实际问题上
受限玻尔兹曼机:通过引入一定的约束(即变为二分图),受限玻尔兹曼机在特征抽取、协同过滤、分类等多个任务上得到了广泛应用
- 对比散度算法使得受限玻尔兹曼机的训练非常高效
- 受限玻尔兹曼机作为深度信念网络的一部分,显著提高了语音识别的精度,并开启了深度学习的浪潮
深度信念网络:可以通过逐层训练和精调有效的学习
- 贡献:可以为一个深度神经网络提供较好的初始参数,从而使得训练深度神经网络变得可行
- 除了深度信念网络,自编码器、稀疏自编码器、去噪自编码器等也可以用来作为深度神经网络的参数初始化,并得到和深度信念网络类似的效果
- 现在,出现了很多更加便捷的训练深度神经网络的技术,eg. ReLU 激活函数、权重初始化、逐层归一化以及残差连接等,使得我们可以不需要预训练就能训练出一个非常深的神经网络,因此深度信念网络作为一种深度学习模型已经很少使用
习题
习题 12-1 如果使用Metropolis算法对玻尔兹曼机进行采样,给出其提议分布的具体形式
习题 12-2 在受限玻尔兹曼机中,证明公式(12.47)
习题 12-3 在受限玻尔兹曼机中,证明公式(12.51)、公式(12.52)和公式(12.53)中参数的梯度
习题 12-4 计算“高斯-伯努利”受限玻尔兹曼机和“伯努利-高斯”受限玻尔兹曼机的条件概率𝑝(𝒗 = 1|𝒉)和𝑝(𝒉 = 1|𝒗)
习题 12-5 在受限玻尔兹曼机中,如果可观测变量服从多项分布,隐变量服务伯努利分布,可观测变量
的条件概率为
,其中𝑘 ∈ [1, 𝐾]为可观测变量的取值,
和
为参数,请给出满足这个条件分布的能量函数
习题 12-6 在深度信念网络中,试分析逐层训练背后的理论依据
习题 12-7 分析深度信念网络和深度玻尔兹曼机之间的异同点