Wasserstein distance
不同域内任意两假设的输出差异
定义 #card=math&code=%5Cepsilon%7BT%7D%5Cleft%28h%2C%20h%5E%7B%5Cprime%7D%5Cright%29) 是两个假设在域 T 上的输出差异,即:%2C%20h%5E%7B%5Cprime%7D(x))#card=math&code=l_%7Bh%2C%20h%5E%7B%5Cprime%7D%7D%3A%20x%20%5Clongrightarrow%20l%28h%28x%29%2C%20h%5E%7B%5Cprime%7D%28x%29%29) 的期望。
满足一定条件下,任意两个假设在不同的域 S、T 上的输出差异被两个域内数据的 Wasserstein distance 给限制:
%20%5Cleq%20%5Cepsilon%7BS%7D%5Cleft(h%2C%20h%5E%7B%5Cprime%7D%5Cright)%2BW%7B1%7D%5Cleft(%5Cmu%7BS%7D%2C%20%5Cmu%7BT%7D%5Cright)%0A#card=math&code=%5Cepsilon%7BT%7D%5Cleft%28h%2C%20h%5E%7B%5Cprime%7D%5Cright%29%20%5Cleq%20%5Cepsilon%7BS%7D%5Cleft%28h%2C%20h%5E%7B%5Cprime%7D%5Cright%29%2BW%7B1%7D%5Cleft%28%5Cmu%7BS%7D%2C%20%5Cmu_%7BT%7D%5Cright%29%0A)

使用有限样本估计的分布与真实分布之间的差异
当使用有限的个样本估计某个域的数据分布,得到概率测度
与真实概率测度
之间的差异的 Wasserstein distance 超过
的概率不超过
#card=math&code=%5Cexp%20%5Cleft%28-%5Cfrac%7B%5Cvarsigma%5E%7B%5Cprime%7D%7D%7B2%7D%20N%20%5Cvarepsilon%5E%7B2%7D%5Cright%29)。

源域与目标域性能差异上界
利用源域与目标域的有限样本,可以得到源域与目标域之间错误率之间的关系。
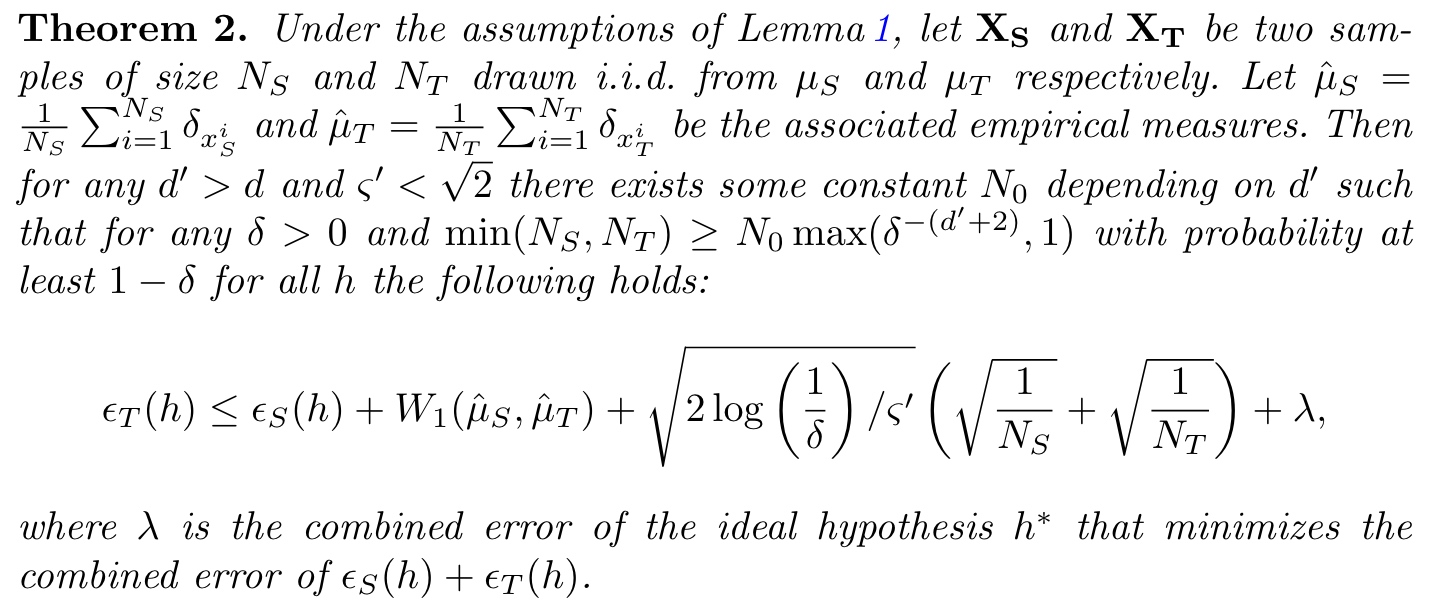
使用这一系列理论启发算法设计时,由于 Wasserstein distance 较难计算,通常在维度较低或假设数据分布服从高斯分布时才可以利用。
可用性质
Wasserstein distance 是一种真正的距离度量,因此满足三角不等式:%20%5Cleq%20W_1(x%2Cm)%20%2B%20W_1(m%2C%20y)#card=math&code=W_1%28x%2C%20y%29%20%5Cleq%20W_1%28x%2Cm%29%20%2B%20W_1%28m%2C%20y%29)。

