Highlights
近期出现了许多篇关于 Weakly-Supervised Contrastive Learning 相关的文章[1-2],文章的名字里将弱监督与表示学习(对比学习)相结合。其动机依旧是通过无监督的方式学习一套良好的表示,希望能够广泛应用到下游任务中。创新点在于在学习的过程中通过数据自身的相似性[1]或可获得的额外信息[2]产生弱监督标记帮助模型学习。
选择被 ICLR 和 ICCV 收录的两篇弱监督对比学习文章进行了快速阅读,发现这两篇文章殊途同归,共同指明了一条可以进一步提升对比学习性能的可行之路。
Details
Weakly Supervised Contrastive Learning[1]
本文的动机
传统对比学习在样本级别进行操作,使样本及其增广靠近,不同样本或其对应增广之间拉远(即优化损失函数 %20%2F%20%5Ctau%5Cright)%7D%7B%5Csum%7Bk%3D1%7D%5E%7BN%7D%20%5Cmathbb%7B1%7D%7B%5Bk%20%5Cneq%20i%5D%7D%20%5Cexp%20%5Cleft(%5Coperatorname%7Bsim%7D%5Cleft(%5Cmathbf%7Bz%7D%7Bi%7D%2C%20%5Cmathbf%7Bz%7D%7Bk%7D%5Cright)%20%2F%20%5Ctau%5Cright)%7D#card=math&code=%5Cmathcal%7BL%7D%7BN%20C%20E%7D%3D-%5Clog%20%5Cfrac%7B%5Cexp%20%5Cleft%28%5Coperatorname%7Bsim%7D%5Cleft%28%5Cmathbf%7Bz%7D%7Bi%7D%2C%20%5Cmathbf%7Bz%7D%7Bj%7D%5Cright%29%20%2F%20%5Ctau%5Cright%29%7D%7B%5Csum%7Bk%3D1%7D%5E%7BN%7D%20%5Cmathbb%7B1%7D%7B%5Bk%20%5Cneq%20i%5D%7D%20%5Cexp%20%5Cleft%28%5Coperatorname%7Bsim%7D%5Cleft%28%5Cmathbf%7Bz%7D%7Bi%7D%2C%20%5Cmathbf%7Bz%7D_%7Bk%7D%5Cright%29%20%2F%20%5Ctau%5Cright%29%7D&id=OtNUs),其中
为正样本对)。但是这样做会使不同但相似样本之间也被拉远(这些样本在下游任务中本应数据同一个类别),从而造成类别碰撞问题(Class Collision)。
因此,本文在对比学习的过程中,利用基于图的方法动态发现相似的样本对。在学习过程中,使相似样本对之间也拉近,不相似样本对间才推远,从而解决类别碰撞的问题。
Weakly Supervision
本文基于所学样本的表示 ,生成一张最邻近图(即每个样本都与自己最相似的样本连一条双向边),然后跑一遍联通块标记算法(Connected Components Labeling),最终得到若干个联通块。在此,认为每个联通块内的样本都是相似的,持有共同的伪标记。
在获得联通块的基础上,计算弱监督标记指导的对比学习损失。针对每个联通块对比学习损失为:%20%2F%20%5Ctau%5Cright)%7D%7B%5Csum%7Bk%3D1%7D%5E%7BN%7D%20%5Cmathbb%7B1%7D%7B%5Bk%20%5Cneq%20i%5D%7D%20%5Cexp%20%5Cleft(%5Coperatorname%7Bsim%7D%5Cleft(%5Cmathbf%7Bv%7D%7Bi%7D%2C%20%5Cmathbf%7Bv%7D%7Bk%7D%5Cright)%20%2F%20%5Ctau%5Cright)%7D#card=math&code=%5Cmathcal%7BL%7D%7Bs%20u%20p%7D%5E%7Bi%7D%3D-%5Csum%7Bj%7D%5E%7BN%7D%20%5Cmathbb%7B1%7D%7B%5Cmathbf%7By%7D%7Bi%20j%7D%3D1%7D%20%5Clog%20%5Cfrac%7B%5Cexp%20%5Cleft%28%5Coperatorname%7Bsim%7D%5Cleft%28%5Cmathbf%7Bv%7D%7Bi%7D%2C%20%5Cmathbf%7Bv%7D%7Bj%7D%5Cright%29%20%2F%20%5Ctau%5Cright%29%7D%7B%5Csum%7Bk%3D1%7D%5E%7BN%7D%20%5Cmathbb%7B1%7D%7B%5Bk%20%5Cneq%20i%5D%7D%20%5Cexp%20%5Cleft%28%5Coperatorname%7Bsim%7D%5Cleft%28%5Cmathbf%7Bv%7D%7Bi%7D%2C%20%5Cmathbf%7Bv%7D%7Bk%7D%5Cright%29%20%2F%20%5Ctau%5Cright%29%7D&id=cXVK1)。 这里拉近同一个联通块内样本的距离,推远不同联通块间样本的距离。
在实际操作中,本文增加两个操作让这一思路更加实用:
(1) 交换视图:在同一增广操作下,生成的联通块内样本相似度本身就高,因此基于联通块计算出来的对比学习损失很小。本文,通过交换生成的联通图来解决这个问题,即在A增广下生成联通图GA,在B增广下生成联通图GB,然后用GA指导B增广的表示,GB指导A增广的表示。
(2) 双头网络:本文保留传统对比学习损失,在特征表示上额外增加一个网络头用于计算基于联通块的对比学习损失。这样,模型既能够从原始(基于样本的)对比学习中获益,也可以从基于联通块的对比学习中获益。
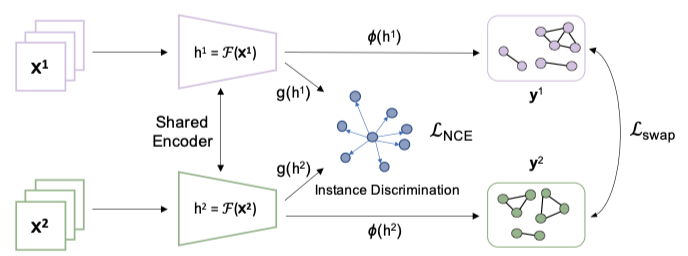
本文所提对比学习框架如下图所示,同一样本以方式进行增广后得到 ,再经过特征提取器得到其表示
。后续接一个双头网络
%2C%20%5Cphi(%5Ccdot)#card=math&code=g%28%5Ccdot%29%2C%20%5Cphi%28%5Ccdot%29&id=wYju8),其中
#card=math&code=g%28%5Ccdot%29&id=NZ6qm) 对应传统的对比学习损失,
#card=math&code=%5Cphi%28%5Ccdot%29&id=NdPHu) 对应基于相似样本的对比学习损失。
Multi-Crops
因此本文从样本相似度的角度入手,所以很自然地将 Multi-Crops 操作利用相似样本进行了扩展。
原始的 Multi-Crops 操作,利用对原图的随机裁切生成原图正样本以扩充正样本对在总体样本对中的数量。在本文中,通过构建样本的KNN图,寻找样本的K个相似样本作为正样本对,如此同样能够扩充正样本对的比例,同时正样本对的信息量更加丰富了。
Learning Weakly-supervised Contrastive Representations[2]
本文的动机
本文从实际应用的角度出发,考虑在收集样本的同时也能收集到一些与样本相关的信息,例如:图片中可能包含一些地域、内容的元信息,能够为表示学习带来额外的信息。如何能够将这些信息有效的利用,从而学习得到一个更有区分能力的表示是一个有价值的问题。
本文的方法
本文的思路比较简单,通过对额外能够获得的信息进行聚类,生成能够指导样本学习的弱监督信息,然后进行基于聚类的对比学习:
%20%5Csim%20%5Cmathbb%7BE%7D%7Bz%20%5Csim%20P%7BZ%7D%7D%7D%5Cleft%5BP%7BX%20%5Cmid%20z%7D%20P%7BY%20%5Cmid%20z%7D%5Cright%5D%5E%7B%5Cotimes%20n%7D%5Cleft%5B%5Cfrac%7B1%7D%7Bn%7D%20%5Csum%7Bi%3D1%7D%5E%7Bn%7D%20%5Clog%20%5Cfrac%7Be%5E%7Bf%5Cleft(x%7Bi%7D%2C%20y%7Bi%7D%5Cright)%7D%7D%7B%5Cfrac%7B1%7D%7Bn%7D%20%5Csum%7Bj%3D1%7D%5E%7Bn%7D%20e%5E%7Bf%5Cleft(x%7Bi%7D%2C%20y%7Bj%7D%5Cright)%7D%7D%5Cright%5D%0A#card=math&code=%5Cmathrm%7BCl%7D-%5Coperatorname%7BInfoNCE%7D%3D%5Csup%20%7Bf%7D%20%5Cmathbb%7BE%7D%7B%5Cleft%28x%7Bi%7D%2C%20y%7Bi%7D%5Cright%29%20%5Csim%20%5Cmathbb%7BE%7D%7Bz%20%5Csim%20P%7BZ%7D%7D%7D%5Cleft%5BP%7BX%20%5Cmid%20z%7D%20P%7BY%20%5Cmid%20z%7D%5Cright%5D%5E%7B%5Cotimes%20n%7D%5Cleft%5B%5Cfrac%7B1%7D%7Bn%7D%20%5Csum%7Bi%3D1%7D%5E%7Bn%7D%20%5Clog%20%5Cfrac%7Be%5E%7Bf%5Cleft%28x%7Bi%7D%2C%20y%7Bi%7D%5Cright%29%7D%7D%7B%5Cfrac%7B1%7D%7Bn%7D%20%5Csum%7Bj%3D1%7D%5E%7Bn%7D%20e%5E%7Bf%5Cleft%28x%7Bi%7D%2C%20y%7Bj%7D%5Cright%29%7D%7D%5Cright%5D%0A&id=hHtIm)
假设通过额外的信息得到了 个类,拉近每个聚类内样本
的距离,拉远属于不同聚类的样本
间的距离。
当聚类等于标记时,此对比学习损失等价于监督对比学习损失,当聚类大小为 1 时,此对比学习损失等与普通的对比学习损失。因此,这种基于聚类的对比学习损失,可以看作是监督/普通对比学习损失的一种推广。
当没有样本的相关属性时,应该如何产生弱监督信息呢。本文提出了一种基于 K-Means 的方法,将样本聚类成若干类别后,指导模型的学习。利用一种类似 EM 的方法,学习特征 -> 利用特征聚类 -> 指导特征学习 -> 聚类 ……
数学启发
进一步的,从数学的角度得到了一些启发:
%20%5Cleq%20H(Z)%0A#card=math&code=%5Cmathrm%7BCl%7D-%5Coperatorname%7BInfoNCE%7D%20%5Cleq%20D%7B%5Cmathrm%7BKL%7D%7D%5Cleft%28%5Cmathbb%7BE%7D%7BP%7BZ%7D%7D%5Cleft%5BP%7BX%20%5Cmid%20Z%7D%20P%7BY%20%5Cmid%20Z%7D%5Cright%5D%20%5C%7C%20P%7BX%7D%20P_%7BY%7D%5Cright%29%20%5Cleq%20H%28Z%29%0A&id=i17vU)
当%3DH(Z%20%5Cmid%20Y)%3D0#card=math&code=H%28Z%20%5Cmid%20X%29%3DH%28Z%20%5Cmid%20Y%29%3D0&id=U3wA7)时取等号。也就是说基于聚类的对比学习损失的上界是 给定聚类后两个样本的条件边际分布 与 两个样本的边际分布之间的 KL 散度。当样本的表示中已经充分包含了聚类信息时,此损失项收敛。
这个结论是比较正常的,因为基于聚类的对比学习损失就是奔着聚类的结果去学习的。但是这也说明了,如果聚类信息和下游任务的标记接近时,所学得的表示就更好用。
因此,本文提出了两个简单的信息论指标:下游标记与聚类的互信息#card=math&code=I%28Z%3BT%29&id=HkgAB)、给定下游标记时聚类信息的条件熵
#card=math&code=H%28Z%7CT%29&id=mX82q)。
#card=math&code=I%28Z%3BT%29&id=GCtpg) 说明了下游标记与聚类之间的相关程度,当这个相关程度越高,利用这种聚类学习得到的表示就越适用于这个下游任务。
#card=math&code=H%28Z%7CT%29&id=q6Dvl) 说明了聚类信息在刻画下游标记时包含多少冗余信息,这些信息对于下游任务时无用的。
利用这两个指标,就可以估算出聚类与下游任务之间的关系,从而不用训练模型就可以估计此方法是否适用于下游任务。
文章在实验中对这两个指标进行了验证,随着聚类数量上升,互信息逐渐达到上界,条件熵逐渐也逐渐达到上界。这个实验的结果比较显然,只要属性与下游任务不冲突,这样的趋势是一定会达到的。
比较有意义的一个实验是,基于本文提出的 K-Mean 聚类 + 聚类对比学习算法,也能够获得比较好的性能,这说明在对比学习中动态的加入聚类确实能够较好地提升表示的性能。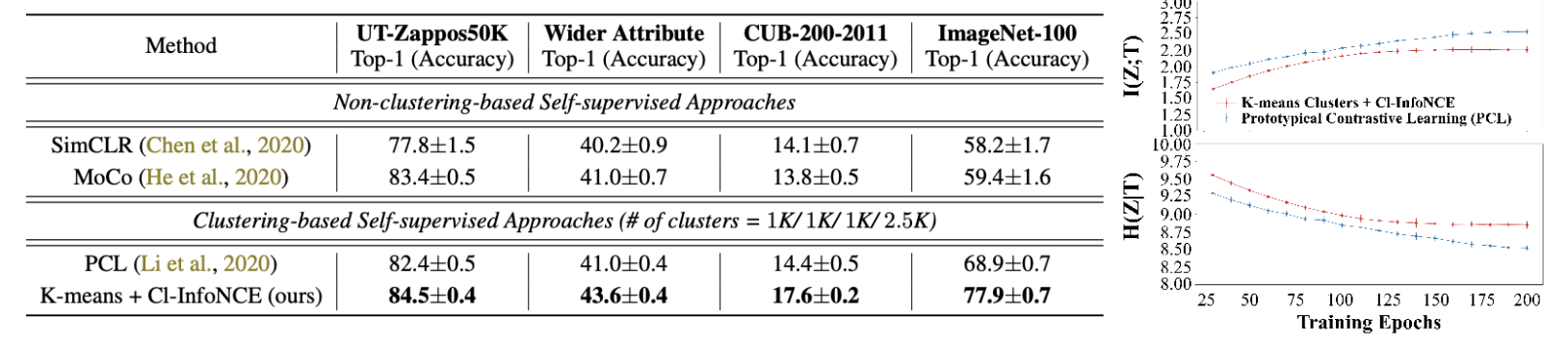
Conclusion
[1] 从对比学习中类别碰撞问题出发,[2] 从表示学习时额外可利用信息的角度出发,将传统对比学习损失改进为基于聚类的对比学习损失,从主要思路来看殊途同归。技术上,两篇文章获取聚类的方式也有所不同,[1] 利用样本间的局部邻接关系(1NN, KNN) 生成联通块(聚类),[2] 则直接利用 K-Means 聚类指导表示的学习,虽方式不同,但是证明了样本本身的相似性有利于提升对比学习性能。
[1] 为了使文章更为扎实,在此基础上进一步提出了很多技巧,将性能做到了极致。这可能也是 ICCV 会议特性使然。 [2] 则从数学角度提出了两个有一些参考价值的指标(互信息和条件熵),初步揭示了直觉上一致的聚类对比损失、普通对比损失、监督对比损失之间的关系。
Reference
[1] Mingkai Zheng, Fei Wang, Shan You, Chen Qian, Changshui Zhang, Xiaogang Wang, Chang Xu: Weakly Supervised Contrastive Learning. ICCV 2021
[2] Yao-Hung Hubert Tsai, Tianqin Li, Weixin Liu, Peiyuan Liao, Ruslan Salakhutdinov, Louis-Philippe Morency: Learning Weakly-supervised Contrastive Representations. ICLR 2021.

