No.142 环形链表②（Medium）

题目描述

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。注意，pos 仅仅是用于标识环的情况，并不会作为参数传递到函数中。

说明：不允许修改给定的链表。

进阶：

你是否可以使用 O(1) 空间解决此题？
示例：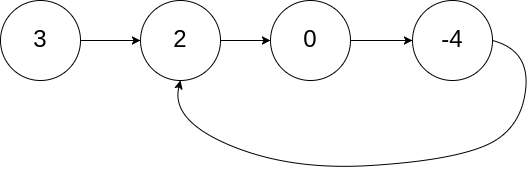

返回第二个结点

思路

该题和环形链表①的区别是：
环形链表①仅需要判断是否存在环，因此快慢指针如果相遇，就表示有环，返回true或者false即可。
环形链表②则需要找到环的结点，例如示例中的2结点为环的入口，因此返回该结点。

具体分析如下：

1. f 为 fast指针走过的路程， s为slow指针走过的路程，因为f的速度是s的两倍，因此固定有 f = 2s;
2. 设环之前的路程为a, 环的路程为b, 当fast指针和slow指针相遇时，有: f = s + nb, 即快指针比慢指针多走了nb的路程。
3. 根据1和2，得到s = nb以及f = 2s = 2nb；
4. 假设从头结点开始，走k步可以到达环的开始结点，那么k = a + nb, 结合3中的s = nb, 那么只需要s再走a步即可抵达环的开始结点；
5. 但是a是未知的，那我们假设一个结点从头结点出发，走a步抵达环的开始，同时slow结点也是走a步抵达环的开始，因此两个同时走，会在环的头结点相遇。返回相遇的结点就是题目要求的环的头结点。

从代码的角度来说：

1. 先找到快慢指针相遇的结点；
2. 然后令一个指针从head出发，同时和slow往后走，当slow和该指针相遇时，相遇的结点就是要求的环的开始结点。

代码

public class Solution {
    public ListNode detectCycle(ListNode head) {
        // 如果是空链表或者只有一个结点且不成环，直接返回Null
        if (head == null || head.next == null) {
            return null;
        }
        ListNode fast = head;
        ListNode slow = head;
        while (true) {
            // 如果无环，fast会先到链表尾部，只用判断fast即可
            // 如果无环，当存在奇数个结点时，fast必然会走到最后一个结点，那么fast.next == null 成立
            // 如果无环，当存在偶数个结点时，fast必然会走到null, 那么fast == null 成立
            if (fast == null || fast.next == null) {
                return null;
            }
             fast = fast.next.next;
            slow = slow.next;
            // 找到相遇的结点，代码如果能运行到此处，说明必然存在环，也必然相遇，必然可以break
            if (fast == slow) {
                break;
            }
        }
        ListNode temp = head;
        while (temp != slow) {
            temp = temp.next;
            slow = slow.next;
        }
        return temp;
    }
}

总结

可以看出，该题代码少，但是分析过程比较繁琐，因此记住两个关键点：

1. 找到快慢指针相遇结点。
2. 相遇后，一个指针从头部出发，slow接着走，相遇时的结点就是要返回的结点。