题目描述

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

示例1：

  1. 输入：s = "bbbab"
  2. 输出：4
  3. 解释：一个可能的最长回文子序列为 "bbbb" 。

示例2：

  1. 输入：s = "cbbd"
  2. 输出：2
  3. 解释：一个可能的最长回文子序列为 "bb" 。

思路

二维动态规划。

注意：
最长子序列和最长子串不一样，最长子序列可以是不连续的，而最长子串是连续的。

  1. dp的定义

dp[i][j]表示字符串s[i, i + 1, i + 2, … j]的最长回文子序列

  1. dp的初始化

对角线全是1。

  1. 状态转移方程
  • 如果s[i] == s[j], 那么字符i和字符j的加入能使dp[i + 1][j - 1] 增加2，例如：

a b c c a, 两端的两个a相等，那么dp[0][4] = dp[1][3] + 2;

  • 如果s[i] != s[j], 那么字符i和字符j不可能同时出现在最长回文序列中，那么：

dp[i][]j = Math.max(dp[i + 1][j], dp[i][j - 1]);

例如，对于：
a b c c ？

如果我们已知dp[0][3]为2， 现在将最后一个字符？添加进 a b c c, 有两种结果：

结果1： 添加进去的字符为d，对原来的最长回文子序列没有影响，那么dp[0][4] = dp[0][3] = 2
结果2：添加进去的字符为b，虽然s[0]和s[4]不相等，但是添加进去的字符b会影响dp[1][4]，即dp[0][4] = dp[1][4]，

那么最后到底取哪个呢？
取较大值即可，即dp[0][4] = Math.max(dp[0][3], dp[1][4])

以上状态转移方程用代码表示

  1. if (s.charAt[i] == s.charAt[j]) {
  2.     dp[i][j] = dp[i + 1][j - 1] + 2;
  3. } else {
  4.     dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]);
  5. }

我们根据状态转移方程来判断遍历方向：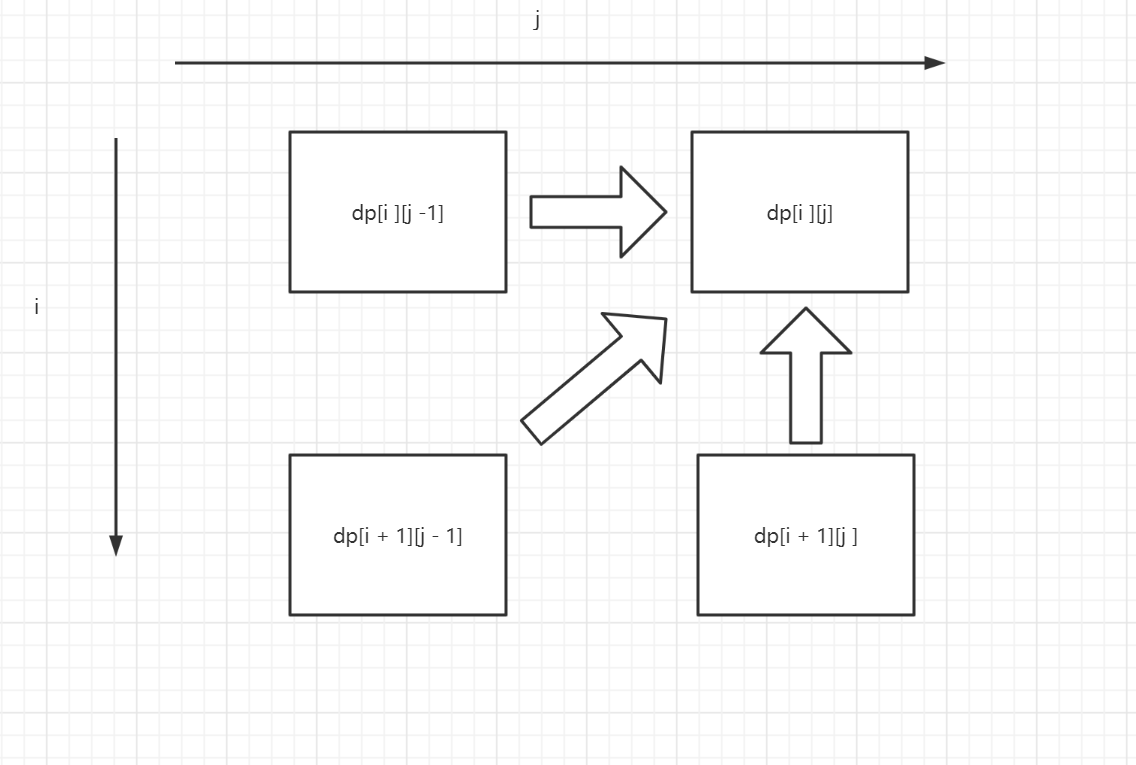
image.png

可以采用倒序的方式进行遍历，即：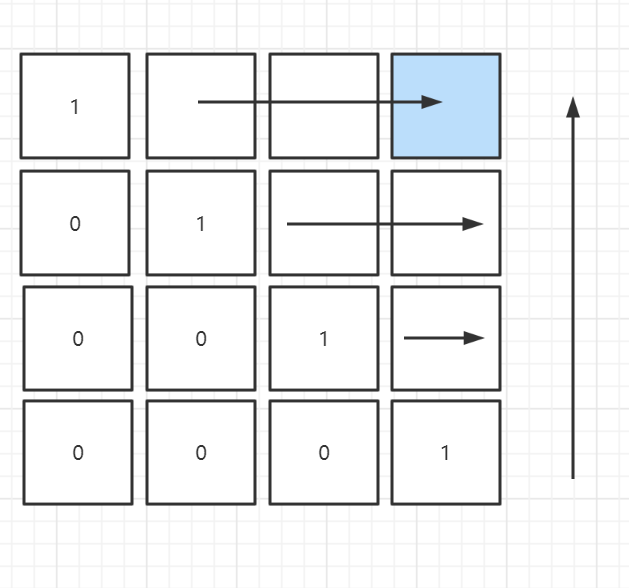
image.png

这样的遍历方式保证了，在求dp[i][j]时，dp[i + 1][j - 1]和dp[i][j - 1]和dp[i + 1][j]都是已知的。

最终代码：

  1. package redo;
  3. public class Solution_516 {
  4.     public int longestPalindromeSubseq(String s) {
  5.         int sLen = s.length();
  7.         int[][] dp = new int[sLen][sLen];
  9.         for (int i = 0; i < sLen; i++) {
  10.             dp[i][i] = 1;
  11.         }
  13.         for (int i = sLen - 2; i >= 0; i--) {
  14.             for (int j = i + 1; j < sLen; j++) {
  15.                 if (s.charAt(i) == s.charAt(j)) {
  16.                     dp[i][j] = dp[i + 1][j - 1] + 2;
  17.                 } else {
  18.                     dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]);
  19.                 }
  20.             }
  21.         }
  23.         return dp[0][sLen - 1];
  24.     }
  26.     public static void main(String[] args) {
  27.         String s = "aecda";
  28.         System.out.println(new Solution_516().longestPalindromeSubseq(s));
  29.     }
  30. }