No.96 不同的二叉搜索树 （Medium）

题目描述

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。
例如：n = 3
返回 5 。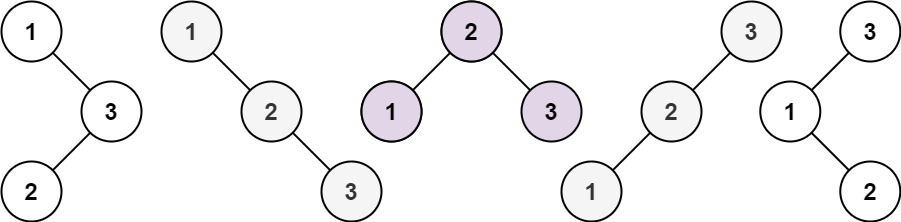

思路

什么是二叉搜索树？

即对于一个结点，其左子树的所有值都比该结点的值小，右子树的所有值都比该结点的值大。

什么是二叉排序树？

即二叉搜索树

为什么叫二叉搜索树？

因为便于搜索，例如查找n = 5, 从根结点开始查找，

1. 如果根结点等于5， 则直接返回。
2. 如果根结点小于5， 则去根结点的右子树去查找；
3. 如果根结点大于5，则去根结点的左子树去查找；
4. 重复2，3，直到找到n = 5 的结点

这道题怎么解？

思路：动态规划

令G(n)表示n个结点的二叉搜索树的数量，f(i)表示当根结点为i时的二叉搜索树的数量。
例如，G(10) 表示 n = 10时的二叉搜索树的总数，f(5)表示根结点为5时，二叉搜索树的数量。
那么可知：
G(n) = f (1) + f(2) + f(3) + … f(i) + … + f(n)
即G(10)为根结点为1，2，3 … 10时的二叉搜索树的数量总和。

那么f(i)怎么算呢？
拿f(5)来举例，i = 5。f(5)表示根结点为5时的二叉搜索树的数量，

• 那么根结点左子树包含的4（即 i - 1）个结点：1，2，3，4 （比5小）。 那么左子树形成的二叉搜索树的数量为 G(4)， 即G(i - 1)；
• 右子树包含5 （即n - i）个结点：6，7，8，9，10 （比5大）。那么右子树形成的二叉搜索树的数量为G(5)，即G(n - i);
• 那么总数量f(i) = G(i - 1) * G(n - i);

G(n)最后的表达：
G(n) = f(1) + f(2) + … + f(i) + … f(n)

代入f(i) = G(i - 1) * G(n - i)
G(n) =G(0) G(n - 1) + G(1) G(n - 2)+ G(2) G(n - 3) + … + G(n - 1) G(0)

例如：
G(4) = G(0) G(3) + G(1) G(2) + G(2) (1) + G(3) G(0)
G(5) = G(0) G(4) + G(1) G(3) + G(2) G(2) + G(3) G(1) + G(4) * G(0)

动态规划的初始值，即:
G(0) = 1; (0个结点时，空二叉搜索树，也是一棵树)
G(1) = 1; （1个结点时，唯一的一棵树）
G(2) = 2; (可以直接想象出来)，如果代入公式即：
G(2) = G(0) G(1) + G(1) G(0) = 1 + 1 = 2;

代码

class Solution {
    public int numTrees(int n) {
        // 初始化dp数组，默认dp[i] = 0
        // 长度为n + 1，例如想求n = 5, 那么需要数组长度为6, 因为存的是dp[0]到dp[5]
        int[] dp = new int[n + 1];
        // 初始化
        dp[0] = 1;
        dp[1] = 1;
        // 开始遍历，分别求dp[2], dp[3] ... dp[n]
        // 所以说从i = 2开始, i < n + 1即可以求出dp[n]，然后终止循环
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[j - 1] * dp[i - j];
                // 分析:
                // 初始值为0：
                // dp[2] = 0;
                // j = 1; j <= 2
                // dp[2] = dp[2] + dp[0] * dp[1] = dp[0] * dp[1]
                // j = 2; j <= 2
                // dp[2] = dp[2] + dp[1] * dp[0] = dp[0] * dp[1] + dp[1] * dp[0]
            }
        }
        return dp[n];
    }
}