No.98 验证二叉搜索树 (Medium)

题目描述

给定一个二叉树，判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

思路

二叉搜索树的中序遍历。

中序遍历：左 -> 根 -> 右。
对于二叉搜索树，有左 < 根 < 右。
因此对一棵二叉搜索树进行中序遍历，一定是递增的，例如：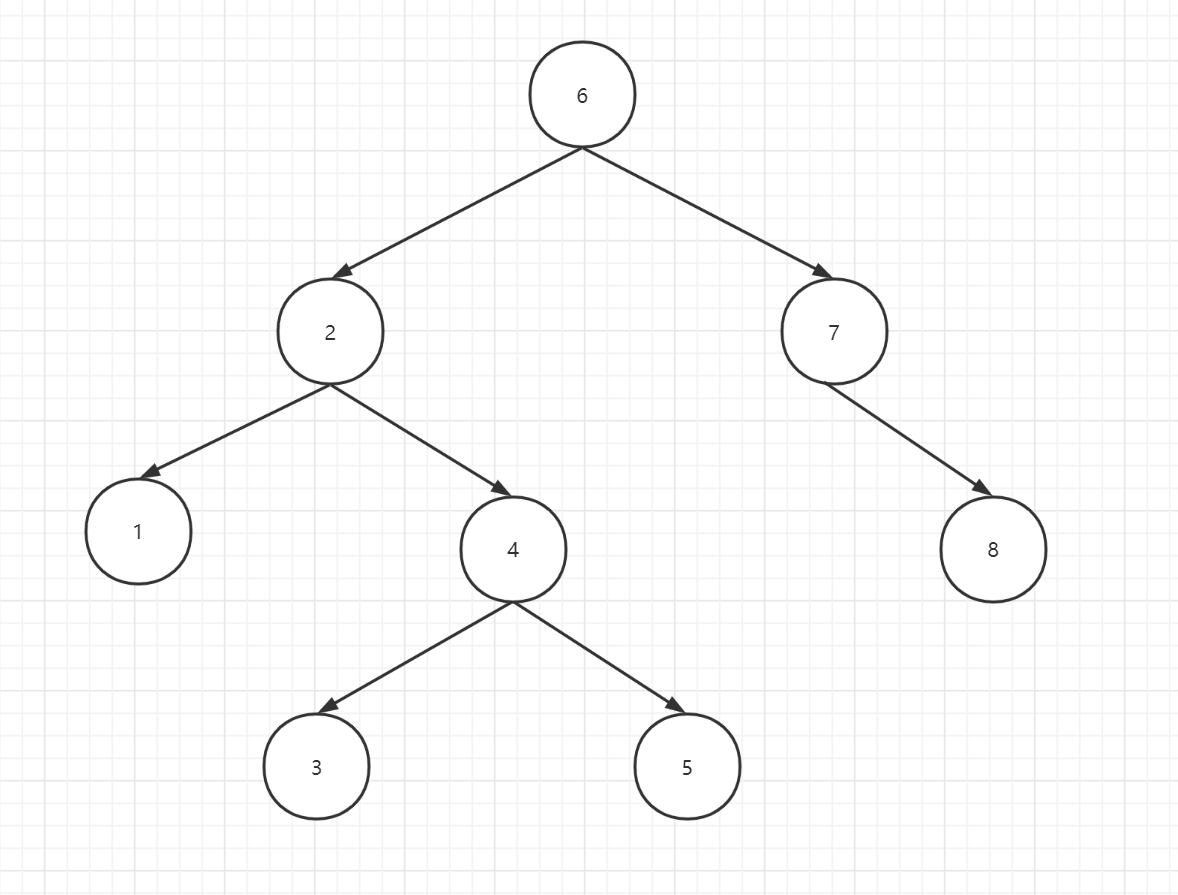

对如上二叉搜索树进行中序遍历，得到:
1, 2, 3, 4, 5, 6, 7, 8
因此我们对一棵二叉树进行中序遍历，如果发现当前遍历的结点的值小于上一个结点的值, 那么就不是一棵二叉搜索树。即如果：

1. 左不小于中， 或者
2. 中不小于右。

则不是二叉搜索树。

代码

回忆No.94, 采取递归实现中序遍历, 将其存放到一个数组中，遍历该数组，如果发现不是升序的则return false;

class Solution {
    public boolean isValidBST(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        traverse(root, result);
        // 判断结果数组是否递增
        for (int i = 0; i < result.size() - 1; i++) {
            if (result.get(i) >= result.get(i + 1)) {
                return false;
            }
        }
        return true;
    }
    // 与No.94完全相同
    private void traverse(TreeNode root, List<Integer> result) {
        if (root == null) {
            return;
        }
        traverse(root.left, result);
        result.add(root.val);
        traverse(root.right, result);
    }
}

以上方法可以被优化，实际上不用存放到数组中，而是在遍历过程中进行大小的判断。

class Solution {
    // 初始化前一个结点的值，默认为最小值，即最左边的结点先和最小值进行比较
    // 此处不用Integer.MIN_VALUE; 
    // 因为在Leetcode中有非常极端的条件，此处不用Integer.MIN_VALUE，
    // 需要让第一次比较为true, 所以采用Long.MIN_VALUE;
    long pre = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        boolean isValid = traverse(root);
        return isValid;
    }
    private boolean traverse(TreeNode root) {
        if (root == null) {
            return true;
        }
        if (!traverse(root.left)) {
            return false;
        }
        if (root.val <= pre) {
            return false;
        }
        pre = root.val;
        return traverse(root.right);
    }
}

TODO

对以上代码进行注释并详解。