力扣AC：最大回文数乘积

题目链接

最大回文数乘积

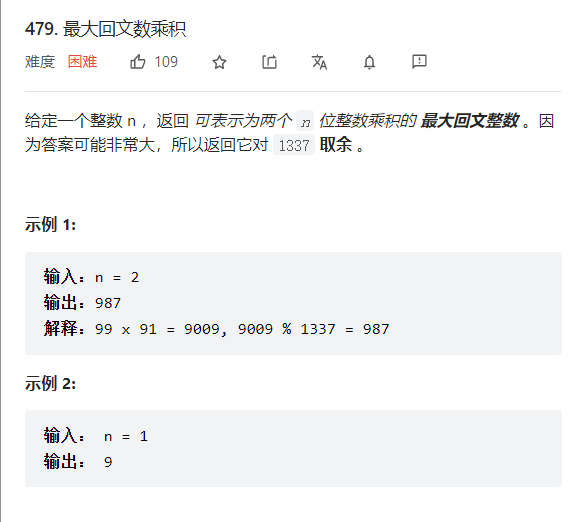
题目描述

实现代码

个人实现代码（超时）：

class Solution {
    public int largestPalindrome(int n) {
        int start = 1;
        int end = 9;
        for(int i=2; i<=n; i++) {
            start = start*10 + 1;
            end = end*10 + 9;
        }
        long result = 0;
        long longRes = 0;
        for(int i=end; i>=start; i--) {
            for(int j = end; j >= start ;j--) {
                longRes = i * j;
                if(isHuiwen(longRes)) {
                    result = result < longRes ? longRes : result;
                }
            }
        }
        return (int)(result % 1337);
    }
    private boolean isHuiwen(long x) {
        long temp = x % 10;
        long origin = x;
        x /= 10;
        if(temp == 0) {
            if(x > 0) {
                return false;
            }
            return true;
        }
        while(x != 0) {
            temp = temp * 10 + x % 10;
            x /= 10;
        }
        return temp == origin;
    }
}

参考官方思路：

1. 首先构造回文数；
2. 然后判断该回文数是否可以拆分为两个n位的数

思想原理：对于两个n位数的乘积，最大值的位数为2n;
实现代码：

class Solution {
    public int largestPalindrome(int n) {
        if (n == 1) {
            return 9;
        }
        int upper = (int) Math.pow(10, n) - 1;
        int ans = 0;
        for (int left = upper; ans == 0; --left) { // 枚举回文数的左半部分
            long p = left;
            for (int x = left; x > 0; x /= 10) {
                p = p * 10 + x % 10; // 翻转左半部分到其自身末尾，构造回文数 p
            }
            for (long x = upper; x * x >= p; --x) {
                if (p % x == 0) { // x 是 p 的因子
                    ans = (int) (p % 1337);
                    break;
                }
            }
        }
        return ans;
    }
}