最优化原理

不论过去状态和决策如何，对前面的决策所形成的状态而言，余下的决策必须构成最优策略。简单来说就是一个最优策略的子策略也必须是最优的，而所有子问题的局部最优解将导致整个问题的全局最优。如果一个问题能满足最优化原理，那么就称其具有最优子结构性质，就可以通过动态规划算法进行求解。

0/1背包

问题描述：对于一个背包，固定容量为C，现在有N个物品，每个物品都分别对应其数量和单个价值，编写算法实现找到最大价值的拿取策略。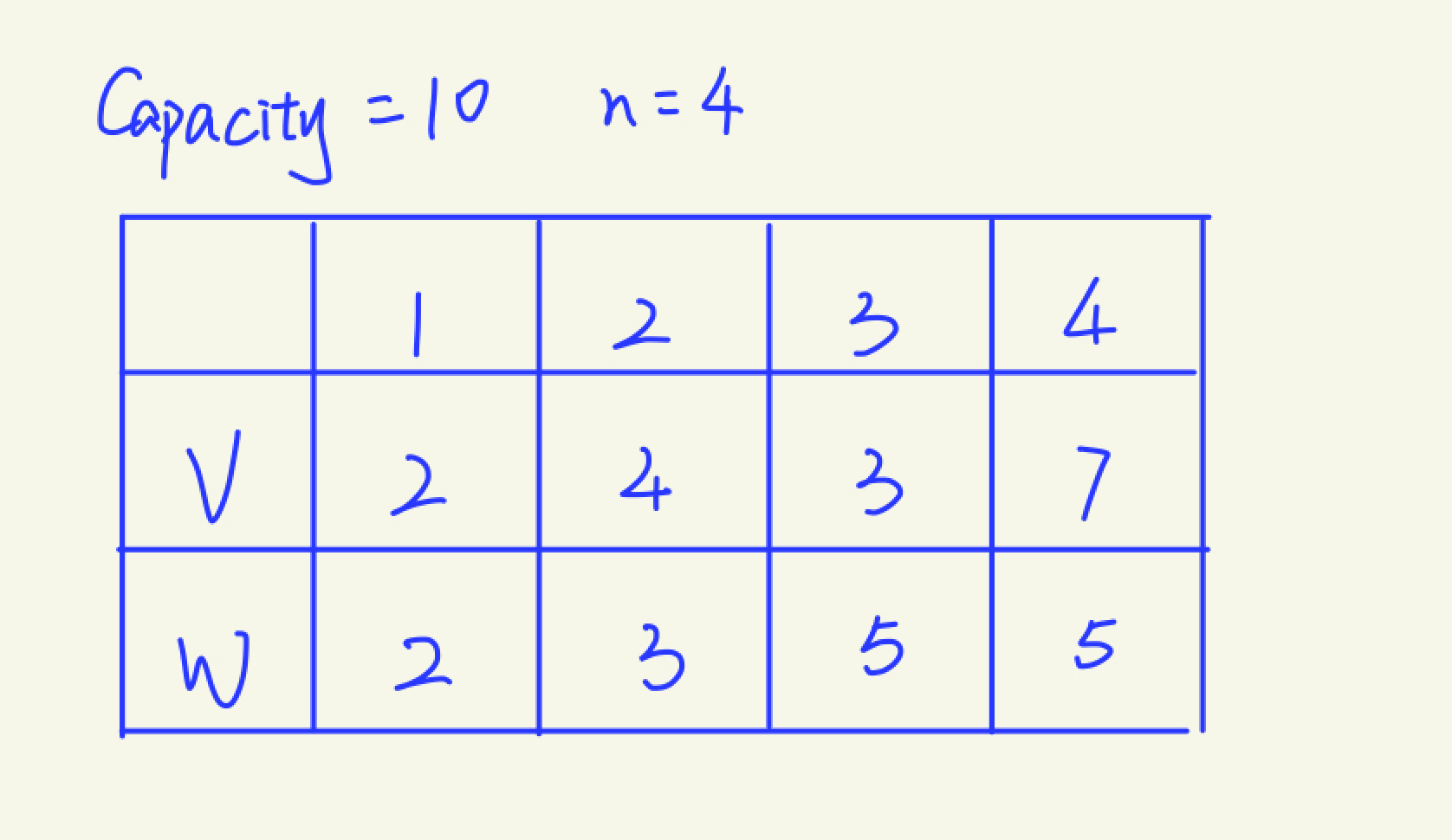
image.png

为什么叫0/1背包，是因为对于每个物品而言，只有两种选择，拿1或者不拿0；

首先，能快速想到的就是dfs，因为每个物品只有两个选择：拿或者不拿，所以针对这两个选择进行dfs遍历取价值最大的方案即可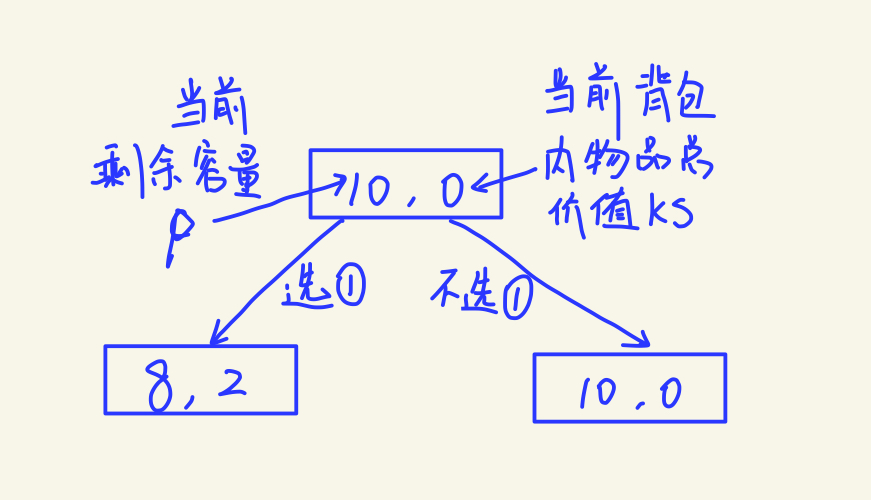
image.png

记数组dp[i][j]表示物品数量为i的情况下当背包容量为j能获取到的最大价值；可以得知dp[i][j]只与dp[i-1][j]有关，其状态转移方程为：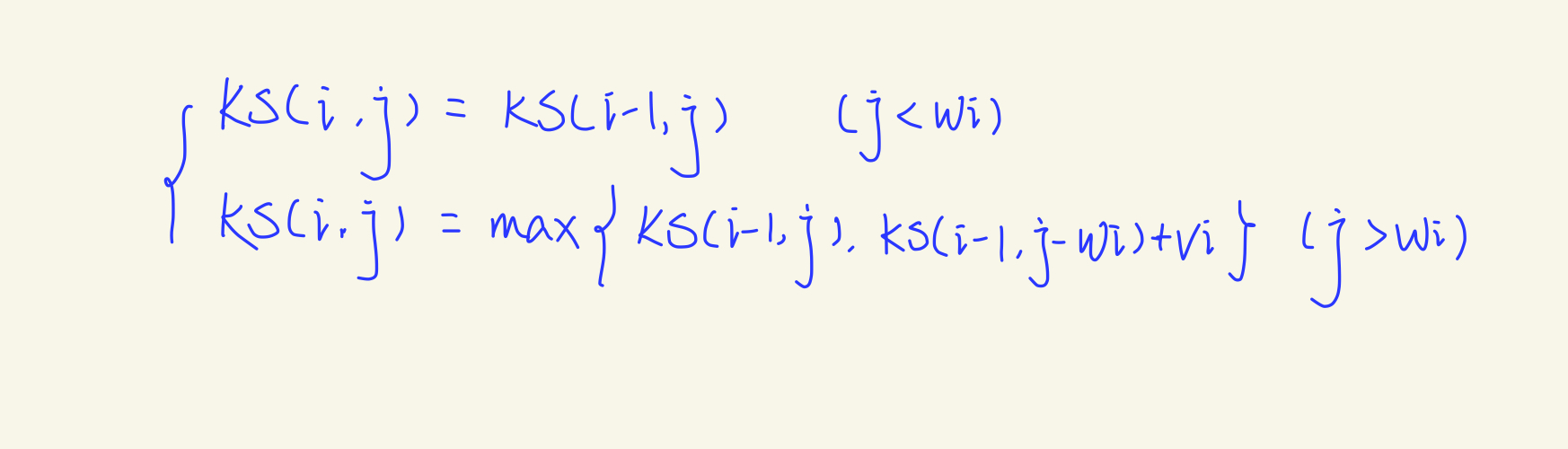
image.png
实现代码：

  1. public class Solution{
  2.     int[] vs = {0,2,4,3,7};
  3.     int[] ws = {0,2,3,5,5};
  4.     Integer[][] results = new Integer[5][11];
  6.     public static void main(String[] args) {
  7.         int result = new Solution().ks3(4,10);
  8.         System.out.println(result);
  9.     }
  11.     private int ks3(int i, int j){
  12.         // 初始化
  13.         for (int m = 0; m <= i; m++){
  14.             results[m][0] = 0;
  15.         }
  16.         for (int m = 0; m <= j; m++){
  17.             results[0][m] = 0;
  18.         }
  19.         // 开始填表
  20.         for (int m = 1; m <= i; m++){
  21.             for (int n = 1; n <= j; n++){
  22.                 if (n < ws[m]){
  23.                     results[m][n] = results[m-1][n];
  24.                     continue;
  25.                 }
  26.                 // 容量足够
  27.                 results[m][n] = Math.max(results[m-1][n], results[m-1][n-wx[m]] + vs[m]);
  28.             }
  29.         }
  30.         return results[i][j];
  31.     }
  32. }

完全背包

问题描述：有N种物品和一个容量为T的背包，每种物品都就可以选择任意多个，第i种物品的价值为P[i]，体积为V[i]，求解：选哪些物品放入背包，可卡因使得这些物品的价值最大，并且体积总和不超过背包容量。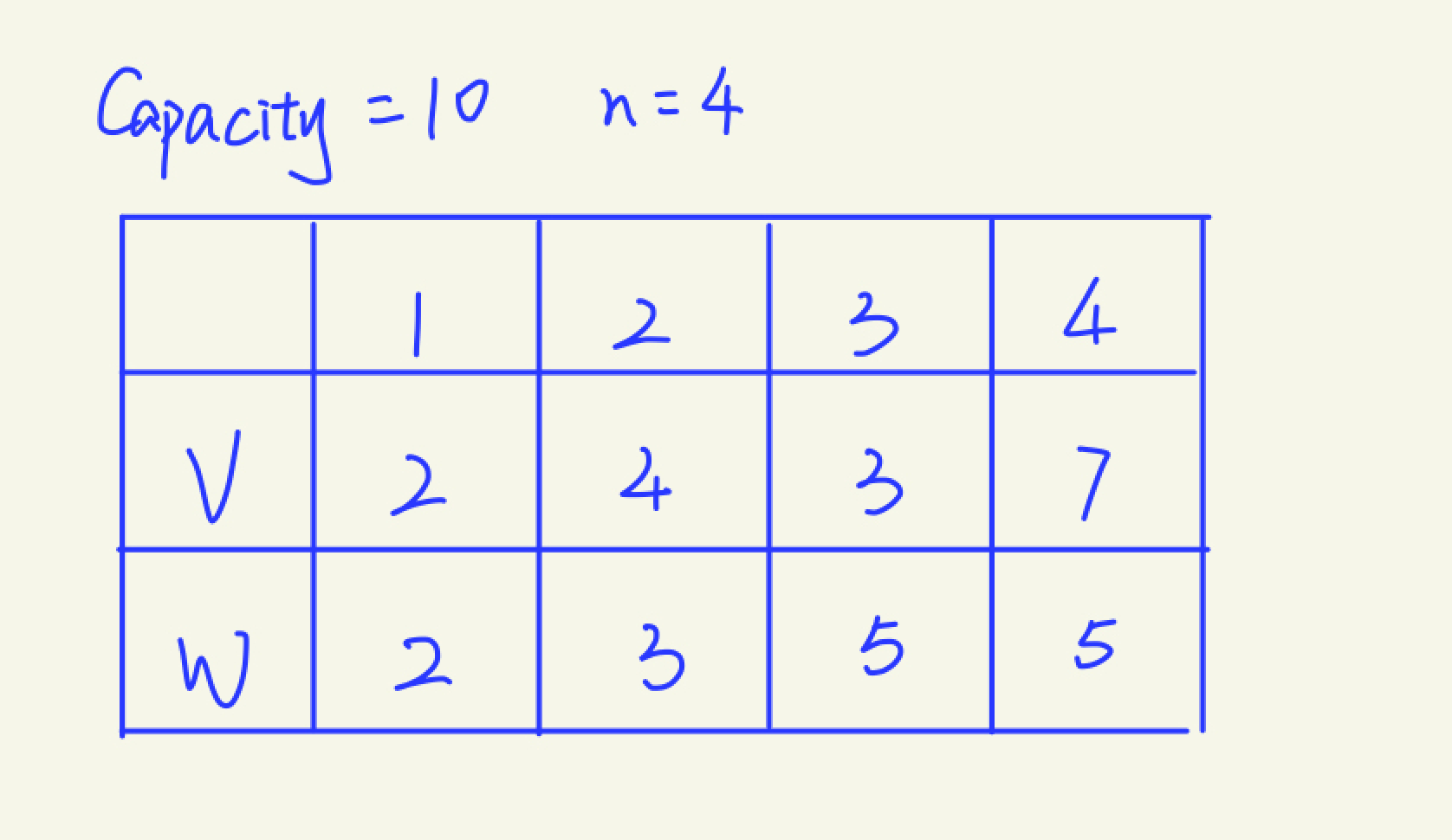
image.png

其思路跟0/1背包挺类似，区别就在于每个物品在容量允许的情况下可以拿多次，因此状态转移方程需要进行改变；

记dp[i][j]表示前i个物品在容量为j的情况下的最大价值，则dp[i][j]的价值同样只与dp[i-1][j]有关，区别在于每次需要跟取0个或者多个第i个物品时的价值进行比较，其状态转移方程如下：

ks(i,t) = max{ks(i-1, t - V[i] k) + P[i] k}; （0 <= k * V[i] <= t）

实现代码：

  1. public static class Demo {
  3.     private static int[] P={0,5,8};
  4.     private static int[] V={0,5,7};
  5.     private static int T = 10;
  7.     public static void main(String[] args) {
  8.         int result = new Demo().ks(P.length - 1,10);
  9.         System.out.println("最大价值为：" + result);
  10.     }
  12.     private int ks(int i, int t){
  13.         int result = 0;
  14.         if (i == 0 || t == 0){
  15.             // 初始条件
  16.             result = 0;
  17.         } else if(V[i] > t){
  18.             // 装不下该珠宝
  19.             result = ks(i-1, t);
  20.         } else {
  21.             // 可以装下
  22.             // 取k个物品i，取其中使得总价值最大的k
  23.             for (int k = 0; k * V[i] <= t; k++){
  24.                 int tmp2 = ks(i-1, t - V[i] * k) + P[i] * k;
  25.                 if (tmp2 > result){
  26.                     result = tmp2;
  27.                 }
  28.             }
  29.         }
  30.         return result;
  31.     }
  32. }

参考文章

三种背包问题解答