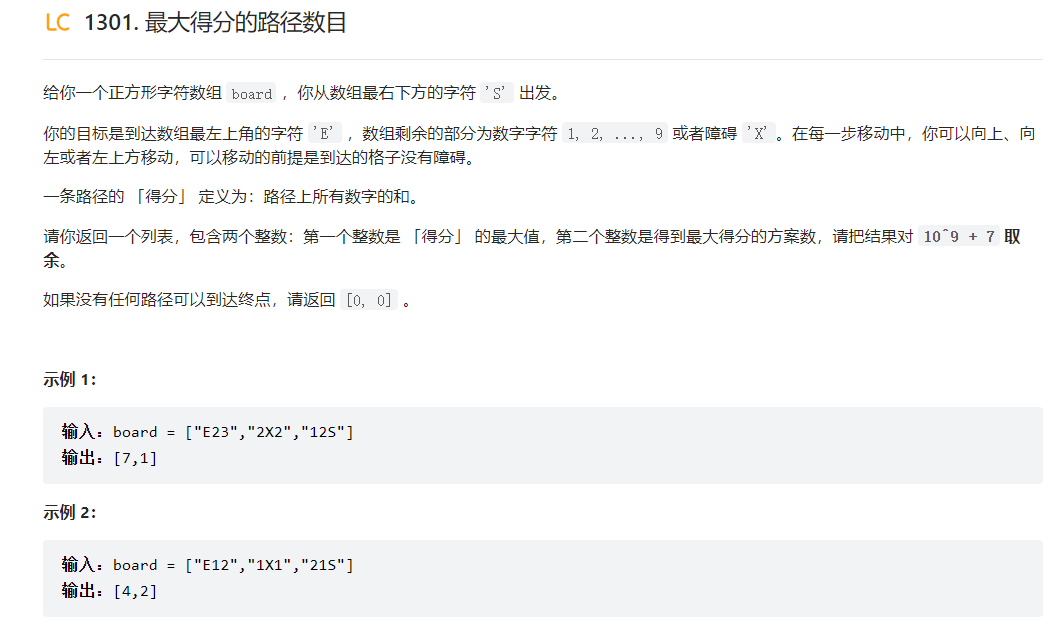
题目链接

最大得分的路径数目

题目描述

image.png

实现代码

dfs递归遍历实现代码：（超时）

  1. class Solution {
  3.     int max = 0;
  5.     int count = 0;
  7.     public int[] pathsWithMaxScore(List<String> board) {
  9.         int n = board.size();
  10.         int[][] arr = new int[n][n];
  12.         for (int i = 0; i < n; i++) {
  13.             String str = board.get(i);
  14.             for (int j = 0; j < n; j++) {
  15.                 char c = str.charAt(j);
  16.                 if(c >= '0' && c <= '9') {
  17.                     arr[i][j] = c - '0';
  18.                 } else if(c == 'S'){
  19.                     arr[i][j] = 0;
  20.                 } else {
  21.                     arr[i][j] = Integer.MAX_VALUE;
  22.                 }
  23.             }
  24.         }
  26.         dfs(arr, n, n - 1, n - 1, 0);
  28.         return new int[]{max, count};
  29.     }
  31.     private void dfs(int[][] arr, int n, int curX, int curY, int curMax) {
  33.         if (curX < 0 || curX > n - 1) {
  34.             return;
  35.         }
  36.         if (curY < 0 || curY > n - 1) {
  37.             return;
  38.         }
  40.         if (curX == 0 && curY == 0) {
  41.             if (curMax == max) {
  42.                 count++;
  43.             } else if (curMax > max) {
  44.                 max = curMax;
  45.                 count = 1;
  46.             }
  47.             return;
  48.         }
  50.         if(arr[curX][curY] == Integer.MAX_VALUE) {
  51.             return;
  52.         }
  54.         curMax += arr[curX][curY];
  55.         dfs(arr, n, curX-1, curY, curMax);
  56.         dfs(arr, n, curX, curY-1, curMax);
  57.         dfs(arr, n, curX-1, curY-1, curMax);
  58.     }
  59. }

动态规划思想：

  1. class Solution {
  2.     int INF = Integer.MIN_VALUE;
  3.     int mod = (int)1e9+7;
  4.     int n;
  5.     public int[] pathsWithMaxScore(List<String> board) {
  6.         n = board.size();
  8.         // 将 board 转存成二维数组
  9.         char[][] cs = new char[n][n];
  10.         for (int i = 0; i < n; i++) {
  11.             cs[i] = board.get(i).toCharArray();
  12.         }
  14.         // f(i) 代表从右下角到位置 i 的最大得分
  15.         int[] f = new int[n * n]; 
  16.         // f(i) 代表从右下角到位置 i 并取到最大得分的方案数量
  17.         int[] g = new int[n * n]; 
  18.         for (int i = n - 1; i >= 0; i--) {
  19.             for (int j = n - 1; j >= 0; j--) {
  20.                 int idx = getIdx(i, j);
  22.                 // 一个初始化的状态，如果是在最后一格（起点）：
  23.                 // g[idx] = 1 : 代表到达起点的路径只有一条，这样我们就有了一个「有效值」可以滚动下去
  24.                 // f[idx] = 0 : 代表在起点得分为 0
  25.                 if (i == n - 1 && j == n - 1) {
  26.                     g[idx] = 1;
  27.                     continue;
  28.                 }
  30.                 // 如果该位置是「障碍点」，那么对应状态为：
  31.                 // g[idx] = 0   : 「障碍点」不可访问，路径为 0
  32.                 // f[idx] = INF : 「障碍点」不可访问，得分为无效值
  33.                 if (cs[i][j] == 'X') {
  34.                     f[idx] = INF;
  35.                     continue;
  36.                 }
  38.                 // 如果是第一个格子（终点），这时候位置得分为 0
  39.                 int val = (i == 0 && j == 0) ? 0 : cs[i][j] - '0';
  41.                 // u 代表当前位置的「最大得分」；t 代表取得最大得分的「方案数」
  42.                 int u = INF, t = 0;
  44.                 // 如果「下方格子」合法，尝试从「下方格子」进行转移
  45.                 if (i + 1 < n) {    
  46.                     int cur = f[getIdx(i + 1, j)] + val;
  47.                     int cnt =  g[getIdx(i + 1, j)];
  48.                     int[] res = update(cur, cnt, u, t);
  49.                     u = res[0]; t = res[1];
  50.                 }
  52.                 // 如果「右边格子」合法，尝试从「右边格子」进行转移
  53.                 if (j + 1 < n) {
  54.                     int cur = f[getIdx(i, j + 1)] + val;
  55.                     int cnt = g[getIdx(i, j + 1)];
  56.                     int[] res = update(cur, cnt, u, t);
  57.                     u = res[0]; t = res[1];
  58.                 }
  60.                 // 如果「右下角格子」合法，尝试从「右下角格子」进行转移
  61.                 if (i + 1 < n && j + 1 < n) {
  62.                     int cur = f[getIdx(i + 1, j + 1)] + val;
  63.                     int cnt = g[getIdx(i + 1, j + 1)];
  64.                     int[] res = update(cur, cnt, u, t);
  65.                     u = res[0]; t = res[1];
  66.                 }
  68.                 // 更新 dp 值
  69.                 f[idx] = u < 0 ? INF : u;
  70.                 g[idx] = t;
  71.             }
  72.         }
  74.         // 构造答案
  75.         int[] ans = new int[2];
  76.         // 如果终点不可达（动规值为 INF）时，写入 0
  77.         ans[0] = f[getIdx(0, 0)] == INF ? 0 : f[getIdx(0, 0)];
  78.         // 如果终点不可达（动规值为 INF）时，写入 0
  79.         ans[1] = f[getIdx(0, 0)] == INF ? 0 : g[getIdx(0, 0)];
  80.         return ans;
  81.     }
  83.     // 更新 dp 值
  84.     int[] update(int cur, int cnt, int u, int t) {
  85.         // 起始答案为 [u, t] : u 为「最大得分」，t 为最大得分的「方案数」
  86.         int[] ans = new int[]{u, t};
  88.         // 如果当前值大于 u，更新「最大得分」和「方案数」
  89.         if (cur > u) {
  90.             ans[0] = cur;
  91.             ans[1] = cnt;
  93.         // 如果当前值等于 u，增加「方案数」
  94.         } else if (cur == u && cur != INF) {
  95.             ans[1] += cnt;
  96.         }
  98.         ans[1] %= mod;
  99.         return ans;
  100.     }
  102.     // 二维坐标 (x,y) 与 idx 的相互转换
  103.     int getIdx(int x, int y) {
  104.         return x * n + y;
  105.     }
  106.     int[] parseIdx(int idx) {
  107.         return new int[]{idx / n, idx % n};
  108.     }
  109. }

在动态规划的基础上对复杂度进行优化（使用结构体）：

  1. class Solution {
  2.     final int MOD = 1000000007;
  3.     public int[] pathsWithMaxScore(List<String> board) {
  4.         int n = board.size();
  5.         //将给的字符表转化成字符矩阵
  6.         char[][] map = new char[n][n];
  7.         for(int i = 0; i < n; i++){
  8.             map[i] = board.get(i).toCharArray();
  9.         }
  10.         //初始化边界条件都要为0
  11.         Info[][] f = new Info[2][n+1];
  12.         for(int i = 0; i <= n; i++){
  13.             f[0][i] = new Info(0,0);
  14.             f[1][i] = new Info(0,0);
  15.         }
  16.         int last = 0,now = 1;
  17.         for(int i = n-1;i >= 0; i--){
  18.             last = now;
  19.             now = 1 - now;
  20.             for(int j = n-1; j >= 0; j--){
  21.                 if(i == n-1 && j == n-1) {
  22.                     //将起始分数设为1是为区分围墙全面堵死情况
  23.                     // 因为在右，右下，下三块均为0，说明堵死，就是现在这一块有分数也不能加
  24.                     //但是起始点三块都0，必须区分，起始要加，其他情况不加
  25.                     f[now][j] = new Info(1,1);
  26.                 }else
  27.                 if(i == 0 && j == 0){
  28.                     f[now][j] = MaxInfo(f[last][j],f[last][j+1],f[now][j+1]);
  29.                 }else
  30.                 if(map[i][j] == 'X'){
  31.                     f[now][j] = new Info(0,0);
  32.                 }else{
  33.                     f[now][j] = MaxInfo(f[last][j],f[last][j+1],f[now][j+1]);
  34.                     f[now][j].maxScores  += (f[now][j].maxScores == 0 ) ? 0 :map[i][j] - '0';
  35.                 }
  36.             }
  37.         }
  38.         //如果最后结果不为0，也就是没有全面封死，要把起始1减掉
  39.         int maxScore = f[now][0].maxScores != 0 ? f[now][0].maxScores-1 : 0;
  40.         return new int[]{maxScore,f[now][0].maxways};
  42.     }
  43.     public Info MaxInfo(Info a,Info b,Info c){
  44.         int maxScore = 0;
  45.         int maxway = 0;
  46.         maxScore = Math.max(a.maxScores,Math.max(b.maxScores,c.maxScores));
  47.         if(maxScore == a.maxScores) maxway += a.maxways;
  48.         if(maxScore == b.maxScores) maxway += b.maxways;
  49.         if(maxScore == c.maxScores) maxway += c.maxways;
  50.         return new Info(maxScore % MOD,maxway % MOD);
  51.     }
  52.     class Info{
  53.         int maxScores;
  54.         int maxways;
  55.         public Info(int maxScores,int maxways){
  56.             this.maxScores = maxScores;
  57.             this.maxways = maxways;
  58.         }
  59.     }
  60. }